【BZOJ2115】Xor(线性基---求无向图1->n路径上最大的边权异或值--可出现环)

题目地址：https://www.lydsy.com/JudgeOnline/problem.php?id=2115

题目：

---

Description

Input

第一行包含两个整数N和 M， 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边，每行三个整数Si，Ti ，Di，表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。

Output

仅包含一个整数，表示最大的XOR和（十进制结果）,注意输出后加换行回车。

Sample Input

5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2

Sample Output

6

HINT

解题思路：

---

1e18，xor，当然是线性基啦( ´▽｀)

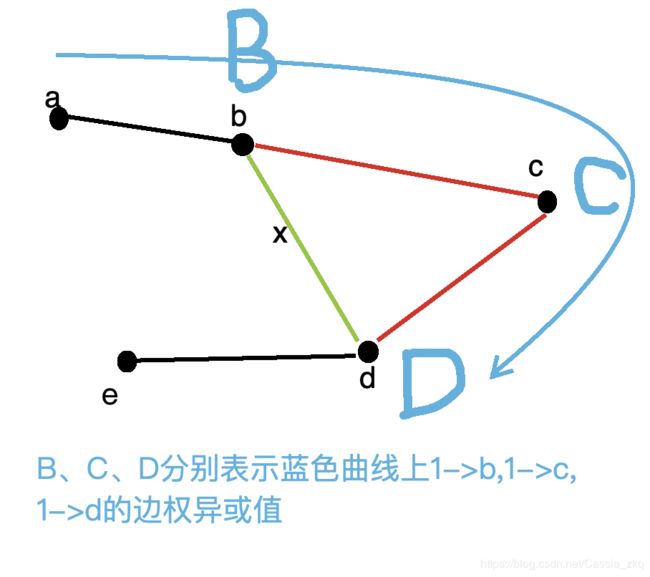
因为1->n的路径中可以出现环，所以有些边权会被重复异或，对于如下图：

在对图进行dfs遍历的时候，依次遍历到1->....->a->b->c->d

当d再向后遍历时：
(1)遍历到b，但是b已经访问了，因为本题的路径是允许出现环的，所以是允许在回到b的。但是此时不需要再更新1->b的边权异或值的，另开一个数组记录图中存在的环的异或值，上图中环的边权异或值为：，遍历与d相连的其他节点

(2)遍历到e，因为e没有被访问，通过e再进行dfs，同时更新1->e的边权异或值，当然这里1->n的边权异或值只对应某一条1->不出现环的路径

当遍历完整个图之后，用环值（环的边权异或值）构建线性基。

ans初始化为1->n的边权异或值，遍历线性基中非0的值p[j]，取max（ans，ans^p[j]）

思路的正确性证明：

因为这些环是在确定1->n的边权异或值时,通过dfs遍历这条路径上的点得到的，所以一定可以通过1->n路径上的某些点访问到这些环，这些环都是可达的。

这就意味着1->n的边权异或值 异或 图中的环得到的依旧是满足1到n的路径，只不过这条路径中某些边被重复访问了。不过我们不知道哪些环的边权异或值 异或 ans是最大的，所以我们通过这些边权异或值构建线性基，由线性基的各个值和ans异或并不断更新ans，确定最终的答案。

对于“解题思路”的第一个图，如果d的下一个节点是n,且1->n的边权异或值（ans的初值）是通过路径1->...->a->b->c->d->n确定的，在求最终结果时，当ans^图中环的边权异或值时，相当于得到就是1->...->a->b->d->n的边权异或值，这样就不用担心1->n的有些路径没有被访问到了。

注意：点最多有5e4个，但是图中的环不只5e4，可以把存环的数组定义为5e5+100大小，或者用vector<>存

不一定环边权异或值们能得到的最大异或值和ans进行异或所得到的就是最大的ans，本题要用普通的线性基，动态更新ans

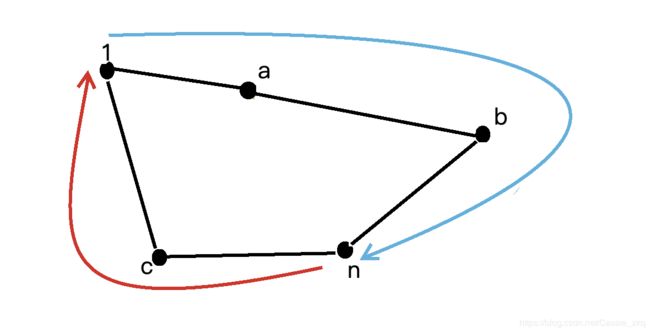
写完之后突然发现这个例子好像并没有意义，暂且留着吧，可以跳过@(・●・)@

若一个完整的图如下：

1->a->b->n这条蓝色的路径确定的1->n的边权异或值，且这个值只有不会被更新,ans初始化为这个值

n向后遍历，n->c->1，对应途中的红色路径，但是1这个点已经被遍历过了，所以就出现了一个环，1->a->b->n->c->1,按照上述思路，把这个环的边权异或值存入数组中，记录下来。

线性基中只有这一个值，最终结果为:

  也是1->n的一条路径，则这条路径上的边权异或值最大。相当于1-a->b->n走完之后再走一个环，等于n->c->1的边权值。

ac代码：

---

#include
using namespace std;
typedef long long ll;
const int maxn=5e4+10;
const int max_base=60;
struct node{
    ll to;
    ll value;
};
vector vertex[maxn];
ll xorsum[maxn],p[max_base+3];;//存1到该点的异或值，存线性基
ll n,m,x,y,val;
int vis[maxn]={0};
vector v,cycle;//存不为0的p[]，存环的异或值,
void dfs(ll now,ll xorval)
{
    vis[now]=1;
    xorsum[now]=xorval;//1->now不包含回路的异或值
    for(int i=0;i=0;j--)
        {
            if(cycle[i]>>j&1)
            {
                if(p[j])
                    cycle[i]^=p[j];
                else
                {
                    p[j]=cycle[i];
                    break;
                }
            }
        }
    }
    for(int i=max_base;i>=0;i--)
        if(p[i])
            v.push_back(p[i]);
}
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    scanf("%lld %lld",&n,&m);
    for(int i=0;in某条路径上边权的异或和
    for(int i=0;i