基于Python的数据结构(一)-- 排序算法
基于Python的数据结构
- 内容说明
- 什么是排序
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序(递减递增排序)
- 归并排序
- 快速排序
- 总结
内容说明
最近在面试,在面试过程中面试官经常会要求手写代码。其中大都是数据结构及其查找和排序的基本算法,所以基于python-data-structure-cn这本书的内容对数据结构进行个人理解及代码实现。由于个人的阅读习惯原因,分享内容的顺序可能与书中不一致。原书地址如下,有学习的小伙伴可以直接在线阅读和练习。
https://facert.gitbooks.io/python-data-structure-cn
什么是排序
排序是以某种顺序从集合中放置元素的过程。对大量项进行排序可能需要大量的计算资源。排序算法的效率与正在处理的项的数量有关。对于小集合,复杂的排序方法可能更麻烦,开销太高。另一方面,对于更大的集合,我们希望利用尽可能多的改进。
分析排序算法时,可用于分析排序过程的操作:
- 比较的总数 ,在进行排序的过程中,必须对两个值进行比较,这就需要一些系统的方法来比较值。比较的总数将是测量排序过程的最常见方法;
- 交换的总数,当值相对于彼此不在正确的位置时,可能需要交换它们。这种交换是一种昂贵的操作,并且交换的总数对于评估算法的整体效率也将是很重要的。
下面就向大家介绍常见的几种算法。
冒泡排序
算法原理:逐次遍历列表元素,两两比较,每次将较大的值放在右边,每次遍历都会把最大值放在最右侧,即每次遍历的次数都减一. n,n-1,n-2…, 算法复杂度为O(n2)。

优缺点:冒泡排序通常被认为是最低效的排序方法,因为它必须在最终位置被知道之前交换项。但冒泡排序具有识别排序列表和及时停止的优点。
变种:短冒泡排序–判断是否已经完全排序,如果已经完全排序则停止遍历。
代码实现:
# 冒泡排序
def bubble_sort(alist):
for i in range(len(alist)-1,0,-1):
for j in range(i):
if alist[j]>alist[j+1]:
alist[j], alist[j+1] = alist[j+1],alist[j]
return alist
# 短冒泡排序
def Shortbubblesort(alist):
ex=True
l=len(alist)-1
while l>0 and ex:
ex=False
for i in range(l):
if alist[i]>alist[i+1]:
ex=True
alist[i],alist[i+1]=alist[i+1],alist[i]
l = l-1
return alist
选择排序
算法原理:对整个列表进行遍历,每次遍历只做一次交换,将最大值放到最右边。遍历n-1次排序n个项。时间复杂度O(n2)。
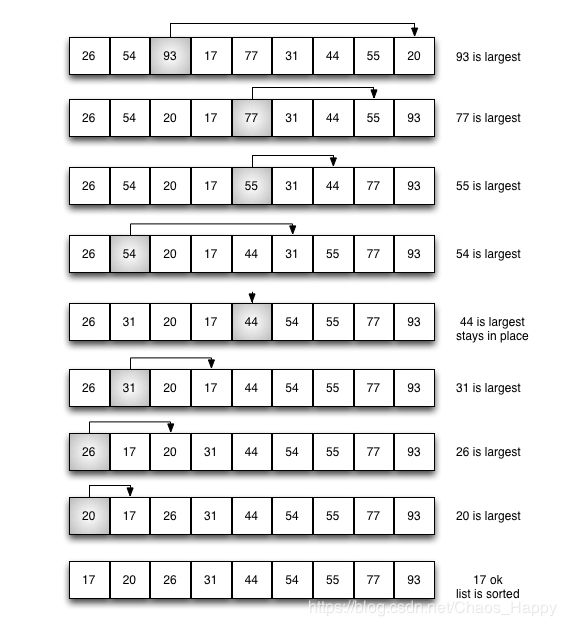
优缺点:与冒泡排序有相同的复杂度O(n2),然而交换数量的减少,选择排序通常在基准研究中执行的更快。
代码实现:
# 选择排序
def selectionsort(alist):
for i in range(len(alist)-1,0,-1):
lmax=i
for j in range(i):
if alist[j] > alist[lmax]:
lmax=j
alist[lmax],alist[i] = alist[i],alist[lmax]
return alist
c=[2,4,3,5,1,8]
selectionsort(c)
print(c)
插入排序
算法原理: 每次遍历都是通过维护列表的子列表的排序,对新加入的元素进行插入(移位),时间复杂度也是O(n2)。
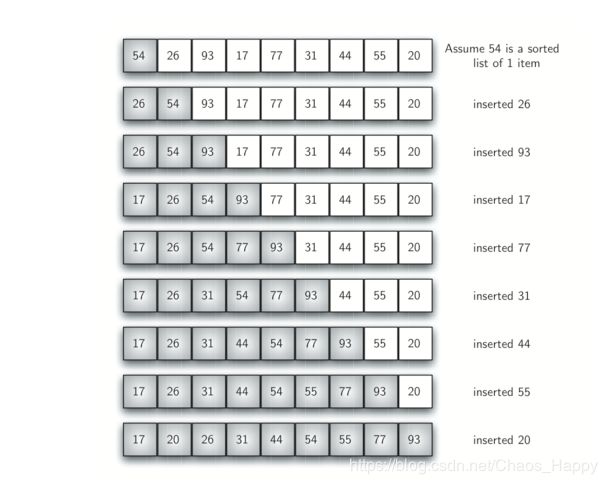
优缺点:存在n-1个遍历以对n个元素排序。从位置 1 开始迭代并移动位置到 n-1,因为这些是需要插回到排序子列表中的项。第 8 行执行移位操作,将值向上移动到列表中的一个位置,在其后插入。请记住,这不是像以前的算法中的完全交换。关于移位和交换的一个注意事项也很重要。通常,移位操作只需要交换大约三分之一的处理工作,因为仅执行一次分配.在基准研究中,插入排序有非常好的性能。
代码实现:
# 插入排序
def insertionsort(alist):
for i in range(1,len(alist)-1):
curvalue=alist[i]
index=i
while index>0 and alist[index-1]>curvalue:
alist[index]=alist[index-1]
index=index-1
alist[index]=curvalue
return alist
希尔排序(递减递增排序)
算法原理:将一个列表拆分为多个较小列表来改进插入排序,每个子列表使用插入排序进行排序。选择这些子列表的方是希尔排序的关键。不是将列表拆分为连续项的子列表,而是使用增量i(或者gap),通过选择i个项的所有项来创建子列表。最后再使用增量为1的插入排序:即标准插入排序。在通过执行之前的子列表排序后,我们减少了将列表置于其最终顺序所需的移位操作的总数。

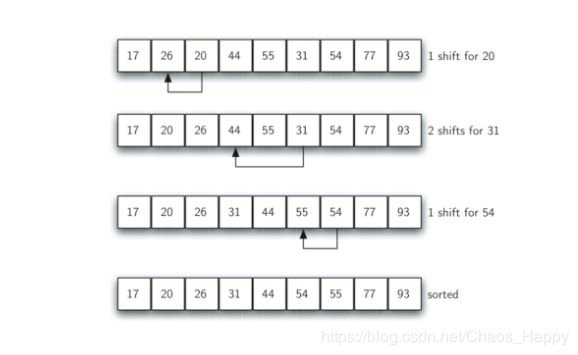
优缺点:希尔排序在每一次的遍历后都会产生比前一个更有序的列表,这使得最后一次的完整插入排序不需要进行更多的移位。它的时间复杂度落于O(n)与O(n2)之间的某处,比直接插入排序要快。
代码实现:
# 希尔排序
def gapInsertionSort(alist,start,gap): # 对子列表进行插入排序
for i in range(start+gap,len(alist),gap):
curvalue=alist[i]
index = i
while index >= gap and curvalue < alist[index-gap]:
alist[index] = alist[index-gap]
index = index-gap
alist[index]=curvalue
def ShellSort(alist): # 调用子列表插入排序函数,对增量进行逐次变化,以n/2为起始,最终1为止
gap=len(alist)//2
while gap > 0 :
for start in range(gap):
gapInsertionSort(alist,start,gap)
print('gap:',gap,'result:',alist)
gap = gap//2
归并排序
算法原理:归并排序的原理是分而治之,将列表依次从中间切割,直到切割到单一元素,之后再根据切割的顺序依次进行排序合并,最终达到排序的结果。其中实现的思想是通过递归进行分割和合并子列表。
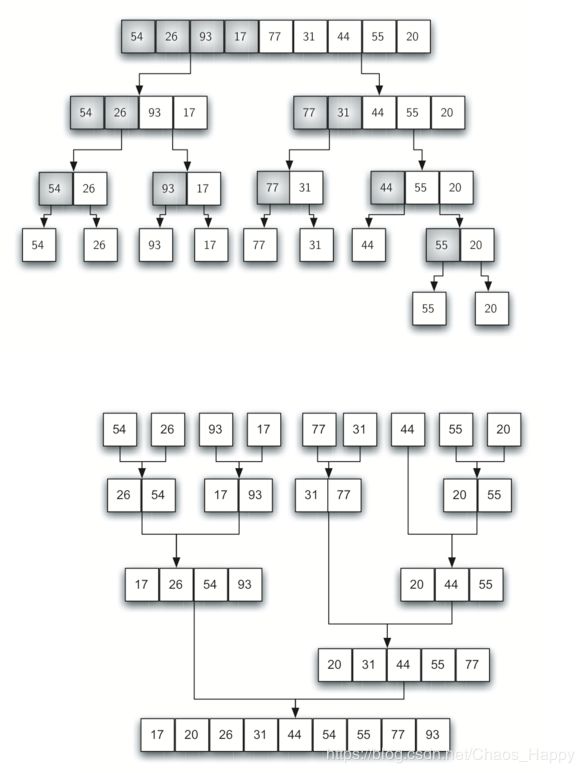
优缺点:通过两个不同的实现过程来分析。首先是将列表分为两半。将列表分为一般需要logn次,其中n是列表的长度。第二个过程是合并。列表中的每个项最终被处理并放置在排列的列表上。因此,大小为n的列表的合并操作需要n个操作。则归并排序的时间复杂度为O(nlogn)。但由于归并算法需要额外的空间来保存两个半部分,所以如果列表很大的时候会产生影响。
代码实现:
def mergesort(alist):
print("splitting:",alist)
if len(alist)>1:
mid = len(alist)//2
lefthalf=alist[:mid]
righthalf=alist[mid:]
mergesort(lefthalf)
mergesort(righthalf)
i=0
j=0
k=0
while i < len(lefthalf) and j < len(righthalf):
if lefthalf[i] > righthalf[j]:
alist[k]=righthalf[j]
j=j+1
else:
alist[k]=lefthalf[i]
i=i+1
k=k+1
while i < len(lefthalf):
alist[k]=lefthalf[i]
i=i+1
k=k+1
while j < len(righthalf):
alist[k]=righthalf[j]
j=j+1
k=k+1
print("Merging:",alist)
快速排序
算法原理:快速排序的原理也是分而治之,但不需要额外的空间。在快速排序中增加了一个新的角色–枢轴值(pivot)。枢轴值从英文释义上即中心,其作用是拆分列表,即列表进行拆分时的拆分点。实现过程为:首先在列表中选择一个元素为枢轴点,按照枢轴值左侧的值小于枢轴点,右侧的值大于枢轴点的逻辑从列表两端进行遍历并移位,当左侧标记点的位置大于右侧标记点的位置时,右侧标记点的位置即为拆分位置,将拆分位置的元素与枢轴值进行交换后,即得到第一次排序。后续经过递归操作,对拆分点左右两侧的子列表分别进行拆分排序,最终完成整体排序。

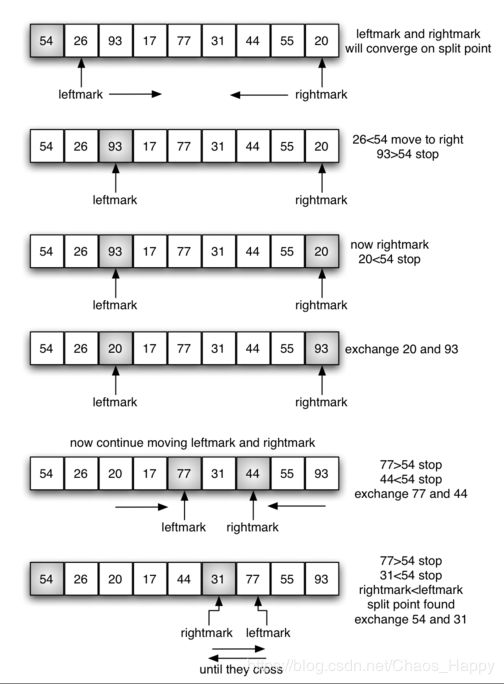
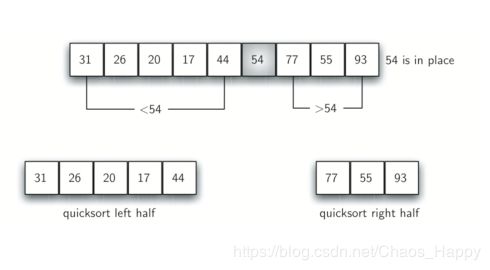
优缺点:快速排序在进行拆分的时候不会占用额外空间,如果分裂点在列表中间,则时间为O(nlogn),但是当分裂点不在列表中间,则时间为O(n2),所以选择枢轴值是方法很重要的。常用的方法是中值三:考虑第一个元素,中间元素和最后一个元素。然后选择中间值为枢轴值。这样将选出更好的中间值,当原列表部分有序时将特别有用。
代码实现:
def quickSort(alist):
quickSortHelper(alist,0,len(alist)-1)
def quickSortHelper(alist,first,last):
if first= pivotvalue and rightmark >= leftmark:
rightmark = rightmark -1
if rightmark < leftmark:
done = True
else:
temp = alist[leftmark]
alist[leftmark] = alist[rightmark]
alist[rightmark] = temp
temp = alist[first]
alist[first] = alist[rightmark]
alist[rightmark] = temp
return rightmark
总结
冒泡排序,选择排序和插入排序是 O(n2)算法。
希尔排序通过排序增量子列表来改进插入排序。它落在 O(n) 和 O(n2) 之间。
归并排序是 O(nlogn),但是合并过程需要额外的空间。
快速排序是 O(nlogn),但如果分割点不在列表中间附近,可能会降级到O(n2) 。它不需要额外的空间。