原文:https://subetter.com/algorith...
本篇针对面试中常见的二叉树操作作个总结:
(1)前序遍历,中序遍历,后序遍历;
(2)层次遍历;
(3)求树的节点数;
(4)求树的叶子数;
(5)求树的深度;
(6)求二叉树第k层的节点个数;
(7)判断两棵二叉树是否结构相同;
(8)求二叉树的镜像;
(9)求两个节点的最低公共祖先节点;
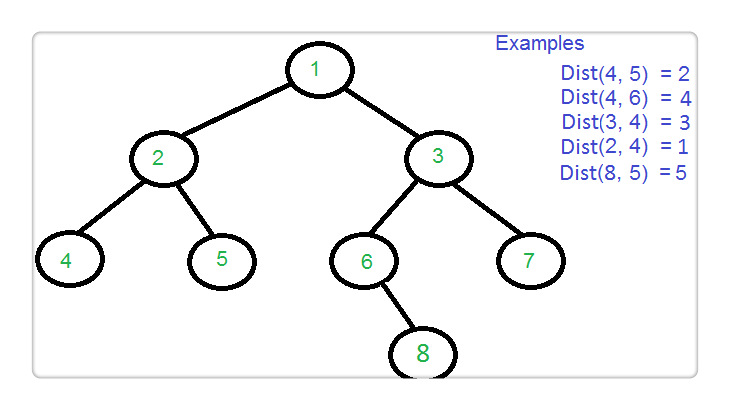
(10)求任意两节点距离;
(11)找出二叉树中某个节点的所有祖先节点;
(12)不使用递归和栈遍历二叉树;
(13)二叉树前序中序推后序;
(14)判断二叉树是不是完全二叉树;
(15)判断是否是二叉查找树的后序遍历结果;
(16)给定一个二叉查找树中的节点,找出在中序遍历下它的后继和前驱;
(17)二分查找树转化为排序的循环双链表;
(18)有序链表转化为平衡的二分查找树。
1-4
参见二叉树基础。
5 求树的深度
int GetDepth(Node * node)
{
if (node == nullptr)
return 0;
int left_depth = GetDepth(node->left) + 1;
int right_depth = GetDepth(node->right) + 1;
return left_depth > right_depth ? left_depth : right_depth;
}6 求二叉树第k层的节点个数
int GetKLevel(Node * node, int k)
{
if (node == nullptr || k < 1)
return 0;
if (k == 1)
return 1;
return GetKLevel(node->left, k - 1) + GetKLevel(node->right, k - 1);
}7 判断两棵二叉树是否结构相同
不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
bool StructureCmp(Node * node1, Node * node2)
{
if (node1 == nullptr && node2 == nullptr)
return true;
else if (node1 == nullptr || node2 == nullptr)
return false;
bool result_left = StructureCmp(node1->left, node2->left);
bool result_right = StructureCmp(node1->right, node2->right);
return result_left && result_right;
}8 求二叉树的镜像
对于每个节点,我们交换它的左右孩子即可。
void Mirror(Node * node)
{
if (node == nullptr)
return;
Node * temp = node->left;
node->left = node->right;
node->right = temp;
Mirror(node->left);
Mirror(node->right);
}9 求两个节点的最低公共祖先节点
最低公共祖先,即LCA(Lowest Common Ancestor),见下图: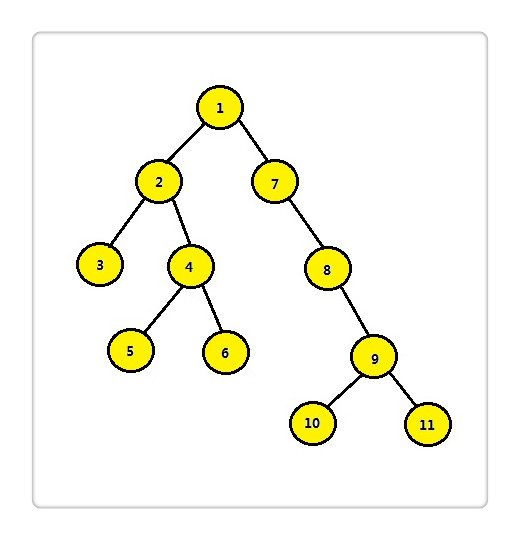
结点3和结点4的最近公共祖先是结点2,即LCA(3 ,4)=2。在此,需要注意到当两个结点在同一棵子树上的情况,如结点3和结点2的最近公共祖先为2,即 LCA(3,2)=2。同理LCA(5,6)=4,LCA(6,10)=1。
Node * FindLCA(Node * node, Node * target1, Node * target2)
{
if (node == nullptr)
return nullptr;
if (node == target1 || node == target2)
return node;
Node * left = FindLCA(node->left, target1, target2);
Node * right = FindLCA(node->right, target1, target2);
if (left && right) //分别在左右子树
return node;
return left ? left : right; //都在左子树或右子树
}10 求任意两节点距离
首先找到两个节点的LCA,然后分别计算LCA与它们的距离,最后相加即可。
int FindLevel(Node * node, Node * target)
{
if (node == nullptr)
return -1;
if (node == target)
return 0;
int level = FindLevel(node->left, target); //先在左子树找
if (level == -1)
level = FindLevel(node->right, target); //如果左子树没找到,在右子树找
if (level != -1) //找到了,回溯
return level + 1;
return -1; //如果左右子树都没找到
}
int DistanceNodes(Node * node, Node * target1, Node * target2)
{
Node * lca = FindLCA(node, target1, target2); //找到最低公共祖先节点
int level1 = FindLevel(lca, target1);
int level2 = FindLevel(lca, target2);
return level1 + level2;
}11 找出二叉树中某个节点的所有祖先节点
如果给定节点5,则其所有祖先节点为4,2,1。
bool FindAllAncestors(Node * node, Node * target)
{
if (node == nullptr)
return false;
if (node == target)
return true;
if (FindAllAncestors(node->left, target) || FindAllAncestors(node->right, target)) //找到了
{
cout << node->data << " ";
return true; //回溯
}
return false; //如果左右子树都没找到
}12 不使用递归和栈遍历二叉树
1968年,高德纳(Donald Knuth)提出一个问题:是否存在一个算法,它不使用栈也不破坏二叉树结构,但是可以完成对二叉树的遍历?随后1979年,James H. Morris提出了二叉树线索化,解决了这个问题。(根据这个概念我们又提出了一个新的数据结构,即线索二叉树,因线索二叉树不是本文要介绍的内容,所以有兴趣的朋友请移步线索二叉树。)
前序,中序,后序遍历,不管是递归版本还是非递归版本,都用到了一个数据结构--栈,为何要用栈?那是因为其它的方式没法记录当前节点的parent,而如果在每个节点的结构里面加个parent分量显然是不现实的,而线索化正好解决了这个问题,其含义就是利用节点的右孩子空指针,指向该节点在中序序列中的后继。下面具体来看看如何使用线索化来完成对二叉树的遍历。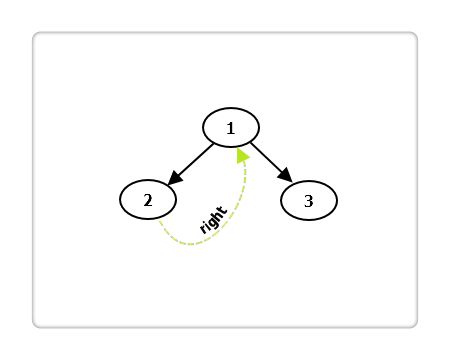
先看前序遍历,步骤如下:
(1)如果当前节点的左孩子为空,则输出当前节点并将其右孩子作为当前节点;
(2)如果当前节点的左孩子不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点;
(2.1)如果前驱节点的右孩子为空,将它的右孩子设置为当前节点,输出当前节点并把当前节点更新为当前节点的左孩子;
(2.2)如果前驱节点的右孩子为当前节点,将它的右孩子重新设为空,当前节点更新为当前节点的右孩子;
(3)重复以上(1)和(2),直到当前节点为空。
/* 前序遍历 */
void PreOrderMorris(Node * root)
{
Node * cur = root;
Node * pre = nullptr;
while (cur)
{
if (cur->left == nullptr) //(1)
{
cout << cur->data << " ";
cur = cur->right;
}
else
{
pre = cur->left;
while (pre->right && pre->right != cur) //(2),找到cur的前驱节点
pre = pre->right;
if (pre->right == nullptr) //(2.1),cur未被访问,将cur节点作为其前驱节点的右孩子
{
cout << cur->data << " ";
pre->right = cur;
cur = cur->left;
}
else //(2.2),cur已被访问,恢复树的原有结构,更改right指针
{
pre->right = nullptr;
cur = cur->right;
}
}
}
} 再来看中序遍历,和前序遍历相比只改动一句代码,步骤如下:
(1)如果当前节点的左孩子为空,则输出当前节点并将其右孩子作为当前节点;
(2)如果当前节点的左孩子不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点;
(2.1)如果前驱节点的右孩子为空,将它的右孩子设置为当前节点,当前节点更新为当前节点的左孩子;
(2.2)如果前驱节点的右孩子为当前节点,将它的右孩子重新设为空,输出当前节点,当前节点更新为当前节点的右孩子;
(3)重复以上(1)和(2),直到当前节点为空。
/* 中序遍历 */
void InOrderMorris(Node * root)
{
Node * cur = root;
Node * pre = nullptr;
while (cur)
{
if (cur->left == nullptr) //(1)
{
cout << cur->data << " ";
cur = cur->right;
}
else
{
pre = cur->left;
while (pre->right && pre->right != cur) //(2),找到cur的前驱节点
pre = pre->right;
if (pre->right == nullptr) //(2.1),cur未被访问,将cur节点作为其前驱节点的右孩子
{
pre->right = cur;
cur = cur->left;
}
else //(2.2),cur已被访问,恢复树的原有结构,更改right指针
{
cout << cur->data << " ";
pre->right = nullptr;
cur = cur->right;
}
}
}
} 最后看下后序遍历,后续遍历有点复杂,需要建立一个虚假根节点dummy,令其左孩子是root。并且还需要一个子过程,就是倒序输出某两个节点之间路径上的各个节点。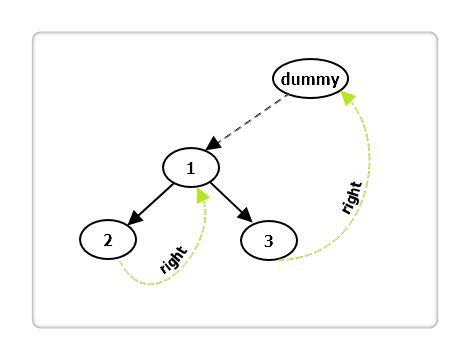
步骤如下:
(1)如果当前节点的左孩子为空,则将其右孩子作为当前节点。
(2)如果当前节点的左孩子不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
(2.1)如果前驱节点的右孩子为空,将它的右孩子设置为当前节点,当前节点更新为当前节点的左孩子;
(2.2)如果前驱节点的右孩子为当前节点,将它的右孩子重新设为空,倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点,当前节点更新为当前节点的右孩子;
(3)重复以上(1)和(2),直到当前节点为空。
struct Node
{
int data;
Node * left;
Node * right;
Node(int data_, Node * left_, Node * right_)
{
data = data_;
left = left_;
right = right_;
}
};
void ReversePrint(Node * from, Node * to)
{
if (from == to)
{
cout << from->data << " ";
return;
}
ReversePrint(from->right, to);
cout << from->data << " ";
}
void PostOrderMorris(Node * root)
{
Node * dummy = new Node(-1, root, nullptr); //一个虚假根节点
Node * cur = dummy;
Node * pre = nullptr;
while (cur)
{
if (cur->left == nullptr) //(1)
cur = cur->right;
else
{
pre = cur->left;
while (pre->right && pre->right != cur) //(2),找到cur的前驱节点
pre = pre->right;
if (pre->right == nullptr) //(2.1),cur未被访问,将cur节点作为其前驱节点的右孩子
{
pre->right = cur;
cur = cur->left;
}
else //(2.2),cur已被访问,恢复树的原有结构,更改right指针
{
pre->right = nullptr;
ReversePrint(cur->left, pre);
cur = cur->right;
}
}
}
}dummy用的非常巧妙,建议读者配合上面的图模拟下算法流程。
13 二叉树前序中序推后序
前序:[1 2 4 7 3 5 8 9 6]
中序:[4 7 2 1 8 5 9 3 6]
后序:[7 4 2 8 9 5 6 3 1]
以上式为例,步骤如下:
第一步:根据前序可知根节点为1;
第二步:根据中序可知4 7 2为根节点1的左子树和8 5 9 3 6为根节点1的右子树;
第三步:递归实现,把4 7 2当做新的一棵树和8 5 9 3 6也当做新的一棵树;
第四步:在递归的过程中输出后序。
/* 前序遍历和中序遍历结果以长度为n的数组存储,pos1为前序数组下标,pos2为后序下标 */
int pre_order_arry[n];
int in_order_arry[n];
void PrintPostOrder(int pos1, int pos2, int n)
{
if (n == 1)
{
cout << pre_order_arry[pos1];
return;
}
if (n == 0)
return;
int i = 0;
for (; pre_order_arry[pos1] != in_order_arry[pos2 + i]; i++);
PrintPostOrder(pos1 + 1, pos2, i);
PrintPostOrder(pos1 + i + 1, pos2 + i + 1, n - i - 1);
cout << pre_order_arry[pos1];
}当然我们也可以根据前序和中序构造出二叉树,进而求出后序。
/* 该函数返回二叉树的根节点 */
Node * Create(int pos1, int pos2, int n)
{
Node * p = nullptr;
for (int i = 0; i < n; i++)
{
if (pre_order_arry[pos1] == in_order_arry[pos2])
{
p = new Node(pre_order_arry[pos1]);
p->left = Create(pos1 + 1, pos2, i);
p->right = Create(pos1 + i + 1, pos2 + i + 1, n - i - 1);
return p;
}
}
return p;
}14 判断二叉树是不是完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树(Complete Binary Tree)。如下图: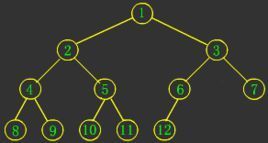
首先若一个节点只有右孩子,肯定不是完全二叉树;其次若只有左孩子或没有孩子,那么对于一个高度为h的完全二叉树,当前节点的高度肯定是h-1,也就是高度h的所有节点都没有孩子,否则不是完全二叉树,因此设置flag标记当前节点是不是到了h-1高度。
bool IsCBT(Node * node)
{
bool flag = false;
queue Q;
Q.push(node);
while (!Q.empty())
{
Node * p = Q.front();
Q.pop();
if (flag)
{
if (p->left || p->right)
return false;
}
else
{
if (p->left && p->right)
{
Q.push(p->left);
Q.push(p->right);
}
else if (p->right) //只有右节点
return false;
else if (p->left) //只有左节点
{
Q.push(p->left);
flag = true;
}
else //没有节点
flag = true;
}
}
return true;
} 15 判断是否是二叉查找树的后序遍历结果
在后续遍历得到的序列中,最后一个元素为树的根结点。从头开始扫描这个序列,比根结点小的元素都应该位于序列的左半部分;从第一个大于跟结点开始到跟结点前面的一个元素为止,所有元素都应该大于跟结点,因为这部分元素对应的是树的右子树。根据这样的划分,把序列划分为左右两部分,我们递归地确认序列的左、右两部分是不是都是二元查找树。
int array[n]; //长度为n的序列,begin和end遵循的是左闭右闭原则
bool IsSequenceOfBST(int begin, int end)
{
if (end - begin <= 0)
return true;
int root_data = array[end]; //数组尾元素为根节点
int i = begin;
for (; array[i] < root_data; i++); //取得左子树
int j = i;
for (; j < end; j++)
if (array[j] < root_data) //此时右子树应该都大于根节点;若存在小于的,
return false;
return IsSequenceOfBST(begin, i - 1) && IsSequenceOfBST(i, end - 1); //左右子树是否都满足
}16 给定一个二叉查找树中的节点,找出在中序遍历下它的后继和前驱
一棵二叉查找树的中序遍历序列,正好是升序序列。
如果节点中有指向父亲节点的指针(假如根节点的父节点为nullptr),则:
(1)如果当前节点有右孩子,则后继节点为这个右孩子的最左孩子;
(2)如果当前节点没有右孩子;
(2.1)当前节点为根节点,返回nullptr;
(2.2)当前节点只是个普通节点,也就是存在父节点;
(2.2.1)当前节点是父亲节点的左孩子,则父亲节点就是后继节点;
(2.2.2)当前节点是父亲节点的右孩子,沿着父亲节点往上走,直到n-1代祖先是n代祖先的左孩子,则后继为n代祖先)或遍历到根节点也没找到符合的,则当前节点就是中序遍历的最后一个节点,返回nullptr。
/* 求后继节点 */
Node * Increment(Node * node)
{
if (node->right) //(1)
{
node = node->right;
while (node->left)
node = node->left;
return node;
}
else //(2)
{
if (node->parent == nullptr) //(2.1)
return nullptr;
Node * p = node->parent; //(2.2)
if (p->left == node) //(2.2.1)
return p;
else //(2.2.2)
{
while (p->right == node)
{
node = p;
p = p->parent;
if (p == nullptr)
return nullptr;
}
return p;
}
}
}仔细观察上述代码,总觉得有点啰嗦。比如,过多的return,(2)的层次太多。综合考虑所有情况,改进代码如下:
Node * Increment(Node * node)
{
if (node->right)
{
node = node->right;
while (node->left)
node = node->left;
}
else
{
Node * p = node->parent;
while (p && p->right == node)
{
node = p;
p = p->parent;
}
node = p;
}
return node;
} 上述的代码是基于节点有parent指针的,若题意要求没有parent呢?网上也有人给出了答案,个人觉得没有什么价值,有兴趣的朋友可以到这里查看。
而求前驱节点的话,只需把上述代码的left与right互调即可,很简单。
17 二分查找树转化为排序的循环双链表
二分查找树的中序遍历即为升序排列,问题就在于如何在遍历的时候更改指针的指向。一种简单的方法时,遍历二分查找树,将遍历的结果放在一个数组中,之后再把该数组转化为双链表。如果题目要求只能使用$O(1)$内存,则只能在遍历的同时构建双链表,即进行指针的替换。
我们需要用递归的方法来解决,假定每个递归调用都会返回构建好的双链表,可把问题分解为左右两个子树。由于左右子树都已经是有序的,当前节点作为中间的一个节点,把左右子树得到的链表连接起来即可。
/* 合并两个a,b两个循环双向链表 */
Node * Append(Node * a, Node * b)
{
if (a == nullptr) return b;
if (b == nullptr) return a;
//分别得到两个链表的最后一个元素
Node * a_last = a->left;
Node * b_last = b->left;
//将两个链表头尾相连
a_last->right = b;
b->left = a_last;
a->left = b_last;
b_last->right = a;
return a;
}
/* 递归的解决二叉树转换为双链表 */
Node * TreeToList(Node * node)
{
if (node == nullptr) return nullptr;
//递归解决子树
Node * left_list = TreeToList(node->left);
Node * right_list = TreeToList(node->right);
//把根节点转换为一个节点的双链表。方便后面的链表合并
node->left = node;
node->right = node;
//合并之后即为升序排列
left_list = Append(left_list, node);
left_list = Append(left_list, right_list);
return left_list;
}18 有序链表转化为平衡的二分查找树(Binary Search Tree)
我们可以采用自顶向下的方法。先找到中间节点作为根节点,然后递归左右两部分。所有我们需要先找到中间节点,对于单链表来说,必须要遍历一边,可以使用快慢指针加快查找速度。
struct TreeNode
{
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int data_) { data = data_; left = right = nullptr; }
};
struct ListNode
{
int data;
ListNode* next;
ListNode(int data_) { data = data_; next = nullptr; }
};
TreeNode * SortedListToBST(ListNode * list_node)
{
if (!list_node) return nullptr;
if (!list_node->next) return (new TreeNode(list_node->data));
//用快慢指针找到中间节点
ListNode * pre_slow = nullptr; //记录慢指针的前一个节点
ListNode * slow = list_node; //慢指针
ListNode * fast = list_node; //快指针
while (fast && fast->next)
{
pre_slow = slow;
slow = slow->next;
fast = fast->next->next;
}
TreeNode * mid = new TreeNode(slow->data);
//分别递归左右两部分
if (pre_slow)
{
pre_slow->next = nullptr;
mid->left = SortedListToBST(list_node);
}
mid->right = SortedListToBST(slow->next);
return mid;
} 由$f(n)=2f(\frac n2)+\frac n2$得,所以上述算法的时间复杂度为$O(nlogn)$。
不妨换个思路,采用自底向上的方法:
TreeNode * SortedListToBST(ListNode *& list, int start, int end)
{
if (start > end) return nullptr;
int mid = start + (end - start) / 2;
TreeNode * left_child = SortedListToBST(list, start, mid - 1); //注意此处传入的是引用
TreeNode * parent = new TreeNode(list->data);
parent->left = left_child;
list = list->next;
parent->right = SortedListToBST(list, mid + 1, end);
return parent;
}
TreeNode * sortedListToBST(ListNode * node)
{
int n = 0;
ListNode * p = node;
while (p)
{
n++;
p = p->next;
}
return SortedListToBST(node, 0, n - 1);
}如此,时间复杂度降为$O(n)$。