【论文笔记】VGG
介绍
在这篇文章中,作者对传统的卷积网络在“深度”方面进行了拓展。
卷积网络配置
结构
训练阶段,我们的卷积网络的输入是固定大小为224 x 224的RGB图像。
配置
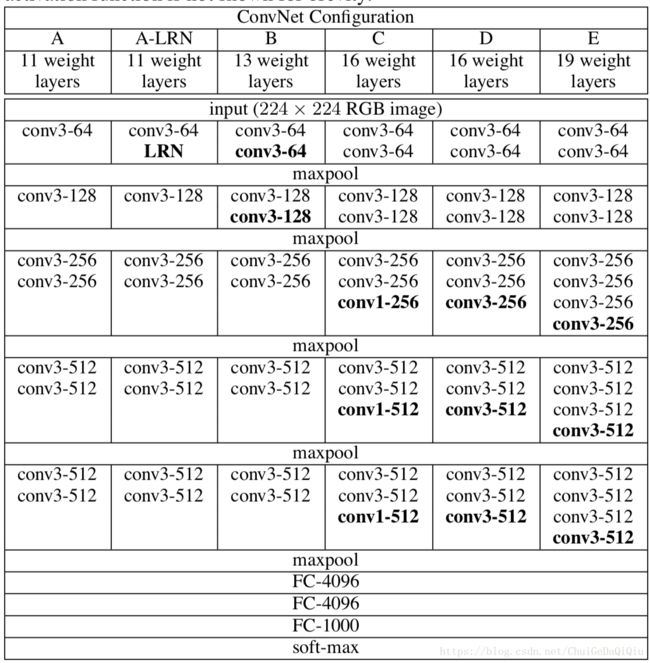
表1是本论文中所评测的卷积网络的配置,每一列表示一种网络结构。所列的这些网络唯一的不同在于他们的深度。卷积层的宽度都相当地窄,从第一层的64开始,每过一个最大池化层(max-polling layer)翻一倍,直到512。
表2是每种网络结构的参数数量。
讨论
我们的卷积网络配置不同于之前在ILSVRC-2012和ILSVRC-2013表现突出的竞赛方案。在第一个卷积层没有使用相对大的感受野,而是在整个网络中使用了3 x 3的感受野。我们使用一堆3 x 3的卷积层取代一个单独的7 x 7的卷积层,这有什么好处呢?首先,我们引入了3个非线性修正层而不是1个。其次,减少了参数的数量。
1 x 1卷积层的引入在不影响卷积层感受野的情形下增加了决策函数的非线性特性。
表1:卷积网络配置
表2:参数数量
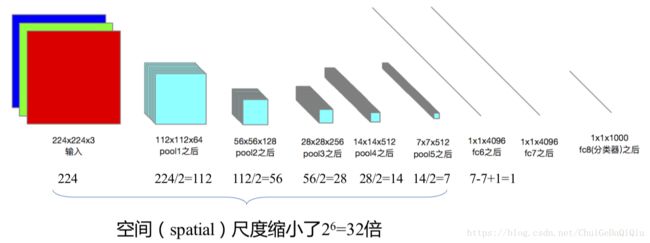
表3:网络中特征图尺寸和深度的变化
这里以C网络(VGG-16)为例,并结合tf-slim代码对网络进行补充说明。
def vgg_16(inputs,
num_classes=1000,
is_training=True,
dropout_keep_prob=0.5,
spatial_squeeze=True,
scope='vgg_16',
fc_conv_padding='VALID',
global_pool=False):
"""Oxford Net VGG 16-Layers version D
"""
with tf.variable_scope(scope, 'vgg_16', [inputs]) as sc:
end_points_collection = sc.original_name_scope + '_end_points'
# Collect outputs for conv2d, fully_connected and max_pool2d.
with slim.arg_scope([slim.conv2d, slim.fully_connected, slim.max_pool2d],
outputs_collections=end_points_collection):
#连续两个3x3的卷积操作,输出通道数皆为64,填充方式默认为'SAME'
net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 3, slim.conv2d, 256, [3, 3], scope='conv3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')
# Use conv2d instead of fully_connected layers.
# 对于固定输入大小为224x224的图像,经过上面5次2x2的最大池化后此时的特征图的尺寸已经正好变为7x7.
# 而深度为512.接下来的卷积操作卷积核大小正好为7x7,填充方式为'VALID',输出通道数为4096,所以这一
# 步卷积操作后的特征图为1x1x4096
net = slim.conv2d(net, 4096, [7, 7], padding=fc_conv_padding, scope='fc6')
net = slim.dropout(net, dropout_keep_prob, is_training=is_training, scope='dropout6')
net = slim.conv2d(net, 4096, [1, 1], scope='fc7')
# Convert end_points_collection into a end_point dict.
end_points = slim.utils.convert_collection_to_dict(end_points_collection)
if global_pool:
net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
end_points['global_pool'] = net
if num_classes:
net = slim.dropout(net, dropout_keep_prob, is_training=is_training, scope='dropout7')
net = slim.conv2d(net, num_classes, [1, 1],
activation_fn=None,
normalizer_fn=None,
scope='fc8')
if spatial_squeeze and num_classes is not None:
#这里相当对1x1x4096的特征图摊平为一维向量
net = tf.squeeze(net, [1, 2], name='fc8/squeezed')
end_points[sc.name + '/fc8'] = net
return net, end_points分类框架
训练
1、目标函数使用带动量的多项式回归成本函数;
2、优化算法为基于反向传播的批量梯度下降(mini-batch gradient descent);
3、每批数据量(batch size)大小为256,动量(momentum)为0.9;
4、使用权重衰减进行正则化(the L2 penalty multiplier set to 5*10^-4);
5、前两个全连接层使用dropout进行正则化,dropout比例为0.5;
6、初始学习率设置为0.01,当验证集中的准确率不再变化时再以10倍衰减。学习率总共衰减了3次,在370K次迭代(74个epochs)后停止训练。