关系模型之关系代数

关系代数的运算按运算符的不同可分为

• 传统的集合运算(并、差、交、笛卡尔积)
• 专门的关系运算(选择、投影、连接、除运算)

关系代数运算的约束

某些关系代数操作,如并、差、交等需满足 “并相容性”,下面是一个并相容性的示例:

STUDENT(SID `char(10)`,Sname `char(8)`,Age `char(3)`)
PROFESSOR(PID `char(10)`,Pname `char(8)`,Age `char(3)`)

两个关系是相容的.

并(Union)

定义:假设关系R和关系S是相容的,则关系R与关系S的并运算结果也是一个关系,记作:RUS,它由或者出现在关系R中,或者出现在S中的元组构成.

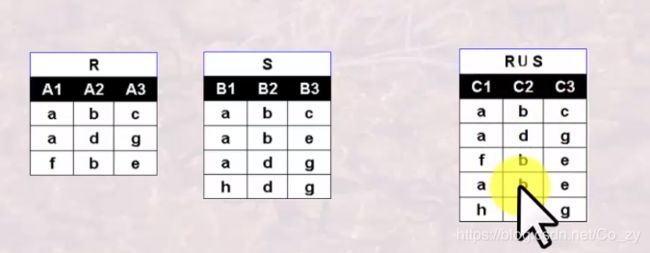
数学描述R∪S={ t | t∈R∨t∈S},其中t是元组
并运算是将两个关系的元组合并成一个关系,在合并时去掉重复的元组

差(Difference)

定义:假设关系R和关系S是相容的,则关系R与关系S的并运算结果也是一个关系,记作:R-S,它由出现在关系R中但不出现在关系S中的元组构成.

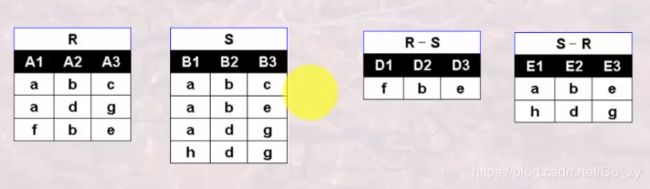
数学描述:R-S = { t | t∈R ∧ t∉S} (可以把t看做上图R-S中的f,b,e元组)

广义笛卡尔积(Cartesian Product)

RxS,它由关系R中的元组和关系S的元组进行所有可能的拼接(或串接)构成.(通过下图可以更好理解)

数学描述(复试笔试出现了这个,可惜当时没看懂)
这里的笛卡儿积严格地讲应该是广义的笛卡儿积（ extended cartesian product)，因为这里笛卡儿积的元素是元组。
两个分别为n目(就是列数,上图中n=2)和m目(上图中m=3)的关系R和S的笛卡儿积是一个(n+m)列的元组的集合。元组的前n列是关系R的一个元组，后m列是关系S的一个元组。若R有k1个元组，S有k2个元组，则关系R和关系S的笛卡儿积有k1 * k2个元组。
记作

选择(Select)

选择又称为限制(restriction),它是在关系R中选择满足给定条件的诸元组

数学描述

F表示选择条件,它是一个逻辑表达式,取真或假

投影(Project)

从关系R中选出属性包含在A中的 列 构成,投影运算可以对原关系的列在投影后重新排列.

其中A为R中的属性列

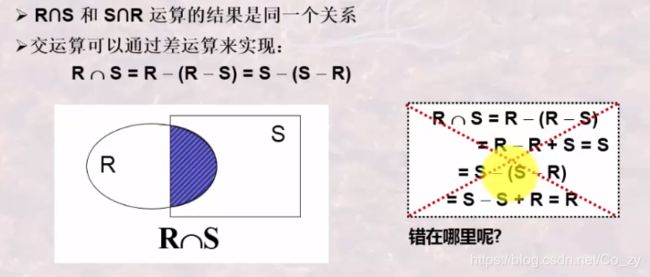
交(Intersection)

由同时出现在关系R和关系S中的元组构成

示例一

---

Θ-连接(Θ-Join,theta-Join)

投影与选择操作只是对单个关系(表)进行操作,而实际应用中往往涉及多个表之间的操作,这就需要Θ-连接操作. Θ是比较运算符(<,>,=)

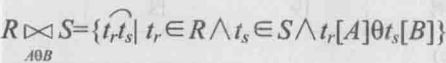
示例一(条件B<=H)

步骤:先计算笛卡尔积,如图中间所示,然后按照B<=H选择合适的行,最右边是连接操作,将符合B小于等于H的进行连接.

Θ-连接步骤

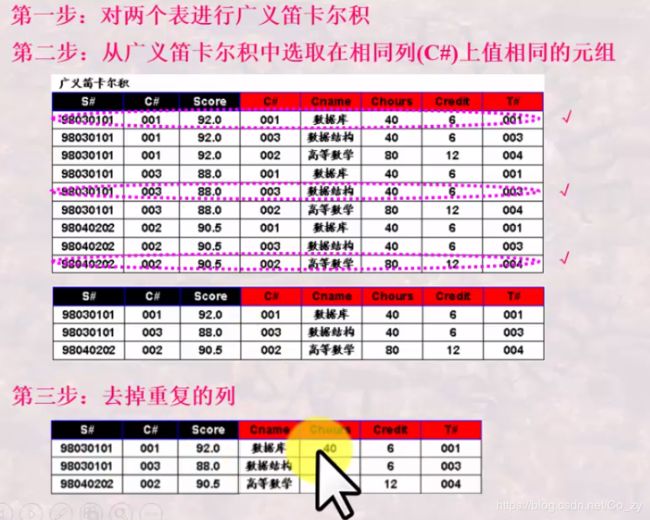
第一步:对两个表进行笛卡尔积
第二步:从广义笛卡尔积中选出符合条件的元组
第三步:进行投影操作,得到最终的结果

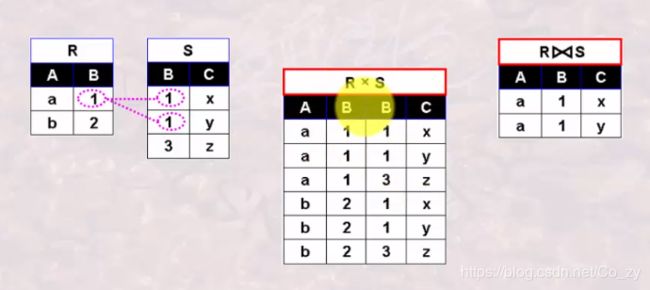
等值连接

由关系R和关系S的笛卡尔积中选取R中属性A与S中属性B上的值相等的元组所构成,当Θ-连接中运算符为=时,就是等值连接,等值连接是Θ-连接的一个特例.

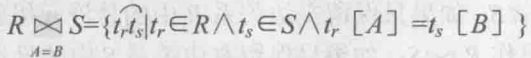
示例一

示例二

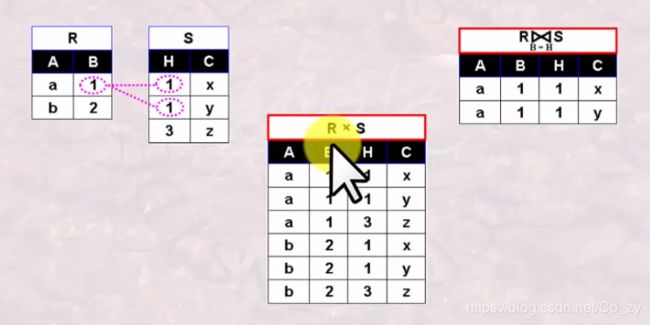
自然连接

由关系R和关系S的笛卡尔积中选取属性组B上值相等的元组所构成.

• 自然连接时一种特殊的等值连接
• 要求关系R和关系S必须有相同的属性组B(参考上面等值连接例子)
• R,S属性相同,值必须相等才能连接.

示例一

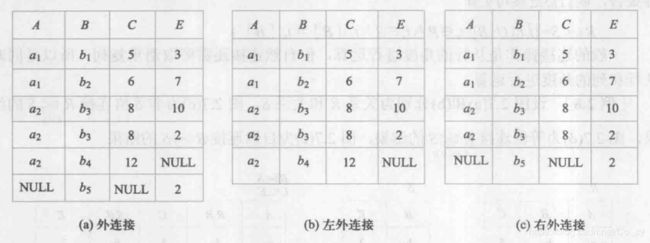
外链接

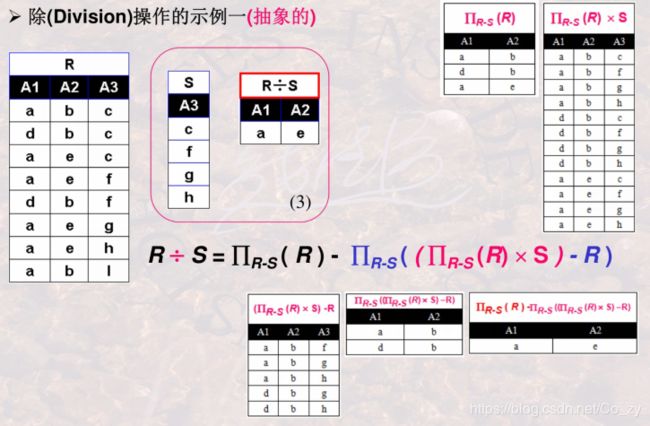
除运算

除法运算经常用于求解"查询…全部的/所有的…"的问题
R÷S结果的属性应该是R的属性去掉S在R中的属性
R÷S元组与S中每一个元组的组合必须在R中

示例一