数字图像处理 第一章
- 第一章:绪言
- 1.1 背景
- 1.2 什么是数字图像处理
- 1.3 MATLAB和图像处理工具箱基础
- 1.4 本书涵盖的图像处理范围
- 1.7 基本原理
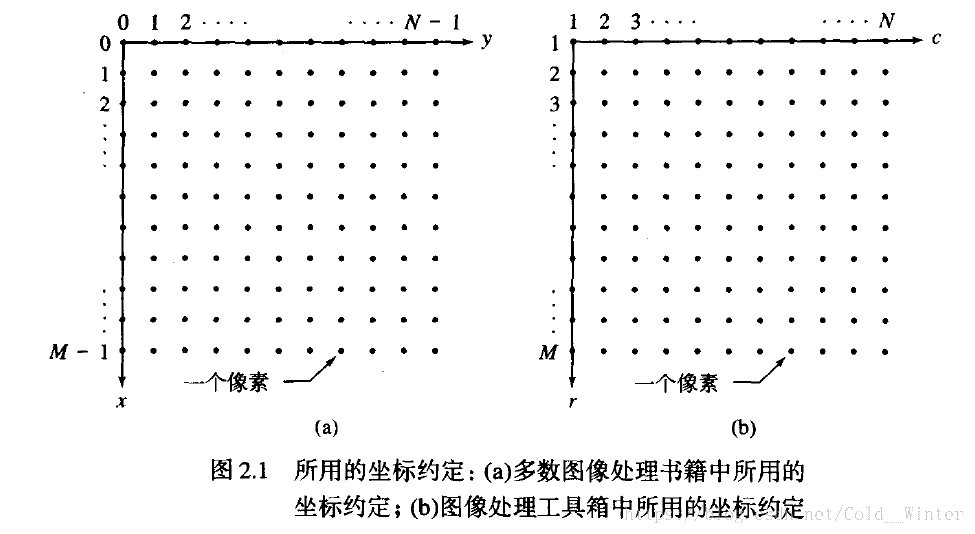
- 1.7.5 数字图像表示
- 1.7.6 图像的输入/输出和显示
- 1.7.7 类和图像类型
- 1.7.8 M函数编程
- M文件:
- 算术运算符
- 关系运算符
- 逻辑运算符
- 流控制
- 数组索引
- 函数句柄、单元数组和结构
- 代码优化
第一章:绪言
1.1 背景
本书的主要目的是将宽泛的理论概念和用现代图像处理软件工具实现这些概念所需知识结合在一起。以原理为基础,通过教材而非手册方式进行组织和介绍。
1.2 什么是数字图像处理
数字图像处理(Digital Image Processing)是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。数字图像处理的产生和迅速发展主要受三个因素的影响:一是计算机的发展;二是数学的发展(特别是离散数学理论的创立和完善);三是广泛的农牧业、林业、环境、军事、工业和医学等方面的应用需求的增长。
1.3 MATLAB和图像处理工具箱基础
MATLAB是一种用于技术计算的高性能语言。它将计算、可视化和变成集成于一种简易的环境中,以人们熟悉的数学表示法来表示问题及其解答。其典型应用包括如下部分:
- 数学和计算
- 算法开发
- 数据获取
- 建模,仿真和原型设计
- 数据分析,检测和可视化
- 科学和工程图形学
- 应用开发,包括图形用户界面构建
1.4 本书涵盖的图像处理范围
- 第二章:灰度变换与空间滤波
- 第三章:频率域滤波
- 第四章:图像复原与重建
- 第五章:彩色图像处理
- 第六章:图像压缩
- 第七章:图像分割
- 第八章:表示与描述
1.7 基本原理
1.7.5 数字图像表示
1.7.6 图像的输入/输出和显示
输入:
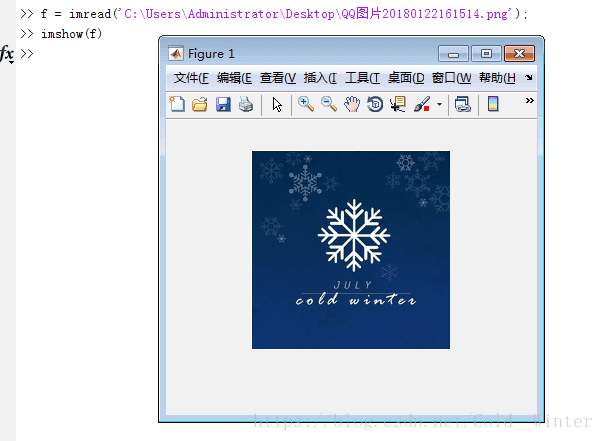
使用函数 imread 可将图像读入MATLAB环境中,基本用法是
imread('filename')此处,filename是一个含有图像文件全名的字符串(包括任何可用的扩展名)。例如:
>> f = imread('chestxray.jpg');函数imread支持多数流行的图像图形格式,包括JPEG和TIFF
输出:
使用函数 imshow 可将图像显示在MATLAB桌面上,该函数的基本语法为:
imshow(f)其中,f是一个图像数组。
例子:
>> f = imread('rose_512.tif');
>> imshow(f)如果随后使用imshow显示另一幅图像g,MATLAB会用新图像取代图形窗口中的图像。要保留第一幅图并输出第二幅图像,可按如下方式使用函数figure:
>> figure, imshow(g)图像被函数imwrite写入当前目录,具有如下基本用法:
imwrite(f,'filename')函数imwrite还可以有其他参数,取决于将被写的文件格式。更为通用的imwriteuifa是
imwrite(f, 'filename', 'quality', q)其中q是从0到100之间的一个整数(对于JPEG压缩,数字越小,劣化越高)。
1.7.7 类和图像类型
虽然我们使用整数坐标,但是在MATLAB中像素值(灰度)并没限制为整数。表列出了MATLAB和图像处理工具箱为描述像素值所支持的各种类。

工具箱支持4中图像类型:
- 灰度级图像
- 二值图像
- 索引图像
- RGB图像
关于二值图像:
使用函数logical可将数值数组转换为二值图像
B = logical(A)可以使用函数islogical来测试一个数组是否是logical类
iflogical(C)1.7.8 M函数编程
M文件:
M文件由文本编辑器创建,并以形式为filenamne.m的文件名保存。组成部分如下:
- 函数定义行
- H1行
- 帮助文本
- 函数体
- 注释
函数定义行具有如下形式:
function [outputs] = name(inputs)例如,一个计算两幅图像的和与积的函数一个有如下形式:
function [s,p] = sunprod(f,g)其中,f和g是输入图像,s是和图像,p是积图像。名词sumprod是任意选择的,但单词function总是出现在左侧。函数名不虚以字母开头,余下可以是字母数字和下划线的任意组合,不允许有空格。
函数可以在命令提示符处调用。例如,
>> [s,p] = sumprod(f,g);H1行是第一个文本行,它是函数定义行后面的单独的注释行。他们之间可以没有空行或前导空格,例子:
%SUMPROD Computes the sum and product of two images.当用户输入
>> help function_nameH1行是最先出现的文本。
帮助文本是紧跟在H1行后面的文本块,两者之间没有空行。
符号“%”后面的非H1行或帮助文本的所有行,都被认为是注释行,并且也不认识是帮助文本块的一部分。
M文件可以使用任何文本编辑器来创建和编辑,并且可以扩展名.m保存到指定的目录下。创建或编辑M文件的另一种方法是在提示符的后面使用edit函数。例如:
>> edit sumprod就会打开文件sumprod进行编辑,如果找不到,MATLAB就会创造文件。
算术运算符
MATLAB有两种不同类型的算术运算符。矩阵算术运算按线性代数的规则来定义,数组算术运算则逐个元素地执行,且可以使用多维数组。句点字符(.)用来区分数组运算与矩阵运算。

关系运算符
逻辑运算符
流控制
数组索引

使用转置运算符(.’),可将行向量转换为列向量(反之亦然):
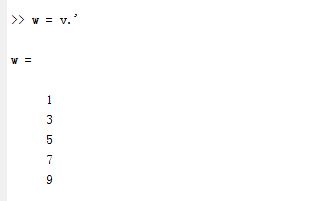
要访问元素块,可以用冒号,比如要访问v的前三个元素:
>> v(1:3)
ans =
1 3 5类似的,可以使用如下语句访问第三个到最后一个元素:
>> v(3:end)
ans =
5 7 9其中,end表示向量中的最后一个元素。
还可以用一个向量作为另一个向量的索引:
>> v([1 4 5])
ans =
1 7 9此外,索引不限于相邻的元素,例如:
>> v(1:2:end)
ans =
1 5 9其中,符号1:2:end表示从1开始,以2为加数相加,当计数到达最后一个元素时则停止
在MATLAB中,矩阵可以方便地表示为一系列行向量,这些行向量由方括号括器并由分号分隔。例如,键入
>> A = [1 2 3; 4 5 6; 7 8 9]
给出一个3×3矩阵
A =
1 2 3
4 5 6
7 8 9我们可以按处理向量的方式来选取矩阵中的元素,但需要两个索引:一个对应行,一个对应列。
也可以使用一个冒号作为索引来选择整行、整列或整个矩阵:
>> A(2,:)
ans =
4 5 6
>> sum(A(:))
ans =
45函数sum计算其参量的每一列的和,单冒号索引把A变换为列向量,并将结果传递给sum。
另一种相当有用的索引形式是逻辑索引。逻辑索引具有形式A(D),其中A是一个数组,D是与A相同大小的络技术组。表达式A(D)提取A中与D中的1值元素相对应的所有元素,比如:
>> D = logical([1 0 0; 0 0 1; 0 0 0])
D =
3×3 logical 数组
1 0 0
0 0 1
0 0 0
>> A(D)
ans =
1
6函数句柄、单元数组和结构
函数句柄是一种MATLAB数据类型,其中保护鸟有引用函数时所有的信息。优点之一是,可以将函数句柄作为调用中的参量传递到另一个函数。
函数进一步有两种不同的类型,这两种类型都用函数句柄运算符@来创建。
例如:
>> f = @sin
f =
@sin函数sin可通过调用函数句柄f来间接调用:

第二个函数句柄的类型是匿名函数句柄,它由代替函数名的MATLAB表达式形成。构建你i名函数的通用格式是
@(input-argument-list) expression例如,如下匿名函数句柄可得到的输入的平方:
>> g = @(x) x.^2;匿名函数句柄的调用方式与名模函数句柄的调用方式类似。
单元矩阵提供了一种在意个变量名下组合一套对象(如数组、字符、其他单元矩阵)的方法。例如,假定我们正在处理:1、大小为512×512像素的uint8图像f;2、一个188×2数组的行形式的二维坐标序列b;3、包含两个字符名的单元数组char_array={‘area’, ‘centroid’}。这三个不同的实体可以使用单元数组组织成单一变量c:
C = {f, b, char_array}代码优化
预分配是指在进入以个计算数组元素的for循环之前,初始化数组。家当我们要创建一个MATLAB函数,计算
f(x) = sun(x/100π)
其中 ,x = 0,1,2…M-1.下面是第一种形式:
function y = sinfun1(M)
x = 0:M - 1
for k = 1:nume1(x)
y(k) = sin(x(k) / (100*pi));
end( numel(x)给出数组x的元素数 )
M = 5时的输出是

MATLAB函数tic和toc可用于测量函数执行的时间。调用tic,再调用该函数,再调用toc
>> tic; sinfun1(100); toc
时间已过 0.001127 秒。函数timeit可用于得到函数调用的可靠的、可重复的时间测量:
s = timeif(f)其中f是被及时函数的一个函数句柄,s是以秒计的相应调用f的测量时间
我们可以在M=100时对sinfun1用timeit来计时:
>> M=100
M =
100
>> f = @() sinfun1(M);
>> timeit(f)
ans =
2.9065e-05继续实验,用timeit测量sinfun1在M=500,1000,1500,·······,20000时的执行时间
M=500:500:20000;
for k = 1:numel(M)
f = @() sinfun1(M(k));
t(k) = timeit(f);
end这个时间会按照M^2的比例增长,每次都要重新分配新的内存空间,开销巨大。
预分配可以在逊克开始之前把它初始化为所下午的输出大小。通常用函数zeros来进行预分配。函数的第二张形式sinfun2.m使用预分配:
function y = sinfun2(M)
x = 0:M-1;
y = zeros(1, numel(x));
for k = 1:numel(x)
y(k) = sin(x(k) / (100*pi));
end