数模matlab入门教程-002-TSP问题通用建模方法与LINGO求解方法

数模matlab入门教程-002-TSP问题通用建模方法与LINGO求解方法

拿到题的第一刻，首先反应出这大概是个旅行商问题（TSP）。

1.旅行商问题简介

旅行商问题（Traveling Salemans Problem,TSP）也成货担郎问题。其是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等（摘自百度百科）。

2. TSP实例介绍

2.1 例题简介及邻接矩阵

举一个四个城市的简单例子，试题来自
（https://blog.csdn.net/Mind_V/article/details/74056277）
注：*试题虽然引用，但解法不同。

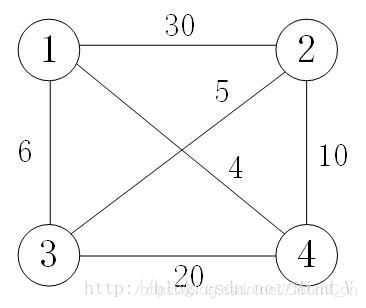
四个城市之间的距离邻接矩阵为：
AdjMat=[
0 30 6 4;
30 0 5 10;
6 5 0 20;
4 10 20 0
];

2.2 TSP一般建模方法

一般此类问题使用线性规划方法求解，也有个通用的建模方法，吾慢慢道来
通用建模方法：
设城市间的距离用矩阵d来表示，dij表示城市i与城市j之间的距离（这个d其实就是邻接矩阵AdjMat）。
设0-1矩阵X,用于表示经过的各城市之间的路线，定义如下
xij=0 路线并不从城市i到城市j
xij=1 路线为 城市i -> 城市j

考虑每个城市后只有一个城市，则

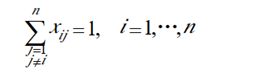
考虑每个城市前只有一个城市，则

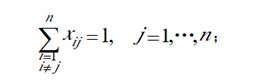
但仅以上约束条件不能避免在一次遍历中产生多于一个互不连通回路。 为此我们引入额外变量ui (i = 1,i…n），
附加以下充分约束条件：

三个约束目的在于保证不会点i和点j有回路。第三个约束解释为：

进而得到模型

以上问题可以用lingo进行求解，用lingo求解更为简单和方便：

关于LINGO教程，两篇文章入门
https://blog.csdn.net/breeze_blows/article/details/75332638
https://www.jianshu.com/p/a39b411ec367
吾不再赘述
代码为

MODEL:
SETS:
city/1..4/:u;
link(city,city):d,x;
ENDSETS
DATA:
d= 0 30 6 4
30 0 5 10
6 5 0 20
4 10 20 0 
;
ENDDATA
MIN=@SUM(link:d*x);
@for(city(j):@sum(city(i)|j#ne#i:x(i,j))=1);
@for(city(i):@sum(city(j)|j#ne#i:x(i,j))=1);
@for(link(i,j)|i#NE#j#and#i#gt#1:u(i)-u(j)+10*x(i,j)<=9);
@FOR(link:@BIN(x));

求解结果：

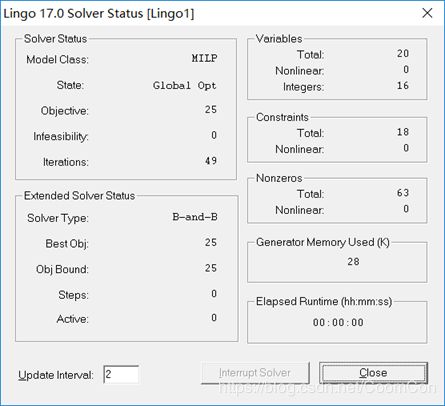
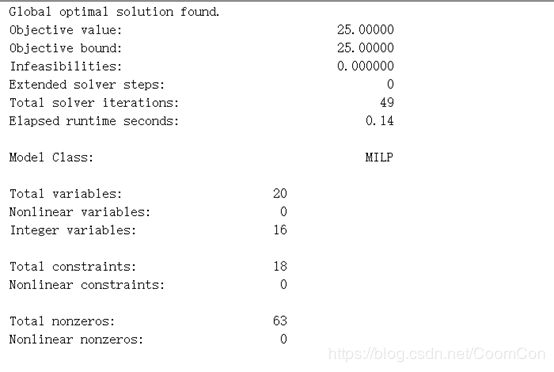
X( 1, 1) 0.000000 0.000000
X( 1, 2) 0.000000 30.00000
X( 1, 3) 0.000000 6.000000
X( 1, 4) 1.000000 4.000000
X( 2, 1) 0.000000 30.00000
X( 2, 2) 0.000000 0.000000
X( 2, 3) 1.000000 5.000000
X( 2, 4) 0.000000 10.00000
X( 3, 1) 1.000000 6.000000
X( 3, 2) 0.000000 5.000000
X( 3, 3) 0.000000 0.000000
X( 3, 4) 0.000000 20.00000
X( 4, 1) 0.000000 4.000000
X( 4, 2) 1.000000 10.00000
X( 4, 3) 0.000000 20.00000
X( 4, 4) 0.000000 0.000000
其中 X( 1, 4)，X( 2, 3)，X( 3, 1)，X( 4, 2) 等于1。
路线为1-4-2-3-1,费用为25。

原文求解路线为1,3,2,4,1 虽然先后不同，但走过的距离是一样的。

如有问题请联系公众号 一匹大懒虫