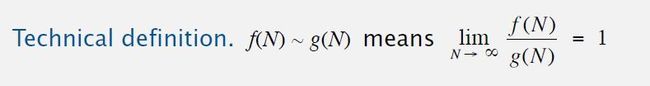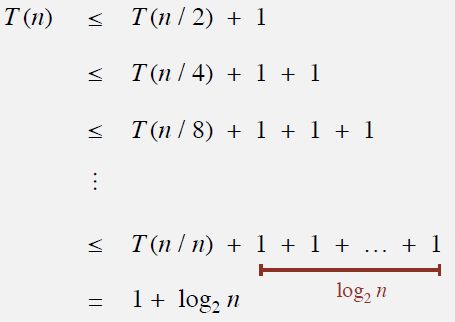前言
上一篇:并查集
下一篇:栈和队列
在算法性能上我们常常面临的挑战是我们的程序能否求解实际中的大型输入:
--为什么程序运行的慢?
--为什么程序耗尽了内存?
没有理解算法的性能特征会导致客户端的性能很差,为了避免这种情况的出线,需要具备算法分析的一些知识。
此篇主要涉及一些基础数学知识和科学方法,以及如何在实践应用中使用这些方法理解算法的性能。我们的重点放在获得性能的预测上。
主要分为5部分:
- 观察特点 (observations)
- 数学模型 (mathematical models)
- 增长阶数分类 (order-of-growth classifications)
- 算法理论 (theory of algorithms)
- 内存使用 (memory)
注:下文我所的增长量级和增长阶数是一个东西其实...
我们将从多种不同的角色思考这些问题:
- 程序员:解决一个问题,让算法能够工作,并部署它
- 用户:完成某项工作,但不关心程序做了什么
- 理论家:想要理解发生的事情
- 团队:可能需要完成以上角色的所有工作
关于算法分析需要集中考虑的关键是运行时间。运行时间也可以理解为完成一项计算我们需要进行多少次操作。
这里主要关心:
- 预测算法的性能
- 比较完成同一任务不同算法的性能
- 在最坏情况下算法性能的底线
- 理解算法如何运行的一些理论基础
算法分析的科学方法概述:
- 从自然界中观察某些特征(程序在计算机上的运行时间)
- 提出假设模型(与观察到的现象相一致的模型)
- 预测(利用上边的假设做出合理的预测,一般用来预测更大问题规模,或者另一台计算机上的运行时间)
- 验证(作更多的观察来验证我们的预测)
- 证实(重复地验证直到证实我们的模型和观察的特征吻合,证实我们的模型假设是正确的)
使用科学方法有一些基本原则:
- 别人做同样的实验也会得到相同的结果
- 假设必须具备某个特殊性质:可证伪性
(可证伪性:指从一个理论推导出来的结论(解释、预见)在逻辑上或原则上要有与一个或一组观察陈述与之发生冲突或抵触的可能。
可证伪,不等于已经被证伪;可证伪,不等于是错的。)
观察
第一步是要观察算法的性能特点,这里就是要观察程序的运行时间。
给程序计时的方法:
- 看表(你没看错,简单粗暴)
- 利用API:很多第三方或者Java标准库中有一个秒表类,可以计算用掉的时间
(如apache commons lang,springframework的工具包都有,这里使用stdlib库中的Stopwatch API 进行时间监控)
我们将使用 3-SUM 问题作为观察的例子。
3-SUM问题描述
三数之和。如果有N个不同的整数,以3个整数划为一组,有多少组整数只和为0.
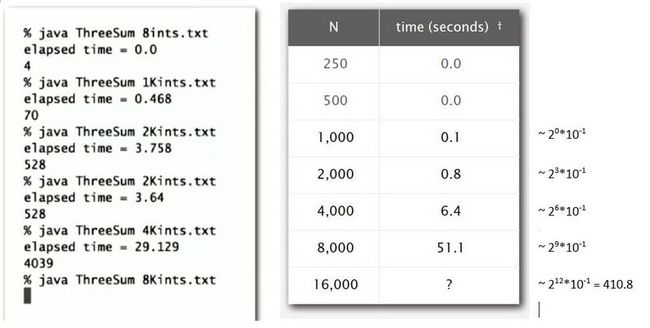
如下图,8ints.txt 有8个整数,有四组整数和为0
目标是编写一个程序,能对任意输入计算出3-SUM整数和为0有多少组。
这个程序实现的算法也很简单,首先是第一种,“暴力算法”
"暴力算法"
EN:brute-force algorithm
这里使用第三方API的方法测量程序运行的时间。
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.Stopwatch;
public class ThreeSum {
public static int count(int[] a) {
int N = a.length;
int count = 0;
//三重的for循环,检查每三个整数组合
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
for (int k = j + 1; k < N; k++)
//为了方便观察算法的性能问题,这里忽略了整型溢出问题的处理
if (a[i] + a[j] + a[k] == 0)
count++;
return count;
}
/**
* 读入所有整数,输出count的值
* 利用StopWatch执行时间监控
* @param args
*/
public static void main(String[] args) {
int[] a = StdIn.readAllInts();
Stopwatch stopwatch = new Stopwatch();
StdOut.println(ThreeSum.count(a));
double time = stopwatch.elapsedTime();
}
}实证分析
测试数据可以用越来越大的输入来运行。每次将输入的大小翻倍,程序会运行得更久。通过类似的测试,有时能相当方便和快速地评估程序什么时候结束。
数据分析
通过实证得出的数据,可以建立图像,使观察更直观:
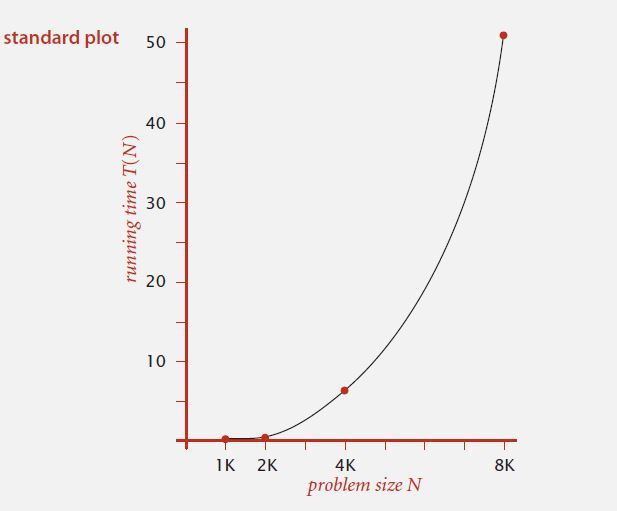
- 标准坐标 :Y轴:运行时间;X轴:输入大小
- 双对数坐标:Y轴:取运行时间的对数;X轴:取问题输入大小的对数
(lg以2为底)
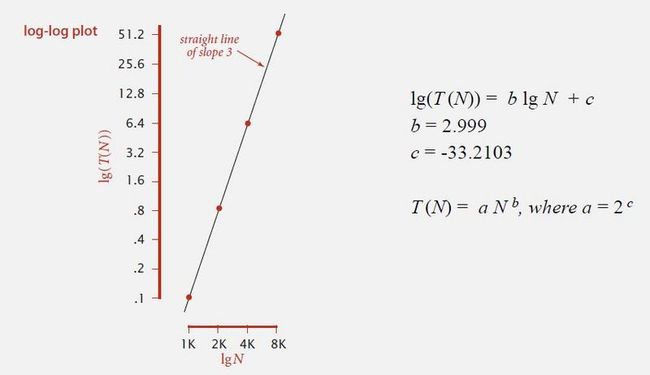
使用双对数坐标通常情况下是得到一条直线,这条直线的斜率就是问题的关键。
这个例子(3-SUM 暴力算法)的斜率是3
--通过对数坐标的方法得出公式:lg(T(N)) = blgN + c (可看做 y = b*x + c,其中 y = lg(T(N)),x = lgN)
--通过图中两点可求出b,c值,如果等式两边同时取2的幂,就得到 T(N) = 2^c*N^b, 其中 2^c 为一个常数,可记作 a
由此,从这个模型的观察中我们就得到了程序的运行时间,通过一些数学计算(在这里是回归运算),我们就知道得出了运行时间:
T(N) = a*N^b (b为双对数坐标中直线的斜率,同时 b 也是这个算法的增长量级,第三点会讲到)
预测和验证
假设
通过上述的数据分析,我们得出假设:
运行时间看起来大约是 1.006 × 10^–10 × N^2.999 (秒)
预测
可以运用这个假设继续做预测,只要带入不同的N值,就能计算出需要的大致时间。
・51.0 seconds for N = 8,000.
・408.1 seconds for N = 16,000.
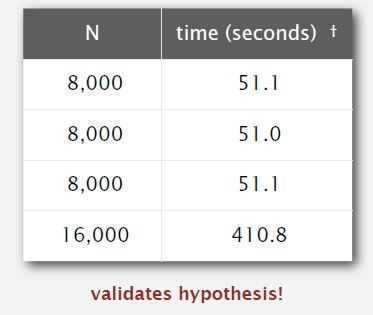
验证
通过对比 程序实际运行时间(下图) 和 通过我们的假设模型预测的时间上一步) 可以看出结果非常相近 (51.0 vs ~51.0/408.1 vs ~410.8)
这个模型帮助我们在不需要花时间运行试验的前提下做一些预测。实际上这个情形中存在幂定律(a*N^b).实际上绝大多数的计算机算法的运行时间满足幂定律。
下边介绍一种求解符合幂定律运行时间中的增长量级值(b)的方法
Doubling hypothesis 方法
- 计算b值
这里可以通过 Doubling hypothesis 的方法可以快速地估算出幂定律关系中的 b 值:
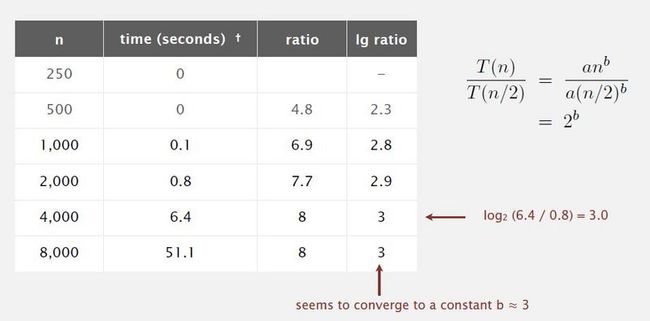
运行程序,将每次输入的大小翻倍(doubling size of the input),然后计算出N和2N运行时间的比率。主要看下图的后几行运算时间比率,前几行的输入值小,以现在的计算机运算能力处理起来,立方级别的增量级运算速度快也相差无几。
ratio ≈ T(2N)/T(N)
至于为什么 0.8/0.1≈7.7 或其他看起来 "运算错误" 类似的情况,是因为图上的运行时间的记录是简化精确到了小数点后一位,实际运算比率值是使用了实际运行时间(精确到小数点后几位)去计算的,所以会出现0.8/0.1≈7.7。
通过不断地进行双倍输入实验,可以看到比率会收敛到一个常数(这里为8),而实际上比率的对数会收敛到N的指数,也就是 b 的值,这里粗暴算法的 b 值就等于3
通过Doubling hypothesis方法我们又能提出假设:
此算法的运行时间大约是 a*N^b, 其中 b = lg ratio
注意:Doubling hypothesis 不适用于识别对数因子
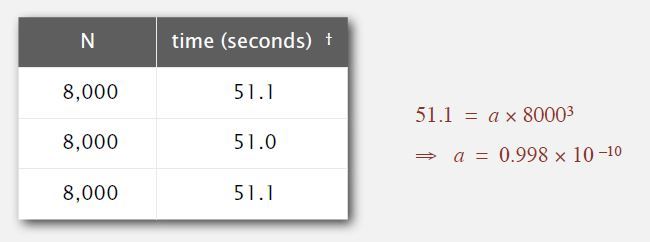
- 计算a值
得出 b 的值后,在某个大的输入值上运行程序,就能求出 a 值。
由此得出假设:运行时间 ≈ 0.998 × 10^–10 × N^3 (秒)
我们通过作图得出的模型( ≈ 1.006 × 10^–10 × N^2.999 )和我们通过Doubling hypothesis方法得出的模型是很接近的。
计算机中有很多的因素也会影响运行时间,但是关键因素一般和计算机的型号无关。
影响因素
关键的因素即为你使用的算法和数据. 决定幂定律中的 b 值
还有很多与系统相关的因素:
- 硬件配置:CPU,内存,缓存...
- 软件环境:编译器,解析器,垃圾回收器...
- 计算机的系统:操作系统,网络,其它应用...
以上所有因素,包括关键因素,都决定了幂定律中的 a 值
现代计算机系统中硬件和软件是非常复杂的,有时很难获得非常精确的测量,但是另一方面我们不需要像其他科学中需要牺牲动物或者向一颗行星发射探测器这些复杂地方法,我们只需要进行大量的实验,就能理解和得到我们想要知道的影响因子(的值)。
数学模型
通过观察发生了什么能够让我们对性能作出预测,但是并不能帮助我们理解算法具体做了什么。通过数学模型更有利于我们理解算法的行为。
我们可以通过识别所有的基本操作计算出程序的总运行时间。
致敬一下,Don Knuth 在二十世纪60年代末便提出和推广了运行时间的数学模型:sum(操作的开销 * 操作执行的频率)
- 需要分析程序以确执行了哪些操作。
- 计算机以及系统的开销取决于机器,编译器。
- 频率分析将我们引向数学方法,它取决于算法,输入数据。
基于 knuth 研究得知,原则上我们能够获得算法,程序或者操作的性能的精确数学模型。
基本操作的开销
基本操作的开销一般都是一个取决于计算机及系统的常量,如果想要知道这个常量是多少,可以对一个基本操作运行成千上万的实验的方式算出。比如可以进行十亿次的加法,然后得出在你运行的计算机系统上进行 a + b 的基本操作花费大概 2.1 纳秒
为了方便建立数学模型,绝大多数的情况下我们只要 假定它是某个常数 cn (n:1,2,3...) 就可以。
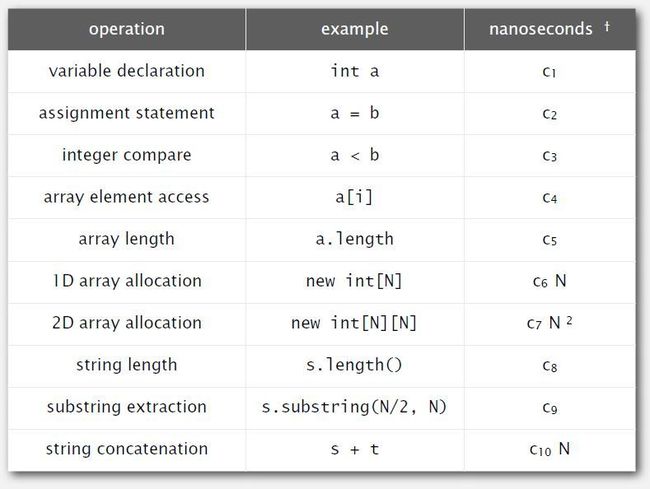
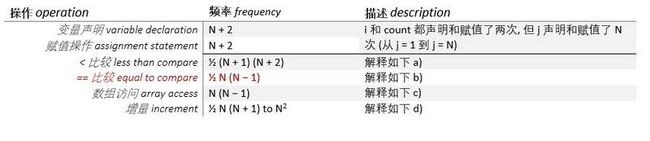
下图罗列了一下基本操作和其开销
关于N:当我们在处理一组对象时,假设有N个对象,有一些操作需要的时间和N成正比。比如第六行,分配一个大小为N的数组是,需要正比于N的时间,因为在Java中默认吧数组中的每个元素初始化为0.
还有些运行时间去决定系统的实现,比如连接两个字符串需要的运行时间与字符串的长度(N)成正比,连接字符串并不等同于加法运算
操作执行的频率
- 1-SUM 为例
数组中有多少个元素等于0
public class OneSum {
public static int count(int[] a) {
int N = a.length;
int count = 0;
for (int i = 0; i < N; i++)
if(a[i] == 0)
count++;
return count;
}
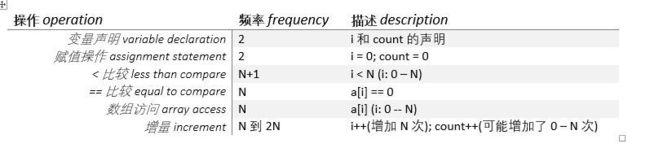
}其中几项操作的频率取决于N的输入
- 2-SUM 为例
数组中有多少对元素等于0
public class TwoSum {
public static int count(int[] a) {
int N = a.length;
int count = 0;
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
if (a[i] + a[j] == 0)
count++;
return count;
}
}额外稍微解释下数据怎么算来的,如果已经了解可以略过以下细致的解释。
j 每次迭代的增量都取决于 i 的值,因为 j 被初始化为 i + 1
便于理解可以用具体数值带入:
假设 N = 5
当 i == 0 时,i 递增到 1,递增了 1 次;j 从 1 递增到 5,递增了4次;i 和 j 一起递增了 5 次
当 i == 0 时,i 进行了 1 次 i < N 的比较,j 进行了 5 次 j < 5 的比较,i 和 j 一起进行了 6 次比较
将具体泛化:
a) < 比较 : 离散求和公式:0 + 1 + 2 +...+ N + (N+1) = ½(N+1)(N+2)
即当 i == 0 时,j < N 的比较会进行 N 次,因此总的来说,i 的第一次迭代中**i和j**一起有 N + 1 次比较操作
而后 i 递增,对于 i == 1 的下一次迭代,j < N 进行了 N - 1 次,在i的第二次迭代中,**i和j一起**有N次比较操作
即 i 每加 1,j 都会在上一层比较的基础上少比较一次
直到 i == N, j 不再进行比较操作,i 和 j 一共有 1 次比较操作
i + j 总共进行 < N 比较操作的频率利用离散求和就是½(N+1)(N+2)
b) == 比较 : 离散求和:0 + 1 + 2 +...+ (N-2) + (N-1) = ½ N (N − 1)
即当 i == 0 时,j 将会迭代 N-1 (从1到N-1) 次
而后 i == 1 时,j 将会迭代 N-2 (从2到N-1) 次
当 i == N 时,j 将不会再迭代,即 0 次结束
即 i 每加 1,j 都会在上一层迭代的基础上少迭代一次
利用离散求和得出 j 的迭代次数为 ½ N (N − 1)
j 的 迭代频率与进行“==”比较的操作频率是一样的,所判断相等的操作频率就等于½ N (N − 1)
c) 数组访问 : 假设我们假设编译器/JVM没有优化数组访问的情况下
每次进行相等比较都会有两次数组访问的操作,所以是½ N (N − 1) * 2 = N (N − 1)
d) 增量{++} : ½ N(N+1) to N^2.,coursera上ppt的½ N (N − 1) to N (N − 1)是错的
Mathematical Models, slide 28, 30, 32. Number of increments should be ½ N(N+1) to N^2.
(参见coursera 课程勘误表Resources--Errata)
当 i == 0 时,i 先进行递增,j 也递增了 N-1 次,因此总的来说,i 的第一次迭代中**i和j**一起有 N 个递增
然后i递增,对于 i == 1 的下一次迭代,j 将递增 N-2 次,在i的第二次迭代中,**i和j一起**给出N-1个增量。
一直到 i == N,**i和j一共**只有一次递增 (j 不再递增)
同样利用离散求和:N +(N-1)+ ... + 2 + 1,**i和j一起给出** ½N(N+1)个增量
下限 : ½ N(N+1)(假设计数完全没有增加,即count没有增加,只有上诉 i 和 j 进行了增量)。
上限 : 我们假设计数器count在每次循环都增加,count++执行的次数与“等于比较”的次数相同,因此我们得到 ½ N(N+1) + ½ N(N-1) = N^2
数学表示的简化
- 第一种简化
原则上我们是可以算出这些精确的次数,可是这样太繁琐。图灵大佬1947年就提出了,其实我们测量计算过程中的工作量时不用列出所有细节,粗略的估计同样有用。其实我们只需要对开销最大的操作计数就OK了。所以现在我们也这么干。我们选出开销最大的基本操作,或者是执行次数最多的、开销最大的、频率最高的操作来代表执行时间。
我们假设运行时间等于 常数*操作的执行时间,在 2-SUM 例子中,
我们选择访问数组的时间 (c*N(N − 1)) 代表这个以上算法的运行时间。
- 第二种简化
-- 估算输入大小为 N 的函数的运行时间(或内存)
-- 忽略推导式子中的低阶项。使用 tilde notation (~ 号)表示:
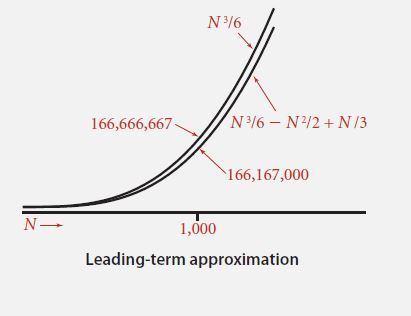
a) 当 N 很大时,我们只需要关注高阶项的开销
b) 当 N 很小时,虽然低阶项不能忽略,但是我们更无需担心,因为小 N 的运行时间本来就不长,我们更想要对大 N 估计运算时间
如图,当 N 很大时,N^3 远比后边的 N 的低阶项要大得多,大到基本不用关注低阶项,所以这些式子都近似为 (1/6)N^3
波浪号的含义:f(n) 近似于 g(n) 意味着 f(n)/g(n)的极限等于 1
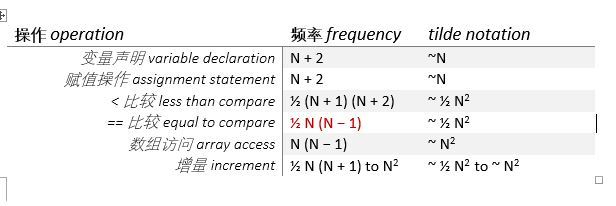
简化统计频率后,我们可以这么样的表示:
是不是看起来更微妙,更清爽~
结合两种简化,我们就可以说 2-SUM 需要近似 N^2 次数组访问,并暗示了运行时间为 ~c*N^2 (c 为常数)
利用开销模型和 ~ 尝试对 3-SUM 问题进行分析
- 3-SUM 为例
public class ThreeSum {
public static int count(int[] a) {
int N = a.length;
int count = 0;
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
for (int k = j+1; k < N; k++)
if (a[i] + a[j] + a[k] == 0)
count++;
return count;
}
}
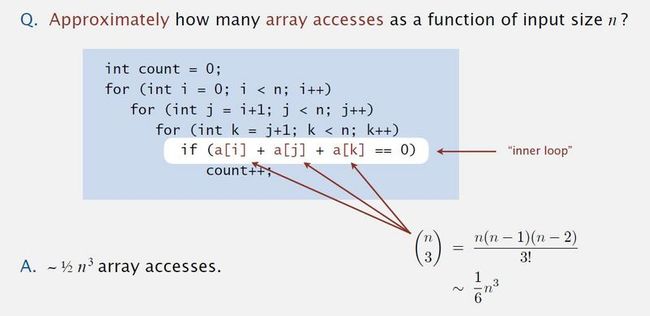
开销最大的就是这句了:if (a[i] + a[j] + a[k] == 0),我们可以说 3-SUM 问题需要近似 ~ ½ n3 次数组访问,并暗示了运行时间 ~½ c*n3 (c 为常数)
为了避免部分蒙圈现象,解释下为什么是1/6 N^3 和 1/2 N^3
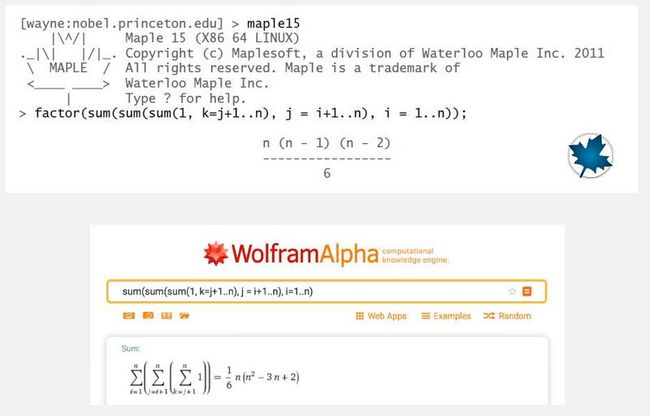
a) 1/6 N^3 这个值还是离散求和得出的,可以参考 2-SUM. 就是又多了一层loop. 建议利用计算器或者工具去计算
Maple 或者 Wolfram Alpha
b) 因为 1/6 N^3 是 equal to compare 的次数,不是数组访问的次数。
每次在执行 equal to compare 都有 3 次数组访问,所以是 1/6 N^3 * 3 = 1/2 N^3
小节总结
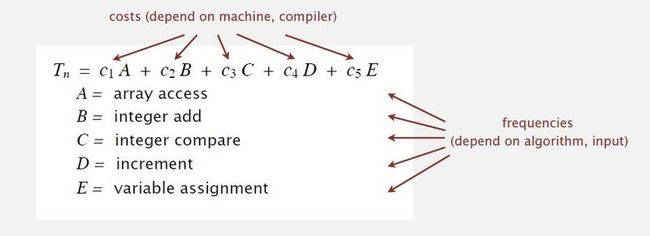
精确的模型最好还是让专家帮搞定,简化模型也是有价值的。有时会给出一些数学证明,但是有时候引用专家的研究成果,利用数学工具就可以了。简化后我们就不用去计算所有操作的开销,我们选出开销最大的操作乘上频率,得出适合的近似模型来描述运行时间。精确一点的数学模型如下:
costs:基本操作的开销,常量,取决于计算机,编译器
frequencies:操作频率,取决于算法,输入大小(即 N 的大小)
增长量级分类
以下增长量级同增长阶数一个意思。
概述
增长量级可以看做是函数类型,如是常量,线性函数,指数函数,平方,立方,幂函数等。
一般分析算法时我们不会遇到太多不同的函数,这样我们可以将算法按照性能随问题的大小变化分类。
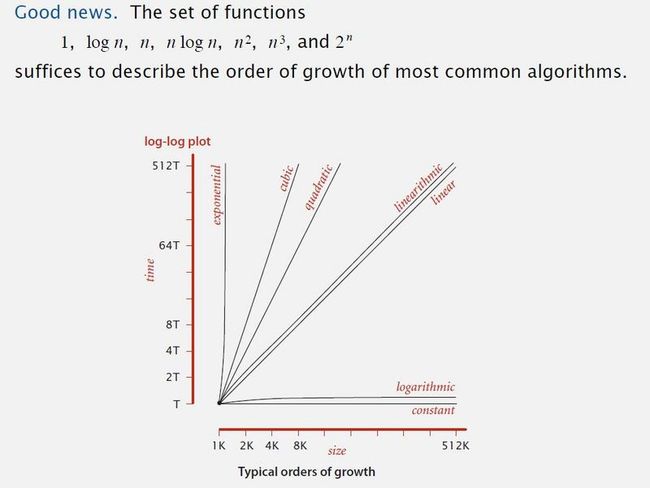
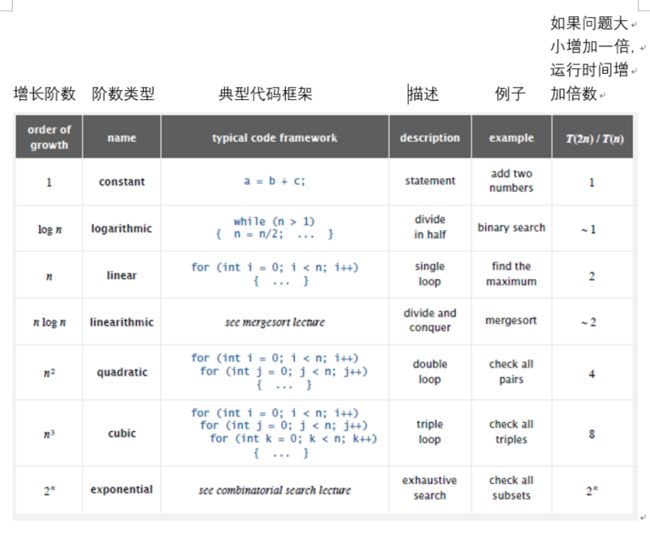
一般算法我们都能用这几个函数描述:
当我们关注增长量级时,我们会忽略掉函数前面的常数。比如当我们说这个算法的运行时间和 NlogN 成正比,等同于我们假设运行时间近似 cNlogN (c 为常数).
上图为双对数坐标图,从图中可以看出如果:
- 增长量级是对数(logarithmic)或者常数(constant),无论问题的规模多大,算法的运行速度都很快
- 增长量级是线性的(linearithmic/linear), 也就是增长量级与问题大小N成正比,N增长,运行时间也会随问题规模大小线性增长 (NlogN 就是 linearithmic 类型的增长量级)
以上两种算法都是我们想要设计的算法,它们能够成比例适应问题的规模。
- 增长量级为平方阶(quadratic),运行时间远快于问题输入的大小,即 N 的大小。这种算法不适合处理庞大问题的输入。立方阶(cubic)的算法就更糟糕
- 还有一种指数阶算法(exponential),出来庞大输入也不会用到
综上所诉,我们研究算法是,首先要保证这些算法不是平方或者立方阶的。
增长阶数类型实际上就源于我们写的代码中的某些简单模式。下图使用翻倍测试(参考上边 Doubling hypothesis 内容)得出算法运行时间随问题大小翻倍后增长的翻倍情况。某些增长量级对应的代码模式如下:
- 如果没有循环,增长阶数是常数(constant),运行时间的增长是常数的;
-
如果有某种循环:
- 每次循环被分为两半(如二分查找算法 binary search),增长阶数就是对数,运行时间的增长几乎是常数的
- 如果遍历了输入中的所有对象,运行时间是线性的(与 N 成正比),典型的例子是找一个数组里头的最大值,或是上边提到的 1-SUM 问题
- nlogn 线性对数阶算法,这种时间复杂度源于一种特定的算法设计技巧叫分治法,如归并排序(mergesort),后续几周内会有介绍
- 算法中有两层for循环(如 2-SUM),算法的运行时间是平方阶的,和N^2成正比,当输入翻倍后,运行时间增大4倍
- 三层loop(如 3-SUM),运行时间就是立方阶的,与N^3成正比,当输入翻倍后,运行时间增大8倍
- 指数阶算法 2^n, 运行时间是指数阶,这些算法中的涉及到的 N 都不会非常大
通过上述分析,我们在设计处理巨大规模输入的算法的时候,一般都尽量把算法设计成线性阶数和线性对数阶数。
为了展示描述算法性能的数学模型的建立过程,下边以 binary search 二分查找为例
Binary search 二分查找
算法介绍
目标:给定一个有序整数数组,给定一个值,判断这个值在这个数组中是否存在,如果存在,它在什么位置
二分查找:将给定值与位于数组中间的值进行比较
- 比中间值小,向中间值左边查找
- 比中间值大,向中间值右边查找
- 相等即找到
如下图,查找 33,首先和 53比较,33<53, 所以如果33存在,那么就会在数组的左半边,然后递归地使用同样的算法,直到找到,或确认要查找的值不在给定数组中。下图展示二分查找的过程(使用了3个指针 lo, hi, mid)
初始化 lo 指针指向 id[0], hi 指针指向 id[n-1], mid 指针指向 id[mid]
33<53, hi指针向左移动到mid的前一位
33>53, lo 指针向右移动到mid的后一位
33<43, hi 指针移动到 43 之前,也就是数组中 33 的位置,此时只剩下一个元素查看,如果等于 33,则返回 index 4, 如果不等于 33,则返回 -1,或者别的形式说明要查找的定值不在数组中
Java 实现
此算法的不变式:如果数组 a[] 中存在要寻找的关键字,则它在 lo 和 hi 之间的子数组中, a[lo] ≤ key ≤ a[hi].
public static int binarySearch(int[] a, int key)
{
int lo = 0, hi = a.length - 1;
while (lo <= hi)
{
//why not mid = (lo + hi) / 2 ?
int mid = lo + (hi - lo) / 2;
//关键值与中间值是三项比较(<,>, ==)
if (key < a[mid]) hi = mid - 1;
else if (key > a[mid]) lo = mid + 1;
else return mid;
}
return -1;
}
数学分析
定理:在大小为 N 的有序数组中完成一次二分查找最多只需要 1 + lgN 次的比较
定义:定义变量 T(N) 表示对长度为 N 的有序数组的子数组(长度<=N)进行二分查找所需要的比较次数
递推公式(根据代码):T(n) ≤ T(n / 2) + 1 for n > 1, with T(1) = 1.
程序将问题一分为二,所以T(n) ≤ T(n / 2) 加上一个数值,这个数值取决于你怎么对比较计数。这里看做二向比较,分成两半需要进行一次比较,所以只要 N>1, 这个递推关系成立。当 N 为 1 时,只比较了 1 次。
裂项求和
我们将递推关系带入下面公式右边(即 <= 号右边)求解,
如果T (n) ≤ T (n / 2) + 1 成立,则 T (n / 2) ≤ T (n / 4) + 1 成立...
这个证明虽然是证明在 N 是 2 的幂的时候成立,因为并没有在递推关系中明确 N 是奇数的情况,但是如果把奇数情况考虑进来,也能够证明二分查找的运行时间也总是对数阶的。
基于这个事实,我们能够对 3-SUM 问题设计一个更快的算法:
3 - SUM 举例
(基于增长量级与二分查找应用)
Java 实现:
import java.util.Arrays;
public class ThreeSumFast {
// Do not instantiate.
private ThreeSumFast() { }
// returns true if the sorted array a[] contains any duplicated integers
private static boolean containsDuplicates(int[] a) {
for (int i = 1; i < a.length; i++)
if (a[i] == a[i-1]) return true;
return false;
}
/**
* Prints to standard output the (i, j, k) with {@code i < j < k}
* such that {@code a[i] + a[j] + a[k] == 0}.
*
* @param a the array of integers
* @throws IllegalArgumentException if the array contains duplicate integers
*/
public static void printAll(int[] a) {
int n = a.length;
Arrays.sort(a);
if (containsDuplicates(a)) throw new IllegalArgumentException("array contains duplicate integers");
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
int k = Arrays.binarySearch(a, -(a[i] + a[j]));
if (k > j) StdOut.println(a[i] + " " + a[j] + " " + a[k]);
}
}
}
/**
* Returns the number of triples (i, j, k) with {@code i < j < k}
* such that {@code a[i] + a[j] + a[k] == 0}.
*
* @param a the array of integers
* @return the number of triples (i, j, k) with {@code i < j < k}
* such that {@code a[i] + a[j] + a[k] == 0}
*/
public static int count(int[] a) {
int n = a.length;
Arrays.sort(a);
if (containsDuplicates(a)) throw new IllegalArgumentException("array contains duplicate integers");
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
int k = Arrays.binarySearch(a, -(a[i] + a[j]));
if (k > j) count++;
}
}
return count;
}
/**
* Reads in a sequence of distinct integers from a file, specified as a command-line argument;
* counts the number of triples sum to exactly zero; prints out the time to perform
* the computation.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
In in = new In(args[0]);
int[] a = in.readAllInts();
int count = count(a);
StdOut.println(count);
}
} 基于搜索的算法:
- 第一步: 将输入中的数进行排序(排序算法后边会做介绍)
- 第二步: 查看每对数字 a[i] 和 a[j], 对 - (a[i] + a[j]) 进行二分查找.
如果找到- (a[i] + a[j]),那么就有 a[i], a[j] 和 - (a[i] + a[j]) 三个整数和为 0
运行时间的增长阶数: N^2 log N.
- 第一步: 排序需要正比于 N^2(如果使用插入排序, N^2的数组访问还是好理解的,两层loops).
-
第二步: 二分查找使用 N^2 log N
- 主要看这里:
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
int k = Arrays.binarySearch(a, -(a[i] + a[j]));
if (k > j) count++;
}
} 第2步进行多次二分搜索。多少次? N ^ 2次。二分查找需要log(n)时间 (请参考概述中最后一个表和回顾二分查找的内容)。
因此,循环需要(N ^ 2 * log(N))时间。
应该注意循环在排序后发生。不在排序过程中发生。由于操作一个接一个地发生,我们添加了运行时间。不是成倍增加。
**总运行时间是这样的**:
(N ^ 2)+(N ^ 2 * log(N))
**由于忽略了较低阶项**,因此算法只有最重要的项的增长顺序:
(N ^ 2 * log(N))
通常,更好的增长阶数意味着程序在实际运行中更快。
为了更有说服力,一般情况下不考虑上下限问题,运行时间为最坏情况下的时间复杂度 (算法理论内容)
算法理论
增长量级在实际运用在是非常重要的,它直接反映了算法的效率,近年来人们针对增长量级也做了很多研究。
分析类型:性能取决于输入
一个不同的输入可能会让算法的性能发生巨大变化。我们需要从不同的角度针对输入的大小分析算法。运行时间介于最好情况与最坏情况之间。
Best case:最好情况,算法代价的下限(lower bound on cost), 运行时间总是大于或等于下限。
- 由“最简单”的输入决定
- 为所有输入情况提供目标 (应对所有输入,希望运行时间能够是或者接近最好情况)
Worst case:最糟糕的情况,算法代价的上限(Upper bound on cost), 运行时间不会长于上限。
- 由“最复杂”的输入决定
- 为所有输入提供担保 (最坏的情况的分析结果为我们提供底线,算法运行时间不会长于这种情况)
Average case:平均随机情况,将输入认为是随机的
- 需要以某种方式对问题中的随机输入进行建模
- 提供预测性能的方法
一般的,即使输入变化非常大,我们也能够各种情况进行建模和预测性能
Ex 1. 如上边的 3-SUM 问题:
通过“暴力算法”,数组的访问次数为
Best: ~ ½ N^3
Average: ~ ½ N^3
Worst: ~ ½ N^3
其实各种情况的低阶项是不一样的,但是因为我们利用了简化方法忽略了低阶项(回顾数学表示的简化内容),所以3种情况下的数组访问几乎是一样的。使用近似表达时,算法中唯一的变化就是计数器 count 增加的次数。
Ex 2. 二分查找中的比较次数
Best: ~ 1 常数时间,第一次比较结束后就找到了关键字
Average: ~ lg N
Worst: ~ lg N
应对不同的输入,我们有不同的类型分析,但是关键是客户要解决的实际问题是什么。为了了解算法的性能,我们也要了解这个问题。
实际数据可能与输入模型不匹配怎么办?
- 需要了解输入以有效地处理它
-
方法1:取决于最坏情况下的性能保证,保证你的算法在最坏情况下运行也能很快
- 示例:使用归并排序 Mergesort 而不是快速排序 Quicksort
如果不能保证最坏情况,那么就考虑随机情况,依靠某种概率条件下成立的保证
-
方法2:随机化,取决于概率保证。
- 示例:Quicksort
(排序在后几个星期有谈论到)
对于增长量级的讨论引出了对算法理论的讨论
算法理论 - 探讨最坏情况
新目标
-
确定问题的“困难性”
- 例如 3-SUM 有多难?
- 开发“最优”算法解决问题
方法
用增长量级对最坏情况进行描述
- 在分析中试着去掉尽可能多的细节,将分析做到只差一个常数倍数的精度,这就是上边所说到的利用增长量级分析的方法
- 通过关注最坏的情况,完全忽略输入模型,消除输入模型的可变性,把重点放在针对最坏情况的设计方法上,这样就能简便地只利用增长阶数来谈论算法性能
分析的目标是找出“最优”算法
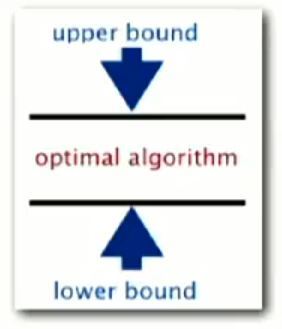
最优算法
- 对于任意输入,我们能将运行时间的浮动控制在一个常数之内。
- 因为是针对最坏情况考虑,所以提出的算法也就证明了除了它以外,没有其它的算法提供更好的性能保证了,这个算法就是“最优的”
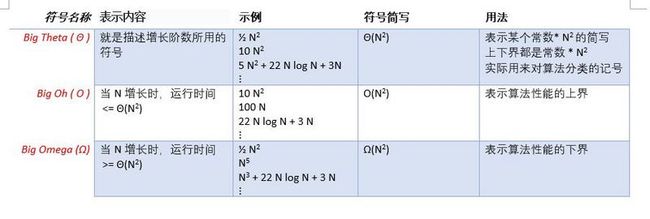
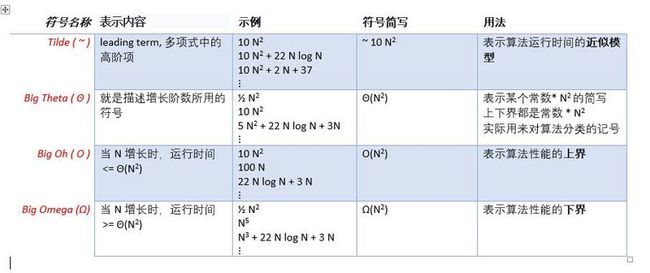
描述性能界限的常用记号
如何使用这三个符号对算法按照性能分类?
使用示例
1-SUM 问题
目标:确定问题的“难度”并开发“最优”算法。
- EX. 1-SUM 问题:数组中是否有0?
上限:O(g(N)) 问题难度的上限取决于某个特定的算法
- EX. 1-SUM的暴力算法:查看每个数组元素
- 暴力算法的运行时间为 Θ(N)
-
1-SUM 问题未知的最优算法的运行时间是 O(N):
- 这里的 g(N)=N,重复一次,Θ(N) 表示某个常数*N。暴力算法已经表明解决 1-SUM 问题需要 Θ(N) 的时间,那么如果存在最优算法,运行时间肯定是 ≤ Θ(N), 根据上表,≤ Θ(N) 用 O(N) 表示
下限:Ω(h(N)) 证明没有算法可以做得比 Θ(h(N)) 更好了
- Ex. 必须检查所有N个数组里头的元素(任何未经检查的条目都可能为0)
-
1-SUM 的未知最优算法的运行时间是 Ω(N)
- 这里 h(N) = N,因为必须检查所有项,没有别的算法可以做到比暴力算法 Θ(N) 更好了,所以 1-SUM 的未知最优算法的运行时间是肯定都是 ≥ Θ(N) 的,记作 Ω(N)
最优算法:
- 下限等于上限:g(N)= h(N)= N
- Ex. 1-SUM 的暴力算法是最优的:其运行时间是 Θ(N)。
对于简单问题,找到最优算法还是比较简单的,但对于很复杂的问题,确定上下限就很困难,确定上下界吻合就更加困难。
3-SUM 问题
目标
- 确定问题的“难度”并开发“最优”算法。
- Ex. 3-SUM: 数组中,三个数和为 0 出现多少次
暴力算法分析
上限: 问题难度的上限取决于某个特定的算法
- Ex. 3-SUM 的暴力算法
-
3-SUM 的最优算法的运行时间为 O(N^3)
- 3-SUM 的的暴力算法需要的运行时间是 Θ(N^3),如果存在某种算法比暴力算法更优,那么运行时间肯定 ≤ Θ(N^3), 记作 O(N^3)
但如果我们找到了更好的算法
上限: 一种特定的改进算法
- Ex. 改进的 3-SUM 算法
- 3-SUM 最优算法的运行时间为 O(N^2*logN) {使用了二分查找}
下限: 证明没有别的算法可以做得更好
- Ex. 必须检查所有N个条目以解决 3-SUM 问题
- 求解 3-SUM 的最优算法的运行时间为 Ω(N)
可能大家还是对Omega Ω 符号有点困惑。 Omega只显示算法复杂度的下限。 3-SUM 算法需要检查来自某个数组的所有元素,因此我们可以说,该算法具有 Ω(N) 复杂度,因为它至少执行线性数量的操作。事实上,操作总数是更大的,因此实际最优算法肯定是 ≥ Θ(N) 的,记作 Ω(N)
对于 3-SUM 问题没有人知道更高的下界,其实我们现在就能看出,处理 3-SUM 问题肯定是要用超过 Θ(N) 的时间的,但是我们却不能确定多出多少,就是不知道比 Θ(N) 更高的下界是多少。
当有人证明更高的下限时,也是同意没有算法可以做得比前一个下限更好的前提下提出新的下界。但是他们会做出了更强有力的陈述,特别是证明没有算法可以实现比他们刚才证明的新下界更好,以此来提高原来的下界,定义一个新的下界。
新的下限可能仅略高于先前的下限,或者可能显着更高。提高下界往往都不是很容易。谈论如何提高下界这也不是本文的重点。
算法理论中的一个开放问题:
·3-SUM 有最优算法吗?我们不知道
·3-SUM 问题是否存在一个运行时间小于 O(N^2) 的算法?我们无法确定
·3-SUM 比现行的下界更高的下界是什么,上面已经谈论过了,我们也还不知道
我们不知道求解 3-SUM 问题的难度
算法设计的方法
- 遇到新的问题,设计出某个算法,并证明它的下界
- 如果上界和下界存在间隔,那么寻找新的能够降低上界的算法,或者是寻找提高下界的方法(但是这个一般很难)
所以人们更倾向于研究持续下降上界,也就是设法提高算法在最坏情况下的运行时间来了解问题的难度,并得到了很多最坏情况下的最优算法。
- 这门课程并不会把注意点都放在关注最坏的情况去分析算法性能,而是专注于理解输入的性质(不一定是最糟糕的情况),并针对输入的性质寻找最高效的算法
- 真的要预测性能和比较算法时,我们需要比常数因子级别误差更准确的分析
值得注意的是:有很多人错把 big-Oh 分析结果当做了运行时间的近似模型,其实 big-Oh 应该是这个问题运行时间的上界,不是运行时间的近似模型。
我们使用 ~ 来表示算法运行时间的近似模型。当我们谈论到运行时间的上界就使用 big-Oh.
内存使用
运行时间和程序的内存需求都会对算法的性能有所影响,下边是对内存需求的简单讨论。
从根本上讲我们就是想知道程序学要多少比特(bit),或者多少字节(byte)
Bit: 0 or 1
Byte: 8 bites
Megabyte (MB) 2^20 bytes
Gigabyte (GB) 2^30 bytes.
32-bit machine: 32 位系统,指针是 4 个字节,
64-bit machine: 64 位系统,指针是 8 个字节,这使得我们能够对很大的内存寻址,但是指针指针也使用了更大的空间。有些 JVM 把指针压缩到 4 bytes 来节省开支。
典型的内存使用量
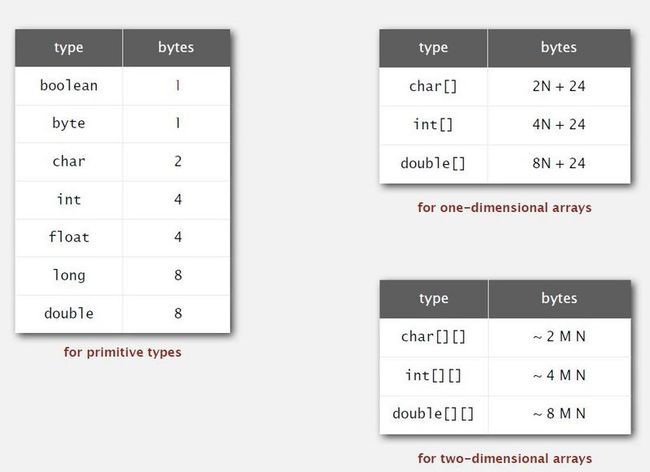
内存使用和机器还有硬件实现有很大的关系,但是一般情况都是如图所示
Boolean 虽然只用了 1 bit,但系统还是分配了 1 byte 给它
数组需要额外空间 + 基本类型空间开支(参考左表) * 元素个数(N)
二维数组需要的空间下图用近似值表示, ~ 2MN 可以理解为 char 基本类型开销是 2 bytes,char [M] [N] 近似用了 2MN bytes 的内存
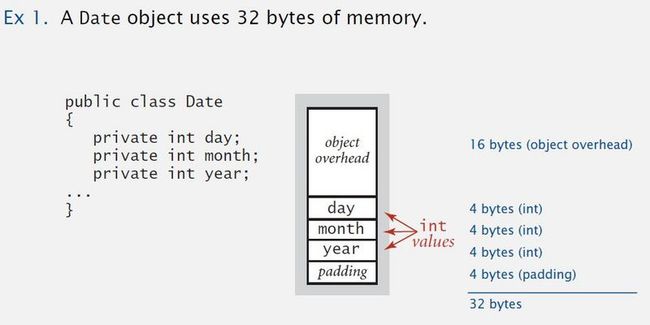
典型的 JAVA 对象内存开销
Object overhead 对象需要的额外空间. 16 bytes.
Reference 引用. 8 bytes.
Padding 内置用来对齐的空间. 对齐空间可以是 4 bytes 或者是其它,对齐空间的分配目的是使得每个对象使用的空间都是 8 bytes 的倍数
下图是一个日期对象的内存占用量例子
数据类型值的总内存使用量:
- 基本数据类型:int 为 4 字节,double 为 8 字节,...
- 对象引用:8个字节,这是指针需要占用的空间
- 数组:24 个字节 + 每一项的内存。
- 对象:16 个字节 + 实例变量的空间 ( + 8个字节,如果有内部类对象)
- 对齐空间:增加一定量字节,使得上边的字节加上这里的字节数和为 8 个字节的倍数
例子:用了多少字节?
使用上边的基本知识可以算出 B
- 对象的额外空间 16 bytes (参考日期对象用例)
- int[] id:8 byte + ( 4N + 24 )
- int[] sz:同上 (引用 + 24 个字节 + int 类型开销 * N)
- int count:4 bytes
- 对齐空间:4 byte
总共 8N + 88 ~ 8 N bytes.
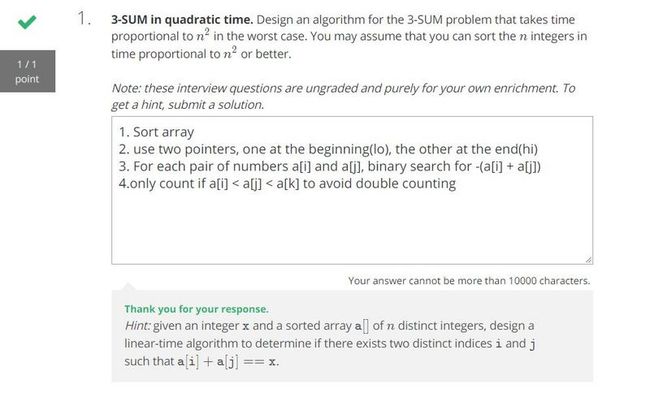
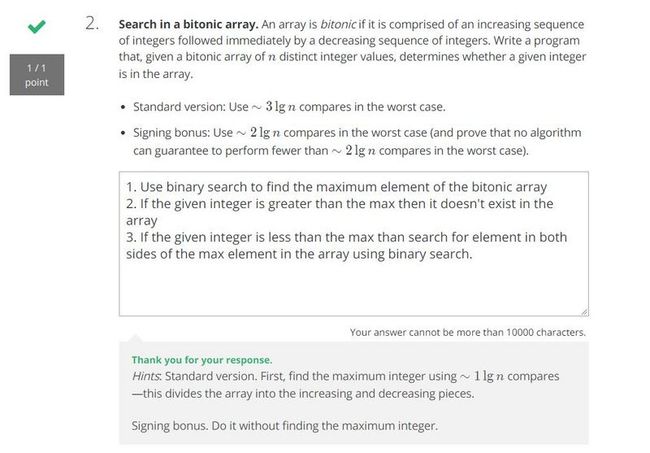
面试问题
- 大意解释待更新...
- 大意解释待更新...
- 大意解释待更新...
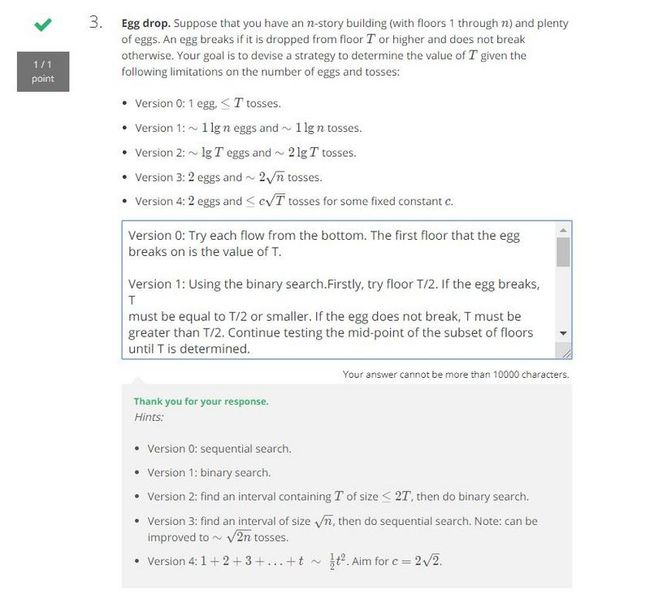
Version 0: Try each flow from the bottom. The first floor that the egg breaks on is the value of T.
Version 1: Using the binary search.Firstly, try floor T/2. If the egg breaks, T must be equal to T/2 or smaller.
If the egg does not break, T must be greater than T/2. Continue testing the mid-point of the subset of floors
until T is determined.
Version 2: Start test at floor 1 and exponentially grow (2^t) floor number (1, 2, 4, 8 ... 2^t)until first egg
breaks. The value of T must be in [2^(t-1), 2^t). This step costs lgT tosses. Then in the range got from last
step can be searched in ~lgT tosses using the binary search. Two step will cost ~2lgT tosses.
Version 3: Test floors in increments of sqrt(N) starting from the first floor.
{e.g: {1, sqrt(N), 2*sqrt(N), 3*sqrt(N)...t*sqrt(N)...}. When the egg breaks on t, test floor from (t-1)*sqrt(N)
and increment by each floor.
The remaining sqrt(N){e.g [(t-1)*sqrt(N), t*sqrt(N))} tests will be enough to check each floor between floor t-1
and t. The floor that breaks will be the value of T.
Version 4: Start test at floor 1 in increments of t^2 (e.g {1,4,9...t^2..N}), When the egg breaks on t, test
floor from (t-1)^2+1 and increment by each floor.