最近和朋友聊TreeMap、HashMap、ConcurrentHashMap的底层原理时,都知道用到了红黑树,但红黑树到底是一个什么样子的算法,我们却并不清楚。
今天简单总结下这个算法的原理,因为网上相关的文章已经很多,本文就不再赘述了。
直接在我觉得讲解的最透彻的文章上做些总结扩展:
红黑树(一)之 原理和算法详细介绍
PS:这篇文章思路和原理是讲的特别清楚的,但遗憾的是,配图是错误的;另外删除节点部分个人觉得讲解的不太清晰。这两个问题导致我思考时走了很大弯路。大家可以以这篇文章为主,参考我的总结来看,可能会好些
1. 红黑树概述
二叉查找树
左节点key < 其根节点key < 右节点key平衡二叉树
平衡二叉树是对 二叉查找树的一种优化,规定左右两个子树的高度差的绝对值不超过1,这样便提高了查找的效率。红黑树
红黑树是 “平衡二叉树” 的一种实现算法。
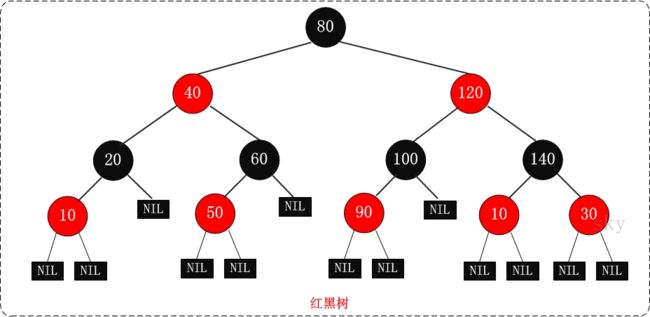
红黑树的特性:
- 每个节点或者是黑色,或者是红色
- 根节点是黑色
- 每个叶子结点(NIL,这里的叶子结点不是传统的叶子结点,是指为空的叶子结点)是黑色。
- 如果一个结点是红色的,则它的子结点必须是黑色的
- 从一个结点到该结点的子孙结点的所有路径上包含相同数目的黑结点。
这些特性一眼看上去好像不知所云。不要急,这里我们只需大致明白:红黑树就是利用红、黑节点接近均匀分布(特性4),而每条路径的黑节点数目一样(特性5)来做到 左右两子树 高度差<=1
2. 算法实现
2.1 左右旋
红黑树左右旋的目的在于,在插入、删除节点后,重新调整红黑节点的位置,使其满足红黑树特性。
-
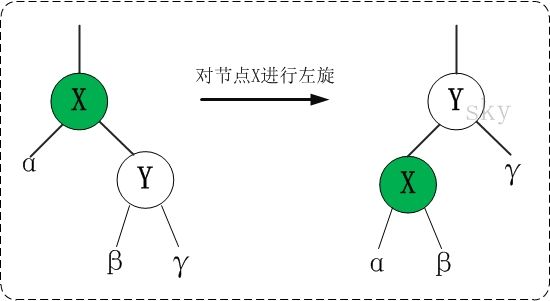
左旋:
将节点绕其右子节点,向左进行旋转,使右子节点变为父节点:
-
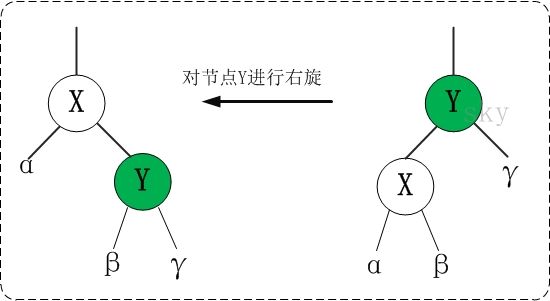
右旋:
将节点绕其左子节点,向右进行旋转,使左子节点变为父节点(注意图的箭头方向是相反的):
2.2 插入
插入分为两步
插入第一步:
将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。注意,节点为红色,这是为了防止父节点为红色,导致违反特性4
/*
* 将结点插入到红黑树中
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的node
*/
private void insert(RBTNode node) {
int cmp;
RBTNode y = null;
RBTNode x = this.mRoot;
// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp < 0)
y.left = node;
else
y.right = node;
} else {
this.mRoot = node;
}
// 2. 设置节点的颜色为红色
node.color = RED;
// 3. 将它重新修正为一颗二叉查找树
insertFixUp(node);
}
插入第二步:
重新调整红黑树,使新插入的节点不破坏红黑树特性:
插入调整分三种情况:
(1. 插入的为根节点,直接节点颜色改为黑色
(2. 被插入的节点的父节点是黑色。不用作改变
(3. 被插入的节点的父节点是红色节点,这种情况最复杂,分场景解决:
这三种场景的处理策略都是为了:将不合规的红色节点移动到根节点,然后将根节点设为黑色。
下面将红黑树(一)之 原理和算法详细介绍中的图修正,来过一遍情况3的三种插入场景:
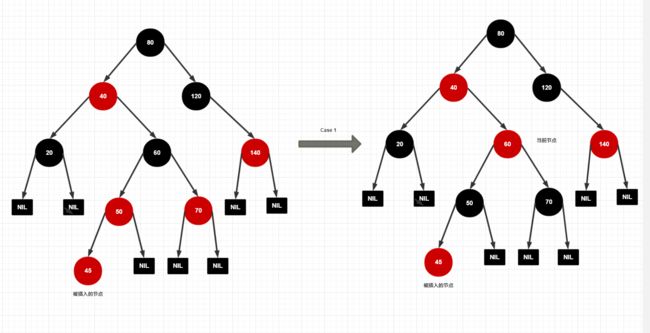
对已存在 [80, 40, 120, 20, 60, 50, 70, 140] 节点的红黑树插入一个 45的节点
-
Case 1:调整的目的为了将红色节点上移,上移后若新的当前节点为根节点,则红黑树合规:
-
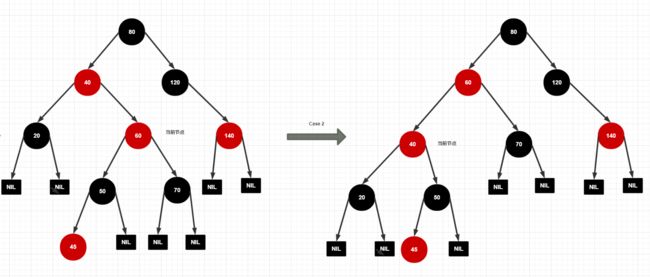
Case 2:将父节点左旋的目的在于,使当前节点的红色上移。上移后若当前节点为根节点,则红黑树合规。牢记我们的处理策略:将不合规的红色节点上移到根节点
上移成功后,再以父节点为当前节点的原因是,从下至上解决不合规问题。
-
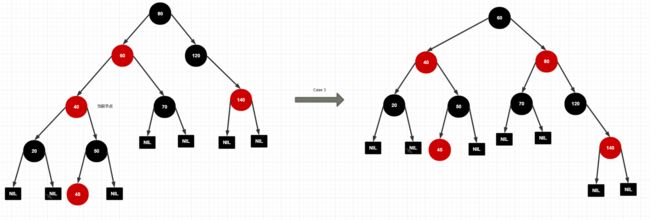
Case 3:这种情况的处理逻辑是,父节点变黑——》分支红色 -1,为补偿令 祖父节点变红 ——》分支红色 +1 。
最后让祖父节点右旋,使得父节点(黑 60)变成了当前节点(红 40)和祖父节点(红 80)的父节点,红黑树合规。
/*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的z
*/
private void insertFixUp(RBTNode node) {
RBTNode parent, gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while (((parent = parentOf(node))!=null) && isRed(parent)) {
gparent = parentOf(parent);
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent.left) {
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.right;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent.right == node) {
RBTNode tmp;
leftRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
} else { //若“z的父节点”是“z的祖父节点的右孩子”
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.left;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent.left == node) {
RBTNode tmp;
rightRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
}
// 将根节点设为黑色
setBlack(this.mRoot);
}
2.3 删除
删除也分为两步
删除第一步:
将红黑树当作一颗二叉查找树,将节点删除:
- 若被删节点 没有子节点,则不做处理;
- 若子节点有一个,则将子节点取代被删除节点;
- 若子节点有2个,则找到后继节点或先驱节点取代该节点。(后继节点即右子树的最小节点,前驱节点为左子树的最大节点)
/*
* 删除结点(node),并返回被删除的结点
*
* 参数说明:
* node 删除的结点
*/
private void remove(RBTNode node) {
RBTNode child, parent;
boolean color;
// 被删除节点的"左右孩子都不为空"的情况。
if ( (node.left!=null) && (node.right!=null) ) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
RBTNode replace = node;
// 获取后继节点
replace = replace.right;
while (replace.left != null)
replace = replace.left;
// "node节点"不是根节点(只有根节点不存在父节点)
if (parentOf(node)!=null) {
if (parentOf(node).left == node)
parentOf(node).left = replace;
else
parentOf(node).right = replace;
} else {
// "node节点"是根节点,更新根节点。
this.mRoot = replace;
}
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace.right;
parent = parentOf(replace);
// 保存"取代节点"的颜色
color = colorOf(replace);
// "被删除节点"是"它的后继节点的父节点"
if (parent == node) {
parent = replace;
} else {
// child不为空
if (child!=null)
setParent(child, parent);
parent.left = child;
replace.right = node.right;
setParent(node.right, replace);
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = null;
return ;
}
if (node.left !=null) {
child = node.left;
} else {
child = node.right;
}
parent = node.parent;
// 保存"取代节点"的颜色
color = node.color;
if (child!=null)
child.parent = parent;
// "node节点"不是根节点
if (parent!=null) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.mRoot = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = null;
}
删除第二步:
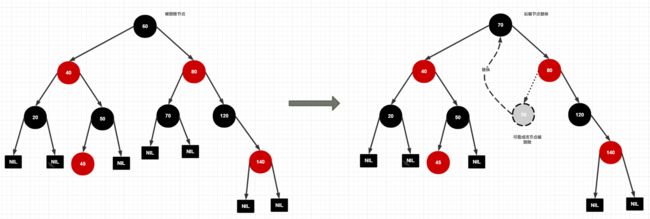
对于 3 的情况,如果用后继节点或前驱节点替换了删除节点,则可视为删除的节点为替换的后继节点或前驱节点。
如下图,原删除节点 60 被后继节点 70 “替换”,可看成 “真实的删除节点” 为 后继节点 70
接下来讨论下删除后继节点的处理:
- 后继节点只会有0个子节点,或一个右子节点。
- 如果被删除的后继节点y为红色,则不会影响到红黑树。若后继节点没有子节点,则不作处理。若有右子节点x,则直接用子节点x替换即可。
- 如果被删除的后继节点y为黑色。若后继节点没有子节点,则不作处理。若有右子节点x,则特性5可能被破坏(该分支少了一个黑色),需要对红黑树进行重新调整,使其不破坏红黑树特性。
调整策略如下:
将被删除的后继节点的黑颜色放到其右子节点x中。即右子节点x 颜色为 “红+黑” 或 “黑+黑” 。然后将x多余的颜色想办法移动到根节点,则红黑树特性不会被破坏。
这种调整策略,又可以概括为3种情况:
① 情况说明:x是“红+黑”节点。
处理方法:直接把x设为黑色,结束。此时红黑树性质全部恢复。
② 情况说明:x是“黑+黑”节点,且x是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。
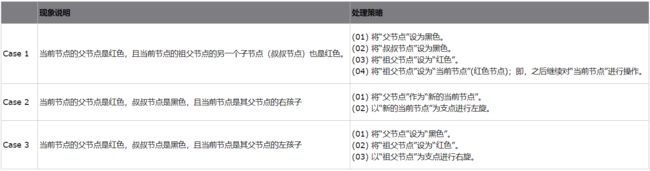
③ 情况说明:x是“黑+黑”节点,且x不是根。
处理方法:这种情况又可以划分为4种子情况。这4种子情况如下表所示:
/*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 待修正的节点
*/
private void removeFixUp(RBTNode node, RBTNode parent) {
RBTNode other;
while ((node==null || isBlack(node)) && (node != this.mRoot)) {
if (parent.left == node) {
other = parent.right;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
leftRotate(parent);
other = parent.right;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.right==null || isBlack(other.right)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.left);
setRed(other);
rightRotate(other);
other = parent.right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.right);
leftRotate(parent);
node = this.mRoot;
break;
}
} else {
other = parent.left;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
rightRotate(parent);
other = parent.left;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.left==null || isBlack(other.left)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.right);
setRed(other);
leftRotate(other);
other = parent.left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.left);
rightRotate(parent);
node = this.mRoot;
break;
}
}
}
if (node!=null)
setBlack(node);
}
3. Java集合中的使用
Java集合中,TreeMap和TreeSet都是有序的,它们其实就是用红黑树实现。
另外,HashMap和ConcurrentHashMap也使用了红黑树结构进行优化,当hash冲突的链表个数达到8时,为了查询优化,会将链表改为红黑树