软件测试实习0705-正交表

正交表是一整套规则的设计表格，用 L为正交表的代号，n为试验的次数，t为水平数，c为列数，也就是可能安排最多的因素个数。正交表的构造需要用到组合数学和概率学知识，现在广泛使用的L_n（t^c）类型的正交表构造思想比较成熟。

基本介绍

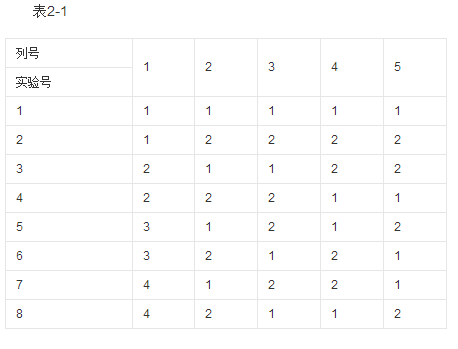
正交表例如L₉（3⁴），表1-1， 它表示需作9次实验，最多可观察4个因素，每个因素均为3水平。一个正交表中也可以各列的水平数不相等，我们称它为混合型正交表，如L₈（4¹×2⁴），表2-1 ，此表的5列中，有1列为4水平，4列为2水平。根据正交表的数据结构看出，正交表是一个n行c列的表，其中第j列由数码1，2，… Sj 组成，这些数码均各出现N/S次，例如表1-1中，第二列的数码个数为3，S=3 ，即由1、2、3组成，各数码均出现3次。

主要性质

1.正交表具有以下两项性质：

⑴每一列中，不同的数字出现的次数相等。例如在两水平正交表中，任何一列都有数码“1”与“2”，且任何一列中它们出现的次数是相等的；如在三水平正交表中，任何一列都有“1”、“2”、“3”，且在任一列的出现数均相等。

⑵任意两列中数字的排列方式齐全而且均衡。例如在两水平正交表中，任何两列（同一横行内）有序对子共有4种：（1，1）、（1，2）、（2，1）、（2，2）。每种对数出现次数相等。在三水平情况下，任何两列（同一横行内）有序对共有9种，1.1、1.2、1.3、2.1、2.2、2.3、3.1、3.2、3.3，且每对出现数也均相等。

以上两点充分的体现了正交表的两大优越性，即“均匀分散性，整齐可比”。通俗的说，每个因素的每个水平与另一个因素各水平各碰一次，这就是正交性。这个特点保证了试验点均匀地分散在因素与水平的完全组合之中，因此具有很强的代表性。

 

Orthogonal Array TestingStrategy，正交表测试策略

•    OATS的好处

•    1，可以组合所有的变量；

•    2，得到一个最小的测试集，这个集合，包括最少的测试用例，并且，包括了所有变量的组合,

•    3，得到的变量的组合是均匀的分布的（这一点可以参照上面的正交表的特点）；

•    4，可以测试用一些复杂的组合；

•    5，它的，不像手工测试那生成的测试用例是有迹可循日，即有规律样会遗漏一些用例的组合。

•    选择OATS的基本原则

•    （1）先看水平数。

•    (2)要看测试精度的要求。若要求高，则宜取测试次数多的正交表。

•    (3)不宜选实验次数太多的正交表

•    (4)按原来考虑的因素、水平和交互作用去选择正交表，若无正好适用的正交表可选，简便且可行的办法是适当修改原定的水平数。

•    (5)在核心功能上选择结果集合较多的正交表

 

具体步骤：

1，先要知道你有多少个变量？它对应到正交表的概念中的因素数。

2，查看每个变量的测试取值个数（这里我用a代替，以方便后面调用），这个取值不是说这个变量的取值范围中包括多少个值，而是用等价类划分出来的（边界值等方法也在这里应用到）。

3，选择正交表，我们选择正交表时，要满足两点：因素数（即变量个数）和水平数。在选择正交表的时候，要保存：

A、正交表的列不能小于变量的个数；

B、正交表的水平数不能小于a。

4，拿着自己的因素数和水平数，去找对应的正交表，按3中说的原则，现在正交表有一部分已经在网上公布了，在很大程度上已经够设计测试用例用了，如果你的情况太特殊，也可以考虑自己去推算。

5，如果你选择的正交表中某个因素数有剩余的水平数，就拿这个因素数的值从上到下循环代进去。以增加发现缺陷的机会。

6，按次数设计用例，每次数对应一个用例。设计完成后，如果觉得有些组合是可能会有问题的，而正交表中又没有包括，那就增加一些用例。