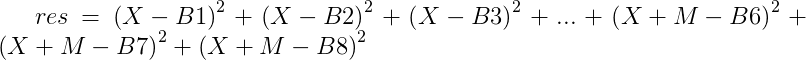西北大学2019校赛题解(补题,非官方)

（蒟蒻题解）.

所有题目的链接:https://www.cometoj.com/contest/33

然后给出出题大佬的博客QWQ:https://blog.csdn.net/qq_41643650

A:小姐姐分发气球，小姐姐越多，那么限制条件下完成发气球的任务就会成功，很容易想到二分小姐姐的数量。

那么我们用优先队列模拟送气球的过程，总时间复杂度O(n*log(n)*log(n));

#include
#include
#include
#include
#include
#include
using namespace std;

const double epos=1.0e-7;
const int inf=0x3f3f3f3f;
typedef long long ll;

priority_queue,greater >q;

const int maxn=2e5+7;
struct Node{
	ll t;
	int id;
	bool operator <(const Node& x)const{
		if(t!=x.t) return t=d) return 0;
			q.pop();
			q.push(tt+t);
		}
	}
	return 1;
}

int main(){
	scanf("%d%d%d%d",&n,&m,&t,&d);
	
	for(int i=0;i>1;
		if(check(mid))
			r=mid-1;
		else
			l=mid+1;
	}
	printf("%d\n",l);
	return 0;
}

 

B:求房子高度。三分。

我们设当前所有房子中最低的高度是x,那么允许出现的最高高度就是x+m了,于是将所有比x低的高度都修改为x,比x+m高的修改为x+m,处于[x,x+m]的则无需修改.

展开这个式子，发现是一个开口向上的二次函数,其中X为自变量,其余都是已知,满足先减后增的性质,故可用三分求极值.

这里我们先将B数列排序，再预处理他的前缀和与前缀平方和，那么O(log*log)足够了。(第二个log为每次找比X小的数，比X+M大的数)

 

#include
#include
#include
#include
#include

using namespace std;
typedef long long ll;
const int maxn=2e5+7;
const ll inff=0x3f3f3f3f3f3f3f3f;
int a[maxn];
int n,m;

ll sum[maxn];
ll mul[maxn];

ll res;



int myfind(int h){//最后一个小于h的数的下标; 
	int l=1,r=n,mid;
	while(l<=r){
		mid=(l+r)>>1;
		if(a[mid]>=h) r=mid-1;
		else l=mid+1;
	}
	return r;
}

int myfind1(int h){//第一个大于h的数的下标; 
	int l=1,r=n,mid;
	while(l<=r){
		mid=(l+r)>>1;
		if(a[mid]<=h) l=mid+1;
		else r=mid-1;
	}
	return l;
}

/*
h为此次查询中，允许出现的最低的房子高度，则h+m为最大的允许高度，
那么高度在[h,h+m]内的房子不用改变高度 
*/

ll check(int h){
	int l=myfind(h);
	int r=myfind1(h+m);
	ll tmp=0;
	tmp+=mul[l]+h*1LL*h*l-2LL*h*sum[l];
	if(r<=n)
		tmp+=mul[n]-mul[r-1]+(h+m)*1LL*(h+m)*(n-r+1)-2LL*(h+m)*(sum[n]-sum[r-1]);
	return tmp;
	
	
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		scanf("%d",&a[i]);
	sort(a+1,a+n+1);
	for(int i=1;i<=n;++i){
		sum[i]=sum[i-1]+a[i];
		mul[i]=mul[i-1]+a[i]*1LL*a[i];
	}
	
	int l=1,r=a[n]+m,mid,midr;
	while(l>1;
		midr=(mid+r)>>1;
		if(check(mid)<=check(midr))
			r=midr;
		else
			l=mid;
	}
	printf("%lld\n",min(check(l),check(r)));
}

 

G: 最短路

该题注意使用邻接表存储时，开大一点，否则RE。还有就是nlogn的时间预处理所有数的因子。

 

假设当前房间为i号，它的四个属性值: a[i],b[i],c[i],d[i]; 那么从i->d[i]会花费a[i]+a[d[i]]元,也可以选择去k+i号房间(c[i[%k==0) 花费b[i]+a[i]+a[d[i]]元，于是我们建个图，跑最短路就行。 注意题目要求从1跑到n,如果我们每次加边的时候都把当前房间的a[i]加到路径中的话,(比如三个点a,b,c,用v[]表示过路费, 从a->b加边时加上了两间房子的过路费,b->c的边也加了b,c的过路费,那么最后算出来的最短路就会是v[a]+v[b]+v[b]+v[c])会出现一条路径上重复多次计算一个房间的花费,所以我们建图的时候不加当前房间的a[i],最后算出dis[n]的时候加上a[1]即可。

迪杰斯特拉堆优化或者spfa都可。

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f3f3f3f3f;

const int maxn=2e5+7;
ll dis[maxn];
bool vis[maxn];

int head[maxn];
int top;
struct Edge{
	int v,next;
	ll w;
}edge[20000009];

void init(){
	memset(head,-1,sizeof(head));
	top=0;
}
void add(int u,int v,ll w){
	edge[top].v=v;
	edge[top].w=w;
	edge[top].next=head[u];
	head[u]=top++;
}
int n;
ll a[maxn],b[maxn],c[maxn],d[maxn];

priority_queue< pair >q;

void dij(){
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[1]=0;
	q.push(make_pair(0,1));
	int u,v;
	ll w;
	while(!q.empty()){
		u=q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=head[u];i!=-1;i=edge[i].next){
			v=edge[i].v;
			w=edge[i].w;
			if(dis[v]>dis[u]+w){
				dis[v]=dis[u]+w;
				q.push(make_pair(-dis[v],v));//负权边存入相当于小顶堆,权值大的化为负后就变小了,自然就在堆底; 
			}
		}
	}
	if(dis[n]==inf) printf("-1\n");
	else printf("%lld\n",dis[n]+a[1]);
	
}
vectorv[maxn];

int main(){
	for(int i=1;in) break;
			add(i,i+h,b[i]+a[i+h]);
		}
	}
	dij();
	
	return 0;
}