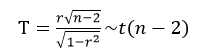【R语言】读懂Pearson相关分析结果
1.数据说明
这里我对R语言的自带的数据包中states.x77(关于美国50个州的某些数据)第1至6列的50份数据从统计的角度以及R语言的角度进行分析,看看R语言是怎么做相关分析的,同时怎么看分析出的结果
首先我们观察一下states.x77中第1至6列的数据及其意义
| 列名 | 解释 | 单位 |
|---|---|---|
| Population | 人口 | 人 |
| Income | 人均收入 | 美元/人 |
| Illiteracy | 文盲率 | % |
| Life Exp | 预期寿命 | 年 |
| Murder | 谋杀率 | %(每100,000人) |
| HS Grad | 高中毕业率 | % |
2.统计学的计算过程
(1)我们拿出文盲率(设为x)和预期寿命(设为y)来从统计的角度计算相关系数r以及显著性水平α:
首先,我们假设文盲率和预期寿命符合计算Pearson相关系数的变量要求:
①两变量相互独立
②两变量为连续变量
③两变量的分布遵循正态分布
④两变量呈线性关系
换句话来说,当你选择的变量符合上要求的时候,可以选择使用Pearson相关系数来求两个变量间的相关关系
(2)按照上一篇文章对相关分析的解说,计算Pearson相关系数的时候,有两个步骤:
①计算相关系数r
②计算显著性水平α
因此这里作出简单的讲解:
①计算相关系数r
Pearson的相关系数r的公式为:
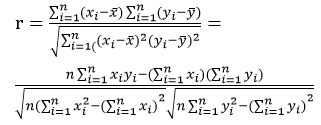
那么把数据代入到公式中计算
#state.x77第3列为文盲率
x <- state.x77[,3]
#state.x77第4列为预期寿命
y <- state.x77[,4]
#样本总数为50
n <- nrow(state.x77)
#按照公式设置分子
Numerator <- (n*sum(x*y)-sum(x)*sum(y))
#按照公式设置分母
Denominator <- (sqrt(n*sum(x^2)-sum(x)^2)*sqrt(n*sum(y^2)-sum(y)^2))
#计算出相关系数r
r <- Numerator / Denominator
r
[1] -0.5884779这个时候我们根据1977年发布的美国50个州的states.x77样本中的数据算出了相关系数r=-0.5884779,因为样本states.x77只是从总体(设为总体A)抽出来的数据(总体应该是这么多年来美国各个州的文盲率和预期寿命的数据),那么这个states.77样本中算出的相关系数r并不一定能代表总体A的相关系数ρ
②计算显著性水平α
设想一下,如果我们的总体A的相关系数ρ实际上为0的(也就是说总体上文盲率和预期寿命没有相关关系),因为误差或者抽样偏差的关系,抽样所得的states.x77的文盲率和预期寿命数据计算出来的相关系数r并不为0(也就是说样本上显示文盲率和预期寿命有相关关系),因此要进行显著性检验:
提出假设:
H0:总体A的相关系数ρ=0(也就是说假设总体上文盲率和预期寿命没有相关关系)
H1:总体A的相关系数ρ≠0(也就是说总体上文盲率和预期寿命有相关关系)
把数据代入公式中计算:
T <- r*(sqrt(n-2))/sqrt(1-r^2)
T
[1] -5.042706得出T=-5.042706
3.R语言应用以及观察结果
在R语言中,有直接的函数cor( )计算出Pearson相关系数
同样是两个步骤:
计算文盲率和预期寿命之间的相关系数r:
r <- cor(state.x77[,3],state.x77[,4])
r
[1] -0.5884779和我们使用计算Pearson系数计算出的结果一致
进行显著性检验
#使用cor.test()函数计算文盲率和预期寿命的相关关系,默认方法为Pearson相关分析
T <- cor.test(state.x77[,3],state.x77[,4])
T
Pearson's product-moment correlation
#这里列名数据来源
data: state.x77[, 3] and state.x77[, 4]
#t值和使用显著性检验的公式计算出的t值一致
#自由度df为n-2=48
#p值查表可以得出6.969e-06 < 0.05
t = -5.0427, df = 48, p-value = 6.969e-06
#因此有95%以上的几率可以拒绝原假设总体A的相关系数ρ=0
#即文盲率和预期寿命的相关系数显著地不为0
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.7448226 -0.3708811
#这里列示Pearson相关系数
sample estimates:
cor
-0.58847794.R语言扩展应用
当我们不仅仅需要计算文盲率和预期寿命的相关关系,而是计算state.x77中各个数据之间的相关关系,使用cor()也是可以做到的:
再次按照相关分析的步骤:
①计算相关系数r(两两变量间的相关系数)
> cor(state.x77[1:6)
Population Income Illiteracy Life Exp
Population 1.00000000 0.2082276 0.10762237 -0.06805195
Income 0.20822756 1.0000000 -0.43707519 0.34025534
Illiteracy 0.10762237 -0.4370752 1.00000000 -0.58847793
Life Exp -0.06805195 0.3402553 -0.58847793 1.00000000
Murder 0.34364275 -0.2300776 0.70297520 -0.78084575
HS Grad -0.09848975 0.6199323 -0.65718861 0.58221620
Frost -0.33215245 0.2262822 -0.67194697 0.26206801
Area 0.02254384 0.3633154 0.07726113 -0.10733194
Murder HS Grad
0.3436428 -0.09848975
-0.2300776 0.61993232
0.7029752 -0.65718861
-0.7808458 0.58221620
1.0000000 -0.48797102
-0.4879710 1.00000000
-0.5388834 0.36677970
0.2283902 0.33354187②计算显著性水平α
> #赋值state.x77中第1至6列的数据给states
> states <- state.x77[,1:6]
> #执行对states中的缺失值进行行删除的显著性检验
> corr.test(states, adjust = "none", use = "complete")
Call:corr.test(x = states, use = "complete", adjust = "none")
Correlation matrix
#进行Pearson相关系数计算
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00 0.21 0.11 -0.07 0.34 -0.10
Income 0.21 1.00 -0.44 0.34 -0.23 0.62
Illiteracy 0.11 -0.44 1.00 -0.59 0.70 -0.66
Life Exp -0.07 0.34 -0.59 1.00 -0.78 0.58
Murder 0.34 -0.23 0.70 -0.78 1.00 -0.49
HS Grad -0.10 0.62 -0.66 0.58 -0.49 1.00
#样本数
Sample Size
[1] 50
#进行显著性检验
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Population Income Illiteracy Life Exp Murder HS Grad
Population 0.00 0.15 0.46 0.64 0.01 0.5
Income 0.15 0.00 0.00 0.02 0.11 0.0
Illiteracy 0.46 0.00 0.00 0.00 0.00 0.0
Life Exp 0.64 0.02 0.00 0.00 0.00 0.0
Murder 0.01 0.11 0.00 0.00 0.00 0.0
HS Grad 0.50 0.00 0.00 0.00 0.00 0.0
To see confidence intervals of the correlations, print with the short=FALSE option
从以上结果可以看出,具有显著性相关关系(设显著性水平为0.05,即超过95%的概率有相关关系)的两两变量有:
| 变量 | P值 | r值 |
|---|---|---|
| Population,Murder | 0.01 | 0.34 |
| Income, Illiteracy | 0.00 | -0.44 |
| Income,Life Exp | 0.02 | 0.34 |
| Income, HS Grad | 0.00 | 0.62 |
| Illiteracy, Life Exp | 0.00 | -0.59 |
| Illiteracy, Murder | 0.00 | 0.70 |
| Illiteracy, HS Grad | 0.00 | -0.66 |
| Life Exp, HS Grad | 0.00 | 0.58 |
| Life Exp, Murder | 0.00 | -0.78 |
| Murder, HS Grad | 0.00 | -0.49 |