Learning to Rank 的实践

1 背景介绍

排序问题（Ranking）是信息检索领域的核心问题，如文档索引，协同过滤等。Learning to rank（LTR） 也叫 Machine-learned ranking，指的就是用机器学习的方法来解决文档排序问题 ¹。Learning to rank 的思想就是建立一个模型 LTR，当我们输入某个查询 q 时，能够从文档及 D 中找出相关的文档并排序，LTR 模型大体框架如下图所示。

因此熟悉机器学习的人都知道那老一套，用训练集训练出 LTR 模型，然后对于查询作预测，这样一来排序问题就变成了预测问题。假设我们有大量的文档，也有大量的查询，也有查询和文档之间的相关联系，那么我们就可以构造一个基本的训练集。

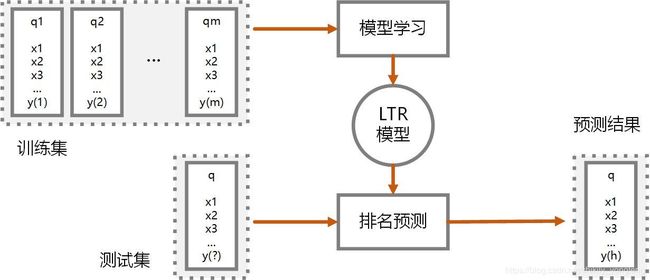
在这个训练集中，每一条训练数据其实就是一个查询文档对（query-document pair，即查询（query）和文档（document））及其相关度（relevance degree）。其中，文档 当然是以特征的形式来记录，可类比于空间向量模型或者词袋模型；查询 则以数值形式来记录；这里的 相关系数 则有不同的记录方式，主要有 3 种，

• Relevance degree：用相关度来数数值化相关关系。比如用数字 [1,2,3,4,5] 分别表示相关程度 Perfect，Excellent，Good，Fair，Bad。再比如用数字 [0,1] 分别表示 relevant 和 irrelevant。
• Relevance preference：用 2 个文档的相对关系来表示相关关系。如在查询 q1 时，文档 A 比文档 B 更相关，我们记录为 A $>$ B。
• Total order：用某个查询下的文档排列顺序作为我们的相关关系。如在查询 q1 下，排序为 A，B，C，…。这个排序关系本身就可以提供 Relevance degree 和 Relevance preference 的信息。

2 方法介绍

Learning to rank 的方法浩如烟海，现有的分类标准主要来自微软亚洲研究院的 Tie-Yan Liu 研究员的论文 Learning to Rank for Information Retrieval ²，Liu 博士按照这些方法的输入形式（input presentation）和损失函数（loss function）将这些方法划分为：Pointwise，Pairwise，和 Listwise 方法。在 Dandekar 的博客 ³ 中也对这三种方法进行了介绍，这三种方法的区别就在于训练模型时，一次要考虑多少个文档。

At a high level, Pointwise, Pairwise and Listwise approaches differ in how many documents you consider at a time in your loss function when training your model.
— Nikhil Dandekar

不过，后续 Niek Tax 在论文 A Cross-Benchmark Comparison of 87 Learning to Rank Methods ⁴ 中研究证明 Listwise 要优于前两种方法的。这里简单概述一下上述三种方法。

2.1 Pointwise

Pointwise 方法通过计算单个文档的相关性来建立 LTR 模型。由于训练集中的每个查询文档对都有对应的一个相关度（看作是一个数值），因此在训练集上得到的模型，可以直接用来预测新来的查询文档对的相关度。这种方法属于有监督的方法。

在给每个文档打标记的时候，我们可以直接标上“相关 - 不相关”的标记，也可以按照等级标记为 “不相关 - 弱相关 - 相关 - 很相关 - 强相关”，这个时候排序问题转化为了二 / 多分类问题。另外，我们也可以按照相关度标记上数值，如“0，1，2，…” 等，这个时候排序问题转化为了回归问题。

训练集可以标记为如 (a) 所示，其中 $q$ 为查询，$x_1$ 到 $x_m$ 为相关文档的排名。训练集中的每个实例为文档及其相关系数，这个系数可以是类别也可以是数值，如 ($x_1$, $y_1$) 表示文档 $x_1$ 的相关系数为 $y_1$。

该类算法包括 Pranking，OAP-BPM 和 McRank 等。

2.2 Pairwise

Pairwise 方法通过比较相邻的文档的相关性来建立 LTR 模型。由于训练集中的任意 2 条查询文档对总会有一个相对大小的关系，因此根据训练集中的文档对的大小关系条件训练出分类模型，然后预测新查询下的各个文档之间的大小关系，进而对各个文档进行排序。

训练集可以标记为如 (b) 所示，其中 $q$ 为查询，$x_1$ 到 $x_m$ 为相关文档的排名。训练集的每个实例均为两个文档之间的相关性，如 ($x_1$, $x_2$, +1) 表示 $x_1$ 比 $x_2$ 更相关，($x_m$, $x_2$, -1) 表示 $x_2$ 比 $x_2$ 更相关。

该类算法包括 RankBoost, RankNet 和 Ranking SVM 等。

2.3 Listwise

Listwise 方法将文档在整体数据集中的排名来建立 LTR 模型。也就是说 Listwise 方法考虑整个文档，而不是单个文档或者文档对。这类算法比较复杂，本文暂时缺省。

该类算法主要包括 AdaRank、SVM-MAP、ListNet 和 SoftRank 等。

3. 评价标准

模型的好坏总有一套度量标准，LTR 模型的评价标准主要有 MAP 和 NDCG 等。本文着重介绍前者。MAP 全称 Mean of Average Precision（平均精确度的均值），它反映了查询结果中前 k 名的相关性。首先，我们可以计算查询 $q_i$ 的精确度 $P@K$ 如下，

$$P@K=\frac{\#\{Relevancedocumentsintopkresults\}}{k}$$

然后，我们可以进一步计算查询 $q_i$ 的 Average of Precision （AP）如下，假设 $q_i$ 有 n 个返回结果，那么对应的 $A{P}_i$ 为，

$$A{P}_i=\frac{{\sum }_{k=1}^{n}P@K\times I_k}{\#\{Relevancedocuments\}}$$

最终，我们可以求得 MAP 如下，对于所有的 m 个 查询求他们的 AP 值得平均值。

$$MAP=\frac{1}{m}(\sum _{i=1}^{m}A{P}_i)$$

例如，对于查询 $q_1$ 的预测排名前 5 分别是 “相关，不相关，相关，不相关，相关” （其中绿色表示相关，红色表示不相关），那么根据 MAP 的计算公式，我们计算得出模型在前 5 名的 AP 为，

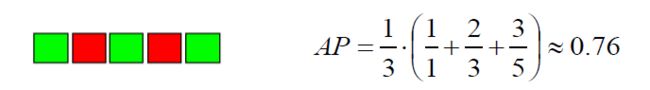
最后，我们求取 $q_1$ 到 $q_i$ 的预测结果 AP 的平均值，就可以得到 MAP 的值。

【注】LTR 模型有许多常见的评价标准，包括 NDCG 等，本文不一一展开介绍，详细请查看文献 ² 。

4. Ranklib 实践

Ranklib 是一个开源项目，其中包含了绝大多数学术界中的 LTR 方法。我们可以直接在其官网 ⁵ 下载 jar 包，由于这个包是可执行的 jar 包，因此下载后直接在控制台运行即可。

4.1 显示参数

首先，在控制台输入 -jar 会显示 Ranklib 的所有参数，如 -train 表示训练数据的路径，-ranker 表示使用排序算法的类别，-save 表示模型保存的路径等。

> java -jar RankLib-2.1-patched.jar

4.2 选用算法

接着，我们指定学习算法（-ranker），输入训练集（-train），将学习到的 LRT 模型存放（-save）到文件中去，这里其实也可以添加上 -validation 可选参数用来降低模型的过拟合。

> java -jar RankLib.jar -train train.txt -ranker 6 -save mymodel.txt

其中， -ranker 参数有 10 种方法可选，其中 6 表示 LambdaMART 算法，而 LambdaMART 算法又拥有自己的独有参数，如 -tree 表示生成树的个数，-leaf 表示每棵树上的叶子结点个数，-tc 树的划分阈值等。我们可以进一步补充参数如下，

> java -jar RankLib.jar -train train.txt -ranker 6 -tree 1000 -leaf 10 
       -tc 256 -save mymodel.txt

Ranklib 的训练集是一个格式化的 txt 文件，每一条数据从左往右依次表示：相关度，查询 id，特征列表，注释，即 qid: : ... # ，注意 # 号后面的注释信息对于建模没有任何影响，Ranklib 会自动忽略掉。

4.3 模型训练

下面是一个简单的训练集 train.txt，它的内容有 8 行，其中在 qid 为 1 时，文档 1A，1B，1C，1D 的相关度分别是 3，2，1，1，即文档 1A 相关度最高；当 qid 为 2 时，文档 2A，2B 的相关度分别为 1，2，即文档 2B 相关度最高。

// train.txt
3 qid:1 1:1 2:1 3:0 4:0.2 5:0 # 1A
2 qid:1 1:0 2:0 3:1 4:0.1 5:1 # 1B 
1 qid:1 1:0 2:1 3:0 4:0.4 5:0 # 1C
1 qid:1 1:0 2:0 3:1 4:0.3 5:0 # 1D  
1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2A  
2 qid:2 1:1 2:0 3:1 4:0.4 5:0 # 2B 
1 qid:2 1:0 2:0 3:1 4:0.1 5:0 # 2C 
1 qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2D  

我们打开 mymodel.txt 来看一下通过 LambdaMART 算法训练得到的模型，文件中保存了训练得到的 1000 棵树的详细信息。

// mymodel.txt
## LambdaMART
## No. of trees = 1000
## No. of leaves = 10
## No. of threshold candidates = 256
## Learning rate = 0.1
## Stop early = 100
<ensemble>
	<tree id="1" weight="0.1">
		<split>
			<feature> 1 </feature>
			<threshold> 0.0 </threshold>
			...
	</tree>
	<!-- 此处省去另外 999 棵树 -->
</ensemble>

有了这个模型之后，我们既可以据此对新的查询 $q$ 进行文档排序，也可以直接对文档进行排序，也可以进行模型的比较等，具体做法如下，

4.4 样本排序

利用训练好的模型 mymodel.txt 对文件对 myResultList.txt 进行排序，并将得到的结果保存在 myNewResultList.txt 里。

> java -jar RankLib.jar -rank myResultList.txt -load mymodel 
       -indri myNewResultList.txt

在 myNewResultList.txt 中，第一列表示查询 id 号，第二列无明显含义，第三列表示文档 id 号，第四列表示排名，第五列表示预测相关性。有图可见，预测结果基本与原数据集相符。

// myNewResultList.txt
1 Q0 1A 1 100.4518 indri
1 Q0 1B 2 -0.70749 indri
1 Q0 1C 3 -100.28999 indri
1 Q0 1D 4 -100.64357 indri
2 Q0 2B 1 51.78342 indri
2 Q0 2A 2 -50.78343 indri
2 Q0 2D 3 -50.78343 indri
2 Q0 2C 4 -50.88343 indri

4.5 测试集预测

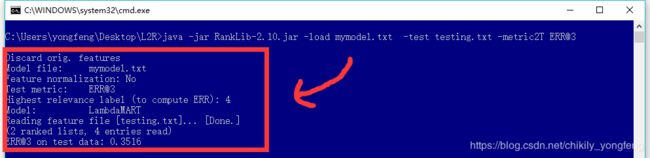
为了测试训练好的模型的预测能力，我们用 mymodel.txt 来对测试集 test.txt 做预测。其中 -metric2T 规定了在测试集上使用的评估标准，另外可选用的参数包括 MAP, NDCG@k, DCG@k, P@k, RR@k 等，

> java -jar RankLib.jar -load mymodel.txt -test test.txt -metric2T ERR@10 

// test.txt
1 qid:1 1:0 2:1 3:0 4:0.4 5:1 # 1H
2 qid:1 1:1 2:0 3:1 4:0.3 5:0 # 1K  
3 qid:2 1:1 2:1 3:1 4:0.2 5:0 # 2F  
2 qid:2 1:1 2:0 3:1 4:0.4 5:1 # 2G 

预测的结果可能是如下形式，可以看出得到的结果是 0.3516。这就是 Ranklib 最常见的一些用法，更多的特征可以进官网 ⁵ 去探索。

---

1. Wikipedia. “Learning to rank.” https://en.wikipedia.org/wiki/Learning_to_rank ↩︎

2. Liu, Tie Yan. “Learning to Rank for Information Retrieval.” Acm Sigir Forum 41.2(2007):58-62. ↩︎ ↩︎

3. Nikhil Dandekar. “Pointwise vs. Pairwise vs. Listwise Learning to Rank”. https://medium.com/@nikhilbd/pointwise-vs-pairwise-vs-listwise-learning-to-rank-80a8fe8fadfd ↩︎

4. Tax, Niek, S. Bockting, and D. Hiemstra. “A Cross-Benchmark Comparison of 87 Learning to Rank Methods.” Information Processing & Management 51.6(2015):757-772. ↩︎

5. Ranklib. https://sourceforge.net/p/lemur/wiki/RankLib/ ↩︎ ↩︎