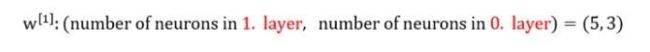全文共5234字,预计学习时长10分钟
图片来源:unsplash.com/@alinnnaaaa
本文将介绍如何建立进阶神经网络。
输入数据
本教程唯一使用的数据库为NumPy。
import numpy as np
激活函数
在隐藏层中会使用tanh激活函数,而在输出层中则会使用sigmod函数。在两种函数的图中都很容易找到信息。下面直接执行函数。
以上为Sigmoid函数。以下为该函数代码:
def sigmoid(x): return (1 / (1 + np.exp(-x)))
设定参数
什么是参数和超参数?参数指权值和偏差。超参数会影响参数,并设置在学习过程开始之前。准确无误设置超参数并不容易,需要不断调整数值。超参数包括学习率、迭代次数、校准率等。
想知道如何设置矩阵规模吗?看看下面的答案吧!
这是什么意思呢?例如:
(第0层,即L=0),输入层神经元数量=3
(第1层,即L=1),隐藏层神经元数量=5
(第2层,即L=2),输出层神经元数量=1
希望以上代码都能奏效!现在设置参数。
def setParameters(X, Y, hidden_size):
np.random.seed(3)
input_size = X.shape[0] # number of neurons in input layer
output_size = Y.shape[0] # number of neurons in output layer.
W1 = np.random.randn(hidden_size, input_size)*np.sqrt(2/input_size)
b1 = np.zeros((hidden_size, 1))
W2 = np.random.randn(output_size, hidden_size)*np.sqrt(2/hidden_size)
b2 = np.zeros((output_size, 1))
return {'W1': W1, 'W2': W2, 'b1': b1, 'b2': b2}
定义变量W1、b1、W2和b2。变量初始值设为0也无妨。但初始化权值时要格外谨慎。初始值绝不能为0。为什么?若权值初始值为0,函数Z = Wx + b的值恒为0。多层神经网络中,每层的神经元共同作用。所以应该如何设置初始权值呢?本文使用he初始化。
公式
# Python implementation np.random.randn(output_size, hidden_size)*np.sqrt(2/hidden_size)
除he初始化以外,也可以使用以下方法:
np.random.randn(output_size, hidden_size)*0.01
建议:在参数初始化中,请勿将权值设为0或大数值。
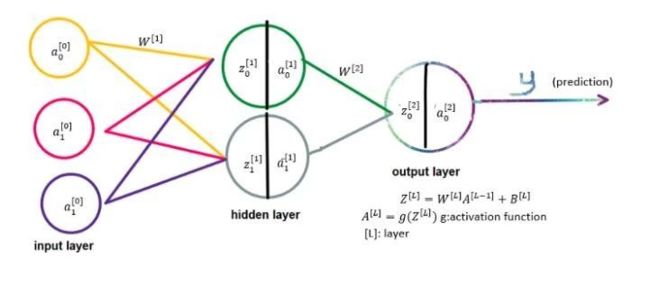
前向传播
前向传播
上图清晰解释了前向传播。在Python中的应用为:
def forwardPropagation(X, params):
Z1 = np.dot(params['W1'], X)+params['b1']
A1 = np.tanh(Z1)
Z2 = np.dot(params['W2'], A1)+params['b2']
y = sigmoid(Z2)
return y, {'Z1': Z1, 'Z2': Z2, 'A1': A1, 'y': y}
为什么要储存 {‘Z1’: Z1, ‘Z2’: Z2, ‘A1’: A1, ‘y’: y}?因为在反向传播中会用到这些数值。
成本函数
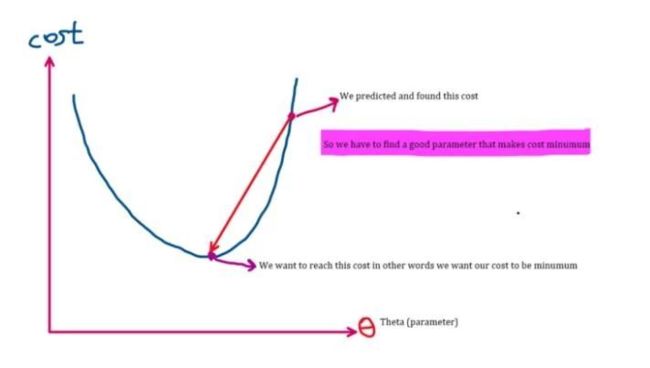
刚才介绍了前向传播,得到预测值(y)。这个值由成本函数计算得出。下图可以说明:
更新参数
更新参数后找到可能最小化成本的最佳参数,本文不会对此再做探讨。但在上一段提到,如果数值在抛物线右侧,导数(斜率)为正,数值递减,左移接近最小成本值;若数值在抛物线左侧,斜率为负,因此参数会增至预期的最小成本值。
以下为使用的成本函数:
成本函数
此成本函数的Python代码:
def cost(predict, actual): m = actual.shape[1] cost__ = -np.sum(np.multiply(np.log(predict), actual) + np.multiply((1 - actual), np.log(1 - predict)))/m return np.squeeze(cost__)
反向传播
确定成本后,下面返回去求权值和偏差的导数。
def backPropagation(X, Y, params, cache):
m = X.shape[1]
dy = cache['y'] - Y dW2 = (1 / m) * np.dot(dy, np.transpose(cache['A1']))
db2 = (1 / m) * np.sum(dy, axis=1, keepdims=True)
dZ1 = np.dot(np.transpose(params['W2']), dy) * (1-np.power(cache['A1'], 2))
dW1 = (1 / m) * np.dot(dZ1, np.transpose(X))
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
return {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}
def backPropagation(X, Y, params,cache)中的parama和cache是什么?在前向传播中储存数值,就是为了用于反向传播。Params是参数(权值和偏差)。
更新参数
得到参数后,代入以下公式:
公式中alpha (α)是超参数的学习率。在学习开始前需要设置数值。在学习率右侧的数值为导数。alpha和导数已知,可以更新参数。
def updateParameters(gradients, params, learning_rate = 1.2):
W1 = params['W1'] - learning_rate * gradients['dW1']
b1 = params['b1'] - learning_rate * gradients['db1']
W2 = params['W2'] - learning_rate * gradients['dW2']
b2 = params['b2'] - learning_rate * gradients['db2']
return {'W1': W1, 'W2': W2, 'b1': b1, 'b2': b2}
循环是关键
需要多次迭代才能找到回归最低成本的参数。现在开始循环!
def fit(X, Y, learning_rate, hidden_size, number_of_iterations = 5000): params = setParameters(X, Y, hidden_size) cost_ = [] for j in range(number_of_iterations): y, cache = forwardPropagation(X, params) costit = cost(y, Y) gradients = backPropagation(X, Y, params, cache) params = updateParameters(gradients, params, learning_rate) cost_.append(costit) return params, cost_
Hidden_size指隐藏层中神经元数量。由于在学习开始前设定,它类似于超参数。return params, cost_指找到的最佳参数。cost_为每次迭代预估的成本。
运行代码!
使用sklearn创建数据集。
import sklearn.datasets X, Y = sklearn.datasets.make_moons(n_samples=500, noise=.2)X, Y = X.T, Y.reshape(1, Y.shape[0])
X为输入值,Y为实际输出值。
params, cost_ = fit(X, Y, 0.3, 5, 5000)
本文中学习率设置为0.3,隐藏层神经元数量为5,迭代次数为5000.当然也可设置不同数值尝试。
下面画图以说明每次迭代中成本函数的变化。
import matplotlib.pyplot as pltplt.plot(cost_)
结果正确!
first_cost = 0.7383781203733911last_cost = 0.06791109327547613
完整代码:
import numpy as np
def sigmoid(x):
return (1 / (1 + np.exp(-x)))def setParameters(X, Y, hidden_size):
np.random.seed(3)
input_size = X.shape[0] # number of neurons in
input layer
output_size = Y.shape[0] # number of neurons in
output layer.
W1 = np.random.randn(hidden_size, input_size)*np.sqrt(2/input_size)
b1 = np.zeros((hidden_size, 1))
W2 = np.random.randn(output_size, hidden_size)*np.sqrt(2/hidden_size)
b2 = np.zeros((output_size, 1))
return {'W1': W1, 'W2': W2, 'b1': b1, 'b2': b2}def forwardPropagation(X, params):
Z1 = np.dot(params['W1'], X)+params['b1']
A1 = np.tanh(Z1)
Z2 = np.dot(params['W2'], A1)+params['b2'] y = sigmoid(Z2)
return y, {'Z1': Z1, 'Z2': Z2, 'A1': A1, 'y': y}
def cost(predict, actual): m = actual.shape[1]
cost__ = -np.sum(np.multiply(np.log(predict),
actual) + np.multiply((1 - actual),
np.log(1 - predict)))/m
return np.squeeze(cost__)
def backPropagation(X, Y, params, cache): m = X.shape[1]
dy = cache['y'] - Y
dW2 = (1 / m) * np.dot(dy, np.transpose(cache['A1']))
db2 = (1 / m) * np.sum(dy, axis=1, keepdims=True)
dZ1 = np.dot(np.transpose(params['W2']), dy) * (1-np.power(cache['A1'], 2))
dW1 = (1 / m) * np.dot(dZ1, np.transpose(X))
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
return {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}def
updateParameters(gradients, params, learning_rate = 1.2):
W1 = params['W1'] - learning_rate * gradients['dW1']
b1 = params['b1'] - learning_rate * gradients['db1']
W2 = params['W2'] - learning_rate * gradients['dW2']
b2 = params['b2'] - learning_rate * gradients['db2']
return {'W1': W1, 'W2': W2, 'b1': b1, 'b2': b2}
def fit(X, Y, learning_rate, hidden_size, number_of_iterations = 5000):
params = setParameters(X, Y, hidden_size)
cost_ = [] for j in range(number_of_iterations):
y, cache = forwardPropagation(X, params)
costit = cost(y, Y)
gradients = backPropagation(X, Y, params, cache)
params = updateParameters(gradients, params, learning_rate)
cost_.append(costit)
return params,
cost_# Testing the codeimport sklearn.datasetsX,
Y = sklearn.datasets.make_moons(n_samples=500, noise=.2)X,
Y = X.T, Y.reshape(1, Y.shape[0])params, cost_ = fit(X, Y, 0.3, 5, 5000)
import matplotlib.pyplot as pltplt.plot(cost_)
留言 点赞 关注
我们一起分享AI学习与发展的干货
欢迎关注全平台AI垂类自媒体 “读芯术”
(添加小编微信:dxsxbb,加入读者圈,一起讨论最新鲜的人工智能科技哦~)