LSTM+CRF介绍



LSTM和CRF要解决问题的：序列标注问题（中文分词、词性识别、命名实体识别、机器翻译等）

本文先介绍LSTM的基本结构，再介绍LSTM与CRF结合的方法（CRF的具体算法介绍不包括在本文中）。

LSTM是RNN的一种特殊形式，首先看一下RNN单元的基本结构定义：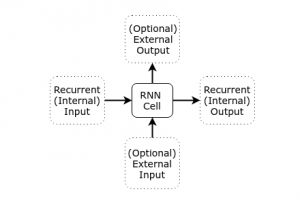

简单解释一下，RNN其实是希望能模拟人类大脑处理信息的方式，人类的大脑所接收的信号可以分为外部（即我们的感知，视觉、听觉等）和内部（脑海中已经存在的想法），在不同的时刻，大脑会使人产生新的行动（external output）和新的想法（internal output）。RNN网络其实是一组前向网络的组合，每个单元代表一个时间点，每个RNN单元（也有人叫细胞）有两种输入输出，分别代表RNN网络自身的输入输出，以及应对外部刺激的输入输出（可以看作是希望传递到下一时刻的状态）。按照这里提出的通用结构，理论上来说RNN可以完美的模拟人的大脑，但是实际训练起来并不是那么简单。主要问题大家都知道：RNN训练通常伴随着梯度衰退缓慢和梯度爆炸增长现象。LSTM正是为了解决这一问题而提出的。

LSTM设计的初衷是为了确保现实世界中信息的完整性，引入一个memory cell，即对历史信息进行记录，并且这个记录是有控制有选择的。由此引入了三个控制门的概念。这三个控制门分别控制LSTM单元应该写入什么、读取什么、输出什么。

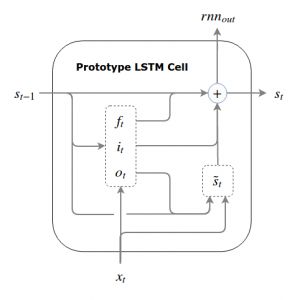
我们可以先看一下LSTM的原型结构：

其中，三个控制门的定义如下：

i t =σ(W i s t−1 +U i x t +b i )  it=σ(Wist−1+Uixt+bi)

o t =σ(W o s t−1 +U o x t +b o )  ot=σ(Wost−1+Uoxt+bo)

f t =σ(W f s t−1 +U f x t +b f )  ft=σ(Wfst−1+Ufxt+bf)

s t  ~ =ϕ(W(o t ⊙s t−1 )+Ux t +b)  st~=ϕ(W(ot⊙st−1)+Uxt+b)

s t =f t ⊙s t−1 +i t ⊙s t  ~   st=ft⊙st−1+it⊙st~

 

这里跟最开始的RNN模型进行对比，可以发现， s t−1   st−1 是内部输入，可以看做是前一时刻的状态， x t   xt 是当前输入，前一状态和当前输出决定了门的控制方式，进而通过三个控制门去控制输出 rnn out   rnnout 和更新当前状态 s t   st 。

但是这个原型有个很明显的问题，就是状态值 s t   st 是无界的，在训练刚开始的时候，由于各项权重值都是随机初始化的，并且 o t   ot 和 f t   ft 是无关的，导致状态值很容易变得很大并且是杂乱的，使得门和输出候选集合都会很容易饱和，因而需要给状态值加上限制范围。有很多LSTM的变体可以克服这个问题，最简单的通过归一化可以实现，另外GRU（Gated Recurrent Unit）结构也可以避免这个问题，或者是引入非线性变换的方法。

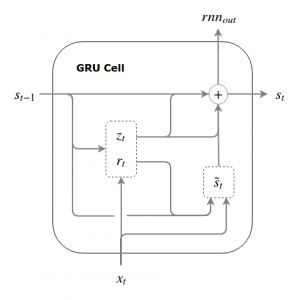
很多人会把GRU看作是LSTM的一个简化，因为它将写入门和记忆门进行了关联，最终相当于只使用了两个门，在GRU结构中被称作update gate和reset gate。

这两个门的定义如下：

r t =σ(W r s t−1 +U r x t +b r )  rt=σ(Wrst−1+Urxt+br)

z t =σ(W z s t−1 +U z x t +b z )  zt=σ(Wzst−1+Uzxt+bz)

s t  ~ =ϕ(W(r t ⊙s t−1 )+Ux t +b)  st~=ϕ(W(rt⊙st−1)+Uxt+b)

s t =z t ⊙s t−1 +(1−z t )⊙s t  ~   st=zt⊙st−1+(1−zt)⊙st~

 

这里相当于把写入门和记忆门认为是负相关的，这样就能尽可能稳定状态值。

引入非线性变换的方法，我们这里定义为伪LSTM结构，即对状态值进行sigmod或tanh等类型的非线性变换，使用变换后的值来更新控制门和候选输出，最终的rnn输出也使用变换后的，但是要注意，在更新状态值的时候，仍然使用变换前的状态值，这同样可以达到限制状态值范围的作用。

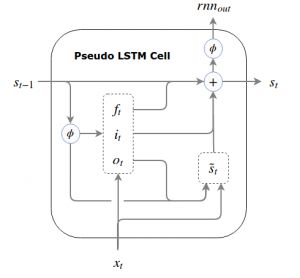
伪LSTM的单元结构如下：

对应公式如下：

i t =σ(W i (ϕ(s t−1 ))+U i x t +b i )  it=σ(Wi(ϕ(st−1))+Uixt+bi)

o t =σ(W o (ϕ(s t−1 ))+U o x t +b o )  ot=σ(Wo(ϕ(st−1))+Uoxt+bo)

f t =σ(W f (ϕ(s t−1 ))+U f x t +b f )  ft=σ(Wf(ϕ(st−1))+Ufxt+bf)

s t  ~ =ϕ(W(o t ⊙ϕ(s t−1 ))+Ux t +b)  st~=ϕ(W(ot⊙ϕ(st−1))+Uxt+b)

s t =f t ⊙s t−1 +i t ⊙s t  ~   st=ft⊙st−1+it⊙st~

rnn out =ϕ(s t )  rnnout=ϕ(st)

 

伪LSTM和通常定义的基本LSTM的区别主要有三个：

1.LSTM是在写入之后才读取，这样迫使LSTM网络中各单元之间需要有隐藏层；

2.在计算控制门的时候，使用的是门控隐状态 h t−1 =o t−1 ⊙ϕ(c t−1 )  ht−1=ot−1⊙ϕ(ct−1) ，而不是非线性变换后的主状态 ϕ(c t−1 )  ϕ(ct−1)

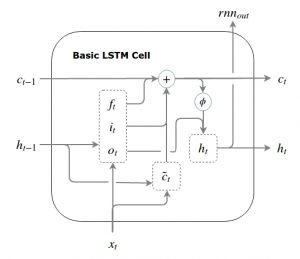
3.LSTM的外部输出是门控隐状态 h t =o t ⊙ϕ(c t )  ht=ot⊙ϕ(ct) ，而不是非线性变换后的主状态 ϕ(c t )  ϕ(ct) 故而基本的LSTM单元结构如下：

i t =σ(W i h t−1 +U i x t +b i )  it=σ(Wiht−1+Uixt+bi)

o t =σ(W o h t−1 +U o x t +b o )  ot=σ(Woht−1+Uoxt+bo)

f t =σ(W f h t−1 +U f x t +b f )  ft=σ(Wfht−1+Ufxt+bf)

c t  ~ =ϕ(Wh t−1 +Ux t +b)  ct~=ϕ(Wht−1+Uxt+b)

c t =f t ⊙c t−1 +i t ⊙c t  ~   ct=ft⊙ct−1+it⊙ct~

h t =o t ⊙ϕ(c t )  ht=ot⊙ϕ(ct)

rnn out =h t   rnnout=ht

 

还有一种LSTM的变体，也是目前比较常用的结构，即LSTM with peepholes，在控制门中也引入前一时刻的状态，如下：

i t =σ(W i h t−1 +U i x t +P i c t−1 +b i )  it=σ(Wiht−1+Uixt+Pict−1+bi)

f t =σ(W f h t−1 +U f x t +P f c t−1 +b f )  ft=σ(Wfht−1+Ufxt+Pfct−1+bf)

c t  ~ =ϕ(Wh t−1 +Ux t +b)  ct~=ϕ(Wht−1+Uxt+b)

c t =f t ⊙c t−1 +i t ⊙c t  ~   ct=ft⊙ct−1+it⊙ct~

o t =σ(W o h t−1 +U o x t +P o c t +b o )  ot=σ(Woht−1+Uoxt+Poct+bo)

h t =o t ⊙ϕ(c t )  ht=ot⊙ϕ(ct)

rnn out =h t   rnnout=ht

 

上述介绍了LSTM单元结构，LSTM网络是多个LSTM单元结构的组合，目前常用的双向LSTM网络通常通过是使用两层LSTM，在反向层将输入反向实现的。

通过LSTM网络的处理，相当于得到了一个比较好的对输入数据的表示方法，LSTM单元最终输出的向量即可以看成是输入数据的一种表示形式，最终在打标签阶段，一般都采用softmax进行处理，不过这种方法在处理输出标签直接有强烈关系的数据时，效果还是有限的。特别是在实际的序列标注任务时，由于神经网络结构对数据的依赖很大，数据量的大小和质量也会严重影响模型训练的效果，故而出现了将现有的线性统计模型与神经网络结构相结合的方法，效果较好的有LSTM与CRF的结合。简单来说就是在输出端将softmax与CRF结合起来，使用LSTM解决提取序列特征的问题，使用CRF有效利用了句子级别的标记信息。

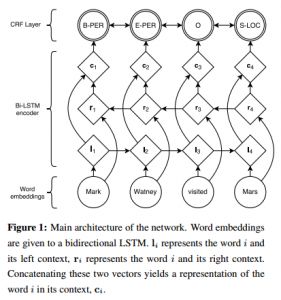
如下是用于实体识别的LSTM+CRF模型结构：

在LSTM+CRF模型下，输出的将不再是相互独立的标签，而是最佳的标签序列。

对于输入： X=(x 1 ,x 2 ,...,x n )  X=(x1,x2,...,xn) ，

我们可以定义LSTM的输出概率矩阵 P n∗k   Pn∗k 其中k是输出标签的个数。 P i,j   Pi,j 是指第i个字被标记为第j个标签的概率。对于待预测的标签序列： y=(y 1 ,y 2 ,...,y n )  y=(y1,y2,...,yn) ，

我们可以有如下定义：

s(X,y)=∑ n i=0 A y i ,y i+1  +∑ n i=0 P i,y i    s(X,y)=∑i=0nAyi,yi+1+∑i=0nPi,yi

 

其中A是状态转移矩阵， A i,j   Ai,j 代表从第i个tag转移到第j个tag的概率。

通过求得最大的 s(X,y)  s(X,y) ，即可得到最佳的输出标签序列。这里引入的CRF，其实只是对输出标签二元组进行了建模，然后使用动态规划进行计算即可，最终根据得到的最优路径进行标注。

参考文献：

1.http://r2rt.com/written-memories-understanding-deriving-and-extending-the-lstm.html

2.Bidirectional LSTM-CRF Models for Sequence Tagging（https://arxiv.org/abs/1508.01991）

3.Neural Architectures for Named Entity Recognition（https://arxiv.org/abs/1603.01360）

4.http://www.jianshu.com/p/9dc9f41f0b29