《算法笔记》学习笔记 part1
一. 前言
我开始写这篇笔记时,2019年研究生考试已经过去一周了,虽然还不知道初试结果,但还是要开始准备复试了。复试中机试又占了很大的比例,故这里开始复习算法知识了,主要用书为《算法笔记》。
这份笔记将主要分两个部分。本篇笔记为part1。主要包括两个内容,一是我觉得有必要记录的知识点;另外就是一些专题,内容是一些归纳和自己的思考。
希望能顺利的通过复试(如果过了初试的话...)
二. 知识点部分
【引】这里记录一些小知识点
1.变量类型范围问题:简单来说,看到题目要求10的9次方以内时,用int;若是10的18次方以内,用long long。其中大于2^31-1的话就要再在数值后加上LL。另外,对于浮点型,根本不要用float,直接上double。
2.字符与ASCII:小写字母比大写字母的ASCII码值大32,eg:a为97,A为65。另外,字符在计算机内部就是按照ASCII码来存储的,所以char c = 97这句话就相当于char c = 'a'。还要注意大小写怎么转换,其实就是加或减32的问题,当然也可以用toupper()和tolower(),需要iostream的头函数(其实是ctype)
3.定义常量的两种方式:eg1:#define pi 3.14 eg2:const double pi = 3.14。
【注】p13“宏定义陷阱”,如define Add(a, b) ((a)+(b)),具体不赘述,总之就是要加上尽可能多的括号。
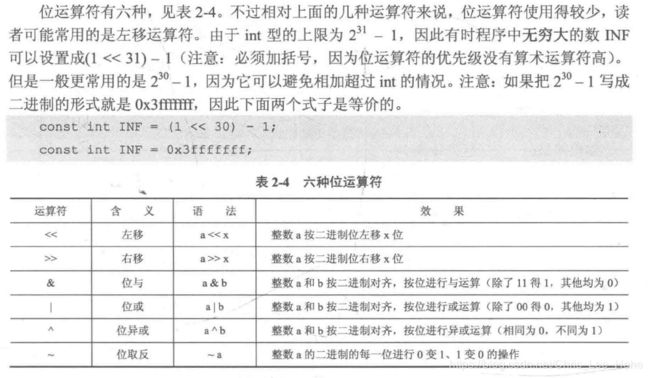
4.位运算符:见下图
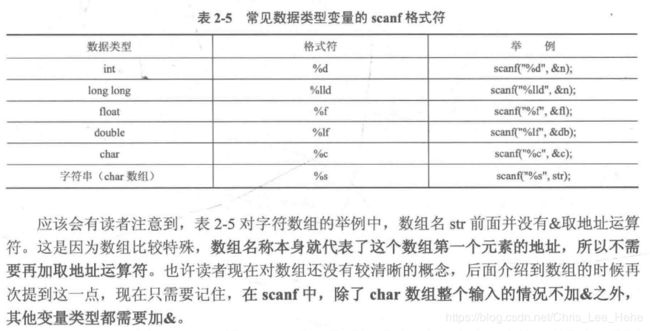
5.Scanf中用到的“&”:变量在定义后,会在计算机内存中分配一块空间给这个变量,为了得到这个变量的地址,需要加上这个&。其他还需提醒的在下图中:
【注】除了%c之外,scanf对其他格式符的输入是以空白符(空格,换行等)为结束判断标志的。举个例,看下面这段代码:
由于字符可以读入空格和换行,所以空格被当作了c的值,而str会把空格当作结束,所以a就成了str。
6. %md, %0md, %.mf的作用(p22)
7.一些常用math函数
floor(x):向下取整 ceil(x):向上取整
pow(a, b):求a的b次方 sqrt(x):求根号
log(x):即求lnx,若要求以a为底的,则必须利用公式:lnb/lna 来替换
pi的精确定义为acos(-1.0)
8.while和do...while:后者会先执行循环体一次,再去判断循环条件是否为真,这就使得其实用性不如前者。
9.对于一个很大的数组(10^6级别),则需要将其定义在主函数外面,否则会异常退出。
10.memset:对于一个数组(如{1,2,3,4,5}),可利用memset(a, 0, sizeof(a))这句代码来让所有元素值置0,注意使用这个函数最好只把值置为0或-1,具体原因见p46
11.字符数据输入输出三种方式:
| scanf & printf | 注意输入时,%c能识别空格和换行并将其输入,而%s则将其当作结束 |
| getchar & putchar | 用以输入输出单个字符 |
| gets & puts | 用以输入输出一行字符串。注意gets()会将\n作为输入结束,所以scanf完一个整数后,若要用gets,需先用getchar接收整数后的换行符。 |
【注1】由于字符串结束符\0ASCII码为0,占用一个字符位,因此开字符数组时千万记得字符数组长度一定要比实际存储字符串长度至少多1个。
【注2】若不是使用scanf(%s格式)或gets输入字符串,则一定要在输入字符串后加'\0',不然printf或puts输出会无法识别字符串末尾而导致输出乱码。
12.string.h含有的几个函数
| strlen() | 得到字符数组的长度(不算'\0') |
| strcmp() | 返回两个字符串大小的比较结果(按照字典序) |
| strcpy() | 字符串复制,eg:strcpy(str1, str2),即把1复制到2 |
| strcat() | 把一个字符串接到另一个字符串后面,eg:strcat(str1, str2),注意是把2接到1之后 |
13.sscanf和sprintf:这两个是处理字符串问题的利器,具体可见p53-54,这里贴两个例子:
14.以数组作为函数参数要注意的点:首先是参数中数组的第一维不需要填写长度,若是二维,则第二维需填写;其次,当数组作为参数时,在函数中对数组元素的修改相当于是对原数组元素的修改,这一点和普通局部变量不同。
15.关于STL,实在是为我们省了很多力气。STL里的容器就像是Python里的列表,字典,元祖,集合这四种基本数据结构一样,可以方便的解决很多问题。这部分内容由于很多,我就只列出《算法笔记》上说到的一些方法吧:
| 容器 | 简介 | 常用函数(i一般指值,it一般指迭代器) |
| vector | 变长数组,长度根据需要自己变化;一般用于在元素个数不确定时节省空间 | push_back(x):在最后添加一个元素 |
| pop_back(x):删除尾元素 | ||
| size():获取长度 | ||
| clear():清除所有 | ||
| insert(it, x):在it处插入x | ||
| erase(it):删除it处的元素(erase有多种删除方式) | ||
| set | 就是个集合 | insert(x):插入x |
| find(value):找值为value的迭代器 | ||
| erase(it):删除it处的元素(erase有多种删除方式) | ||
| size():获取长度 | ||
| clear():清除所有 | ||
| string | 专门用于字符串处理的容器,好用的很! | string之间可以直接加减,比较 |
| length()/size() | ||
| insert(pos, string):在pos号位置插入string(还有其他写法) | ||
| erase(it):删除it处的元素(erase有多种删除方式) | ||
| clear():清除所有 | ||
| substr(pos, len):返回从pos开始长为len的子串 | ||
| string::npos:find()失配时的默认值 | ||
| find(str2):找字串str2的初始位置(有多种写法) | ||
| replace(pos, len, str2):把str从pos开始,长为len的字串替换为str2(有多种写法) | ||
| map | 就是个字典 | find(key):找到key的迭代器 |
| erase(it):删除it处的元素(erase有多种删除方式) | ||
| size():获取长度 | ||
| clear():清除所有 |
三. 专题部分
专题一:类型转换
【引】在刷题过程中遇到过很多需要将“数字”,“字符”,“字符串”这三种类型互相转换,故这里做个小结。
1.string --> char数组(如果要使用printf输出,那么string必须先转化为char数组)
string b;
printf("%s", b.c_str())2.char数组 --> string (这个倒是不常用,我处理字符串现在基本用string了,但还是记录一下)
char a[] = "haha";
string b(a); //直接初始化3.数字 --> 字符(这个之前提过,就是+‘0’和-‘0’的事情)
4.数字 --> 字符串(我现在大致有两种方法,如下:)
//法一
int a = 123;
string b;
stringstream ss;
ss << a;
b = ss.str();
//法二(只能是int --> char数组)
int a = 123;
char b[10] = {0}; //注意这个数组长度需稍微设置大一些,不然报错
itoa(a, b, 10); //a为需转换的值,b为转换后放的地址,10为10进制的意思
5.字符串 --> 数字(同样有两种方法,如下:)
//法一
string a = "123";
int b;
stringstream ss;
ss << a;
ss >> b;
//法二
char a[] = "123";
int b = atoi(a);【注】需注意的是,itoa和atoi都是针对整型和字符串的,如果是浮点型,那就是ftoa和atof。另外,对于stringstream ss要注意,如果你要用到它不止一次,在使用一次之后需要使用ss.clear(); ss.str(""); 来清空缓冲区(这两个函数最好一起用)
专题二:数学问题
1.素数:主要了解如何判断一个数字是否是素数。
bool is_Prime(int n){
if(n <= 1) return 0;
int sqr = (int)sqrt(n * 1.0);
for(int i=2; i<=sqr; i++)
if(n % i == 0)
return 0;
return 1;
}【注】埃式筛法也不难,但是感觉一般用不到。(算法笔记p162)
2.最大公约数:记住gcd(a, b) = gcd(b, a%b);
int gcd(int a, int b){
if(b == 0)
return a;
else
return gcd(b, a % b);
}3.分数:关于分数最重要的就是3条规则,如下代码(其中列出了减法的代码,加,减,乘均类似)
int gcd(int a, int b){
if(b==0) return a;
return gcb(b, a % b);
}
struct Fraction{
int up, down;//分子 分母
};
Fraction reduction(Fraction res){
if(res.down < 0){//规则1:负号只放在分子
res.down = -res.down;
res.up = -res.up;
}
if(res.up == 0)//规则2:分母不为0
res.down = 1;
else{
int k = gcd(abs(res.up), abs(res.down));//规则3:化简(分子分母没有1之外的公约数),注意abs
res.up /= k;
res.down /= k;
}
return res;
}
Fraction minu(Fraction a, Fraction b){ //分数减法
Fraction res;
res.up = a.up*b.down - a.down*b.up;
res.down = a.down * b.down;
return reduction(res);
}
4.进制转换:掌握将P进制转化为10进制,以及10进制转化为Q进制即可。(算法笔记P93)
5.复数运算:参考(https://blog.csdn.net/qq_35194071/article/details/82014561)
6.大整数运算:对于大整数就需要用int数组来存每一位。
专题三:排序
【引】这里我先把在复习数据结构时做的九大排序的表格列出来,可以说是一目了然了。
1.冒泡排序
#include
int main(){
int a[10] = {3,2,4,3,7,5,8,6,0,10};
for(int i=1;i<10;i++){ //这里要注意i因为是第几趟的含义,要从1开始
for(int j=0;j<10-i;j++){
if(a[j] > a[j+1]){
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
for(int i=0;i<10;i++)
printf("%d\n", a[i]);
}