图像增强：直方图正规化、直方图均衡 (python实现)

当图像灰度级范围较小时，会造成图像对比度较低的问题。而图像增强则是通过把图像的灰度级范围进行扩大，从而使图像细节看起来更加清晰。下面我们一步一步进行说明。

灰度直方图

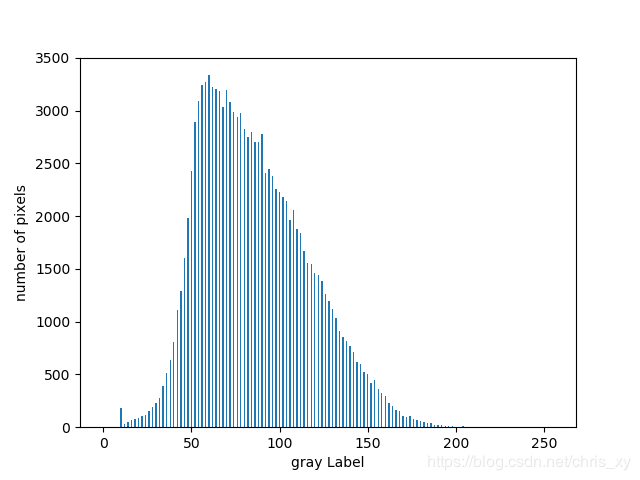
直方图是对灰度图像上的灰度值进行统计得到的关于灰度值的函数，用来描述每个灰度值在图像矩阵的像素个数或占有率。以下面的植物图片为例：

import cv2
import matplotlib.pyplot as plt
# 绘制图像灰度直方图
def deaw_gray_hist(gray_img):
    '''
    :param  gray_img大小为[h, w]灰度图像
    '''
    # 获取图像大小
    h, w = gray_img.shape
    gray_hist = np.zeros([256])
    for i in range(h):
        for j in range(w):
            gray_hist[gray_img[i][j]] += 1
    x = np.arange(256)
    # 绘制灰度直方图
    plt.bar(x, gray_hist)
    plt.xlabel("gray Label")
    plt.ylabel("number of pixels")
    plt.show()
# 读取图片
img = cv2.imread(img_path) # 这里需要指定一个 img_path
deaw_gray_hist(img[:,:,0])
cv2.imshow('ori_img', img)
cv2.waitKey()

如下所示，左边为植物图片，右边为其对应的灰度直方图。从直方图可以看出其灰度值主要聚集在范围很小的一个区域里，所以导致植物图片对比度较低，不太清晰。

      

线性变换

我们把图像的灰度直方图看做是关于图像灰度值的一个函数，即每张图片都可以得到一个关于其灰度值的分布函数。我们可以通过线性变换让其灰度值的范围变大。
假设图片上某点的像素值为 $i$，经过线性变换后得到的像素值为 $o$ , $a,b$ 为线性变换的参数则：
$$o=a\ast i+b$$
其中当 $a>0$ 时，图片的对比度会增大；当 $0<a<1$时，图片的对比度会减小。当 $b>0$ 时，图片的亮度会增大；当 $b<0$时，图片的亮度会减小。

# 对图像进行 线性变换
def linear_transform(img, a, b):
    '''
    :param img: [h, w, 3] 彩色图像
    :param a:  float  这里需要是浮点数，把图片uint8类型的数据强制转成float64
    :param b:  float
    :return: out = a * img + b
    '''
    out = a * img + b
    out[out > 255] = 255
    out = np.around(out)
    out = out.astype(np.uint8)
    return out
# a = 2, b=10
img = linear_transform(img, 2.0, 10)
deaw_gray_hist(img[:, :, 0])
cv2.imshow('linear_img', img)
cv2.waitKey()

      

直方图正规化

设图片$I$的灰度值范围为$[I_{min},I_{max}]$，而输出图片$O$的灰度值范围$[O_{min},O_{max}]$，当前图片第$r$行第$c$列的灰度值表示为$I_{r,c}$，同样输出图片对应位置的灰度值表示为$O_{r,c}$，它们之间的映射关系为：
$$\frac{O_{r,c}-O_{min}}{I_{r,c}-I_{min}}=\frac{O_{max}-O_{min}}{I_{max}-I_{min}}$$
该式子可以转换为：
$$\begin{gathered} O_{r,c}=\frac{O_{max}-O_{min}}{I_{max}-I_{min}}\ast (I_{r,c}-I_{min})+O_{min} \\ =(\frac{O_{max}-O_{min}}{I_{max}-I_{min}})\ast I_{r,c}+(O_{min}-\frac{O_{max}-O_{min}}{I_{max}-I_{min}}\ast I_{min}) \end{gathered}$$
该式子最后可以转换成线性变换的形式，直方图正规化是一种自动选择a和b值的一种线性变换方法。

def normalize_transform(gray_img):
    '''
    :param gray_img:
    :return:
    '''
    Imin, Imax = cv.minMaxLoc(gray_img)[:2]
    Omin, Omax = 0, 255
    # 计算a和b的值
    a = float(Omax - Omin) / (Imax - Imin)
    b = Omin - a * Imin
    out = a * gray_img + b
    out = out.astype(np.uint8)
    return out
    
b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
b_out = normalize_transform(b)
g_out = normalize_transform(g)
r_out = normalize_transform(r)
nor_out = np.stack((b_out, g_out, r_out), axis=-1)
deaw_gray_hist(nor_out[:, :, 0])
cv.imshow('nor_out', nor_out)
cv2.waitKey()

因为植物原图本身的灰度值范围就很接近$[0,255]$，所以经过直方图正规化后效果并不明显。

      

直方图均衡

直方图均衡步骤如下：

1. 计算图像的灰度直方图
2. 计算灰度直方图的累加直方图
3. 得到输入灰度级和输出灰度级之间的映射关系

设输入的灰度级为 $p$，输出的灰度级为 $q$。
$$\frac{q+1}{256}=\frac{{\sum }_{k=0}^{p}his{t}_k}{H\ast W}$$

# 对图像进行 均衡化
def equalize_transfrom(gray_img):
    return cv.equalizeHist(gray_img)
    
b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
b_out = equalize_transfrom(b)
g_out = equalize_transfrom(g)
r_out = equalize_transfrom(r)
equa_out = np.stack((b_out, g_out, r_out), axis=-1)
deaw_gray_hist(equa_out[:, :, 0])
cv.imshow('equa_out', equa_out)
cv2.waitKey())

      

参考链接：
OpenCV–Python 图像增强