图的最短路径算法分析与总结
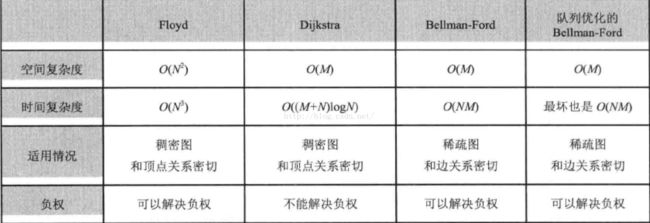
图的求最短路径算法大类可以分为4种,在这里一一介绍
1.Floy算法
2.Dijkstra算法
3.Bellman-Ford算法
4.Bellman-Ford算法的队列优化
注:以下程序是以编号为1的节点为源点的程序,如果需要更改,可以自行更改。
一, Floy算法
基本思想:
1.数据结构:邻接矩阵
2.算法思想:动态规划
核心代码:
for(k=1;k<=n;k++)
{
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(e[i][k]+e[k][j]e[i][j]是表示从i节点到j节点的距离
如果I=2,j=7;
其前面的已经是最优解,只需判断一下经过哪个节点最小。
注:邻接矩阵的建立:
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(i==j) e[i][j]=0;
else e[i][j]=999999;
}
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&x,&y,&v);
e[x][y]=v;
}
二. Dijkstra算法
数据结构:邻接矩阵
算法思想:基于贪心算法
核心代码:
for(i=1;idis[u]+e[u][v])
{
dis[v]=dis[u]+e[u][v];
}
}
}
}
这个算法不能解决负边权问题
主要思想:
1.找到当前里源点最近的点,然后把其值改为确定值
原因:因为再经过任何一边都会增加其值,所以其值一定最小,这也是为什么其不能解决负边权问题的原因。
2.用选择法更新每个点,如果某个点经过这个点路径会减小,则更新那个点,否则则不更新
3.不断重复1.2步骤,直到其所有点都已经成为标记值
三,bellman- ford算法
数据结构:数组
算法思想:遍历利用边 ”松弛“
核心代码:
for(k=1;k<=n-1;k++)
{
for(i=1;i<=m;i++)
{
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
}
}
该算法是以边为主要思想的遍历每个边,每一个边选择或者不选择,每个选择的边都进行了一遍 “松弛”
每松弛第i次就代表着从出发点开始,经过i条边所能达到的最小距离,所以在没有环的情况下,只需走n-1次
所以有n-1次循环外层
如果有环,如果是负边权的,则其没有最小值,如果是正边权,这其不必经过环,
那下面讨论一下怎么确定其是否有负边权的环:当循环n-1次后,如果继续循环其还变化的话,就说明有负边权的环,否则其没有负边权的环
代码如下:
int flag=0;
for(i=1;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i]) flag=1;
if(flag) printf("there are loop in the map!!");
四,bellman-ford算法的队列优化
基本思想:利用队列实现了bellman-ford算法的核心思想,就是代码长度增加,代码理解起来相对难,但是减少了时间复杂度,减少了bellman-ford里面不必要的循环。
数据结构:队列,数组
个人理解:其有点像广度优先搜索,和动态规划
由于会比较难理解,就上全部代码:
#include
#include
#include
int main()
{
int n,m,i,j,k;
int u[8],v[8],w[8],e[100][100]={0};
int first[6],next[8];
int dis[6]={0},book[6]={0};
int que[101]={0},head=1,tail=1;
int inf =99999;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++) dis[i]=inf;
dis[1]=0;
memset(book,0,sizeof(book));
for(i=1;i<=n;i++) first[i]=-1;
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&u[i],&v[i],&w[i]);
e[u[i]][v[i]]=w[i];
//very beautiful solution
//very important ! ! //就是一条边指向另一条边
next[i]=first[u[i]];//判断是否有与第i条边有相同节点的边,有的话就把该边赋给next[i]
first[u[i]]=i;//把边的序号赋值给first的第节点个个的元素
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
printf("%5d",e[i][j]);
}
printf("\n");
}
printf("\n");
for(i=1;i<=m;i++) printf("%d ",first[i]);
printf("\n");
for(i=1;i<=m;i++) printf("%d ",next[i]);
printf("\n");
que[tail]=1; tail++;
book[1]=1;
while(headdis[u[k]]+w[k])//k代表第几条边
{
dis[v[k]]=dis[u[k]]+w[k];
if(book[v[k]]==0)
{
que[tail]=v[k];
tail++;
book[v[k]]=1;
}
}
k=next[k];
}
book[que[head]]=0;
head++;
}
for(i=1;i<=n;i++) printf("%5d",dis[i]);
getch();
return 0;
}
代码分析:
1.邻接表的两个数组储存:
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&u[i],&v[i],&w[i]);
e[u[i]][v[i]]=w[i];
//very beautiful solution
//very important ! ! //就是一条边指向另一条边
next[i]=first[u[i]];//判断是否有与第i条边有相同节点的边,有的话就把该边赋给next[i]
first[u[i]]=i;//把边的序号赋值给first的第节点个个的元素
}
先大概分析一下代码:
首先first数组里面存的数据会被覆盖,所以其存储的数据必定是最后一个数据,因为其前面的数据都被覆盖掉了。
然后next数组里面储存的数据不会被覆盖,而且其储存的肯定是与第i个边有相同头结点的边的编号,而且其比i小且为最临近的一条边,因为再前面的边的编号已经被覆盖。
来看下实例,就会进一步理解!
先来数据:
测试数据:
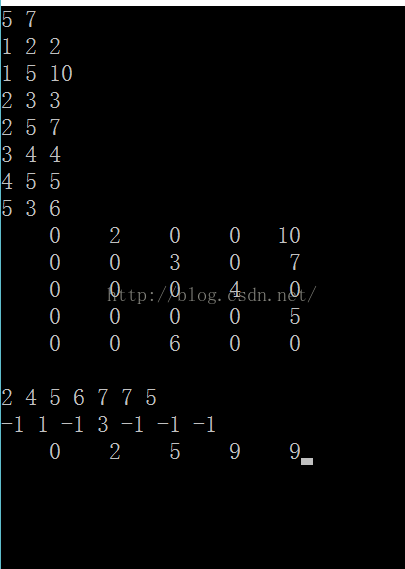
5 7 //5个顶点,7条边
1 2 2
1 5 10
2 3 3
2 5 7
3 4 4
4 5 5
5 3 6
| first[] | 2 4 5 6 7 7 5 |
| next[] |
-1 1 -1 3 -1 -1 1
|
这就是其运行结果。
可以分析出:first[]数组第i个元素代表编号为i点所在的最后一个边的编号
next[]第i个元素代表与第i个边有相同前结点的 由大到小离i边编号最近的 一个边的 编号
可以看出,其用两个数组存储邻接表,然后就是如何利用这个数据结构了
来看代码:
while(headdis[u[k]]+w[k])//k代表第几条边
{
dis[v[k]]=dis[u[k]]+w[k];//同bellman-ford算法思想
if(book[v[k]]==0)
{
que[tail]=v[k];//入队
tail++;
book[v[k]]=1;//标记
}
}
k=next[k];//利用其找到有相同前节点的边的编号
}
book[que[head]]=0;//出队,并标记
head++;
}
因为这个算法用队列实现的,所以从源点开始,每遇到一个“新‘’节点入队,同时处理入队的节点,每处理完一个节点,该节点出队。
这里的”新”是指”队列“中不存在的节点
实现方法:用book[]数组标记
当队列为空时,代表着其已经处理完所有的数据,结束计算,输出。
到此四个计算最短路径的算法已经介绍完,其中应用的最主要的思想就是动态规划,即当前解为最优解。
然后就是Dijkstra算法中应用的贪心算法(导致其只能用于没有负边权的图)
Floy和Dijkstra算法中是以节点为中心,运用邻接矩阵
Bellman-ford 和Bellman-ford的队列优化 是以边为中心并继承Dijkstra的dis[]一维数组
先写这些了,,以后有发现再补上!