Numpy实战：numpy + matplotlib 简易绘制 股票布林带

这篇文章，我们采用numpy + matplotlib 的结合简易的绘制股票的布林带，在此之前，我们先说几个有关函数的应用。

Numpy卷积
在数学中，卷积可以被看做移动平滑的推广。
在numpy 中数组也可以做卷积。
这里我们只涉及一维卷积。
numpy.convolve(a, v, mode=‘full’)
mode可取 ‘full’ (完全卷积), ‘same’ (同维卷积), ‘valid’ (有效卷积)

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
a = np.array([1, 2, 3, 4, 5])
b = np.array([6, 7, 8])
print(np.convolve(a, b))
print(np.convolve(a, b, 'same'))
print(np.convolve(a, b, 'valid'))

[ 6 19 40 61 82 67 40]     #完全卷积
[19 40 61 82 67]           #同维卷积
[40 61 82]                 #有效卷积

其内部运算如下


得        6    19   40   61   82   67   40
0    0    1    2    3    4    5    0    0
8    7    6
     8    7    6
          8    7    6
               8    7    6
                    8    7    6
                          8   7    6
                              8    7    6

取a数组元素个数时为同维卷积
取b数组个数时为有效卷积
注: 运算时b数组顺序是反过来的

这是接下来要导入的苹果公司某年某月的收盘价与日期

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import datetime as dt
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as md


# 将日-月-年格式的日期变为年-月-日格式的转换器函数
def dmyToymd(dmy):

    # 将UTF-8编码的字节串转换为UCS-4编码字符串
    dmy = str(dmy, encoding='utf-8')

    
    # 将日-月-年格式的日期字符串解析为datetime 类型的对象，再取其date类型的日期子对象
    date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
    
    # 将date类型的日期对象格式
    # 化为年-月-日形式的字符串
    ymd = date.strftime('%Y-%m-%d')
    return ymd


# 从aapl.csv文件中读取苹果公司一段时间内的日期和收盘价
dates, closing_prices = np.loadtxt(
    './data/aapl.csv', delimiter=",",
    usecols=(1, 6), unpack=True,
    dtype='M8[D], f8', converters={1: dmyToymd})

#五日均线数组，初始化
#因为第一个移动均线上的点要用前5个点来算，故均线上的点只有26个
sma51 = np.zeros(closing_prices.size - 4)

for i in range(sma51.size):
    #移动均线上的每个点都是用收盘价的5个点算，故第i个点就是收盘价数组中的 i 到 i+5 个点
    sma51[i] = closing_prices[i:i + 5].mean()
    
#移动均线上的每个点都是用收盘价的5个点算，因此我们可以把它看做收盘价数组与一个有5个5分之一的数组做卷积运算。
sma52 = np.convolve(closing_prices,np.ones(5) / 5, 'valid')

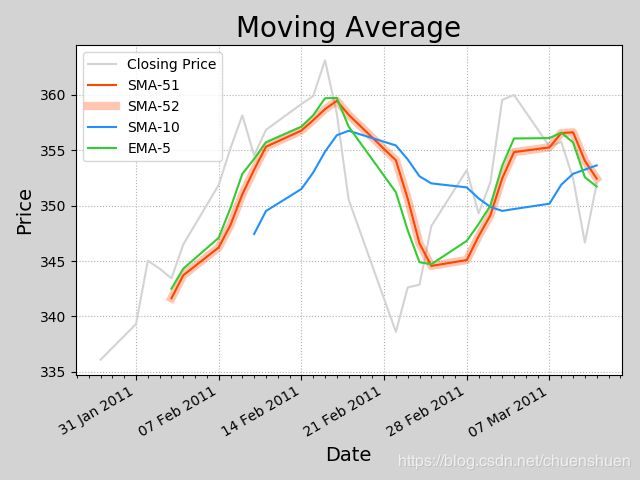
#由图中不难看出移动均线有一定的时间滞后性
#为突出这一点我们可以来绘制一条10日均线
sma10 = np.convolve(closing_prices,np.ones(10) / 10, 'valid')

#生成权重指数数组
weights = np.exp(np.linspace(-1, 0, 5))

#对权重进行归一化
weights /= weights.sum()

#5日权重均线，因为卷积会将卷积数组逆反，所以我们提前将卷积数组取反
ema5 = np.convolve(closing_prices, weights[::-1], 'valid')

plt.figure('Moving Average', facecolor='lightgray')
plt.title('Moving Average', fontsize=20)
plt.xlabel('Date', fontsize=14)
plt.ylabel('Price', fontsize=14)
ax = plt.gca()
# 主刻度表示每个星期的星期一
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
# 次刻度表示每一天
ax.xaxis.set_minor_locator(md.DayLocator())
# 设置主刻度的标签格式：日 月(英文缩写) 年
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
# Numpy.datetime64[D]   转换为  Matplotlib.dates.datetime.datetime
dates = dates.astype(md.datetime.datetime)

#绘制收盘价
plt.plot(dates, closing_prices, c='lightgray', label='Closing Price')
#绘制5日均线
plt.plot(dates[4:], sma51, c='orangered',label='SMA-51')
#用卷积方法绘制5日均线
plt.plot(dates[4:], sma52, c='orangered', alpha=0.3,linewidth=6, label='SMA-52')
#绘制10日均线
plt.plot(dates[9:], sma10, c='dodgerblue', label='SMA-10')

#绘制5日指数移动平均线
plt.plot(dates[4:], ema5, c='limegreen', label='EMA-5')
#由图中我们可以看到使用指数权重绘制的5日均线比只使用平均值计算 的均线时间滞后性上要更好。
#图例
plt.legend()
plt.gcf().autofmt_xdate()
plt.show()

如图：