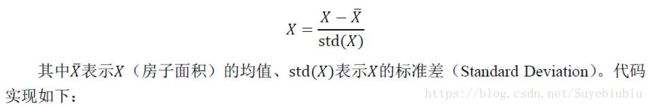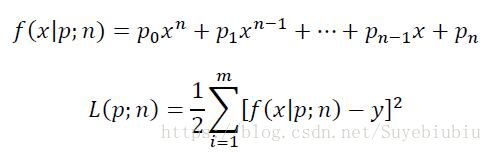1.1机器学习绪论
(1)什么是机器学习?
机器学习是一种让计算机利用数据而非指令来进行各种工作的方法。
机器学习是一个计算机程序,针对某个特定的任务,从经验中学习,且越做越好。
机器学习在统计理论下的、比较深刻的本质:它追求的是合理的假设空间(Hypothesis Space)的选取和模型的泛化(Generalization)能力。
- “假设空间”===>模型在数学上的“适用场合”
- “泛化能力”===>模型在未知数据上的表现
(2)机器学习常用术语
- “数据集”(Data Set),即数据的集合。其中每一条单独的数据被称为“样本”(Sample)。
- 数据集中的样本之间在各个意义下应该相互独立。
- 对于每个样本,它通常具有一些“属性”(Attribute)或者说“特征”(Feature),特征所具体取的值就被称为“特征值”(Feature Value)。
- 特征和样本所生成的空间被称为“特征空间”(Feature Space)和“样本空间”(Sample Space),可以把它们简单地理解为特征和样本“可能存在的空间”。
- 相对应的,“标签空间”(Label Space)用于描述模型的输出“可能存在的空间”;当模型是分类器时,将其称之为“类别空间”。
其中,数据集又可以分为以下3类:
- 训练集(Training Set):用来训练模型。
- 测试集(Test Set):用来测试、评估模型泛化能力。
- 交叉验证集(Cross-Validation Set,CV Set):用来调整模型具体参数。
(3)机器学习的分类 有监督学习/无监督学习
(3-1)有监督学习(Supervised learning) 可分为“回归”和“分类”
通过大量已知的输入和输出相配对的数据,让计算机从中学习出规律,从而能针对一个新的输入做出合理的输出预测。
- 在回归问题(Regression learning)中,我们会预测一个连续值。也就是说我们试图将输入变量和输出用一个连续函数对应起来;
- 在分类问题(Classification learning)中,我们会预测一个离散值(0,1,2...N),我们试图将输入变量与离散的类别对应起来。
每个数据点都会获得标注,如类别标签或与数值相关的标签。
- 数值标签的例子如:预测一套二手房的售价。
- 类别标签的例子:将图片分类为「苹果」或「橘子」;
监督学习的目的是通过学习许多有标签的样本,然后对新的数据做出预测。例如,预测二手房的售价(回归)或者准确识别新照片上的水果(分类)。
(3-2)无监督学习(Unsupervised learning)一般为“聚类”
通过学习大量的无标记数据,去分析出数据本身的内在特点和结构。
比如:基于大量用户购物的历史记录信息,从数据中去分析用户的不同类别。针对这个问题,最终能划分为几个类别?每个类别有那些特点?我们事先是不知道的,这称为“聚类”(Clustering)。
(3-3)有监督学习和无监督学习中“分类”和“聚类”的区别
- 有监督学习中的“分类”:是我们已经知道了有哪几种类别;
- 分类问题是在已知答案中选择一个
- 无监督学习中的“聚类”:是我们在分析数据之前其实是不知道有哪些类别的。
- 聚类的答案是未知的,需要利用算法从数据里挖掘出数据的特点和结构。
(4)机器学习应用开发的典型步骤
- 数据采集与标记
- 数据清洗
- 特征选择
- 模型选择
- 模型训练和测试
- 模型性能评估和优化
- 模型使用
(5)“欠拟合”+“过拟合” ===>“交叉验证”
- 泛化能力针对的其实是学习方法,它用于衡量该学习方法学习到的模型在整个样本空间上的表现。
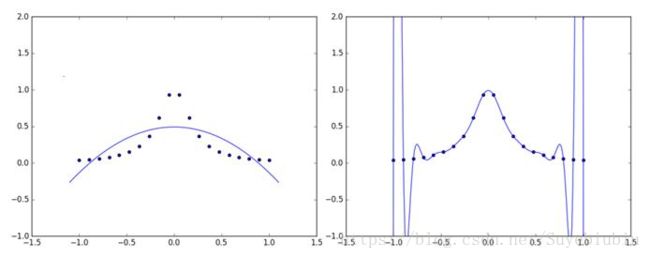
这一点当然是十分重要的,因为我们拿来训练模型的数据终究只是样本空间的一个很小的采样,如果只是过分专注于它们,就会出现所谓的“过拟合”(Over Fitting)的情况。当然,如果过分罔顾训练数据,又会出现“欠拟合”(Under Fitting)。可以用一张图来直观地感受过拟合和欠拟合(如图1所示,左为欠拟合,右为过拟合)。
所以需要“张弛有度”,找到最好的那个平衡点。统计学习中的结构风险最小化(Structural Risk Minimization,SRM)就是研究这个的,它和传统的经验风险最小化(Empirical Risk Minimization,ERM)相比,注重于对风险上界的最小化,而不是单纯地使经验风险最小化。它有一个原则:在使风险上界最小的函数子集中挑选出使经验风险最小的函数。而这个函数子集,正是我们之前提到过的假设空间。
相比起通过选取合适的假设空间来规避过拟合,进行交叉验证(Cross Validation)则可以让我们知道过拟合的程度,从而帮助我们选择合适的模型。常见的交叉验证有以下三种。
- S-fold Cross Validation:中文可翻译成S折交叉验证,它是应用最多的一种方法,其方法大致如下。
- 将数据分成S份:D={D_1,D_2,…,D_S},一共做S次试验。
- 在第i次试验中,使用D-D_i作为训练集,D_i作为测试集对模型进行训练和评测。
- 最终选择平均测试误差最小的模型。
- 留一交叉验证(Leave-one-out Cross Validation):这是S折交叉验证的特殊情况,此时S=N。
- 简易交叉验证:这种实现起来最简单,也是本书(在进行交叉验证时)所采用的方法。它简单地将数据进行随机分组,最后达到训练集约占原数据70%的程度(这个比例可以视情况改变),选择模型时使用测试误差作为标准。
1.2使用Python进行机器学习
- 使用Anaconda
1.3第一个机器学习样例
该问题来自Coursera上的斯坦福大学机器学习课程,其叙述如下:现有47个房子的面积和价格,需要建立一个模型对新的房价进行预测。稍微翻译问题,可以得知:
- 输入数据只有一维,亦即房子的面积。
- 目标数据也只有一维,亦即房子的价格。
- 则根据已知的房子的面积和价格的关系进行机器学习。
(1)获取与处理数据
数据网址:https://github.com/carefree0910/MachineLearning/blob/master/_Data/prices.txt
一般而言,对数据做简单的处理以期望降低问题的复杂度。在这个例子里,采取常用的将输入数据标准化的做法,其数学公式为:
import numpy as np
import matplotlib.pyplot as plt
x,y=[],[] # 定义存储输入数据(x)和目标数据(y)的数组
infos=open('prices.txt','r')
for sample in infos: # 遍历数据集,变量sample对应的正是一个个样本
_x=sample.strip('\n').split(',')[0]
_y=sample.strip('\n').split(',')[1]
x.append(float(_x))
y.append(float(_y)) # 将字符串数据转化为浮点数
x,y=np.array(x),np.array(y) #读取完数据后,将它们转化为Numpy数组以方便进一步的处理
x=(x-x.mean())/x.std() #标准化
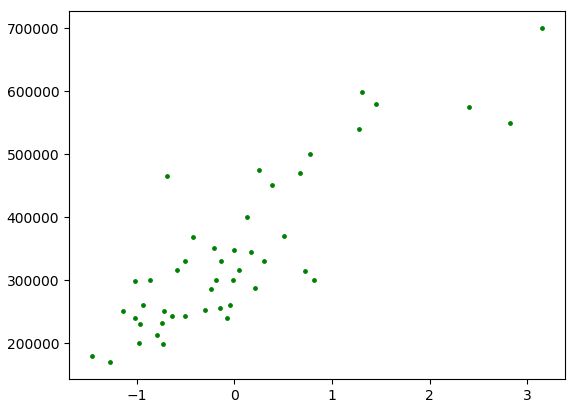
#将原始数据以散点图的形式画出
plt.figure()
plt.scatter(x,y,c='g',s=6)
plt.show()
该图的横轴是标准化后的房子面积,纵轴是房子价格。【此时算是完成机器学习的第一步:数据预处理】
(2)选择与训练模型
通过可视化原始数据,可以非常直观地感受到:很有可能通过线性回归(Linear Regression)中的多项式拟合来得到一个不错的结果。
注意:用多项式拟合散点只是线性回归的很小的一部分,但是它的直观意义比较明显。考虑到问题比较简单,我们才选用了多项式拟合。【此处只是简单使用】
- 其中f(x|p;n)就是我们的模型,p、n都是模型的参数,其中p是多项式f的各个系数,n是多项式的次数。
- L(p;n)则是模型的损失函数, 即欧氏距离(或说向量的二范数)。
- x、y则分别是输入向量和目标向量;在我们这个样例中,x、y这两个向量都是47维的向量,分别由47个不同的房子面积、房子价格所构成。
在确定好模型后,就可以开始编写代码来进行训练了。对于大多数机器学习算法,所谓的训练正是最小化某个损失函数的过程,这个多项式拟合的模型也不例外:我们的目的就是让上面定义的L(p;n)最小。
x0=np.linspace(-2,4,100) # 在(-2,4)这个区间上取100个点作为画图的基础
# 利用Numpy的函数定义训练并返回多项式回归模型的函数
# deg参数代表着模型参数中的n,亦即模型中多项式的次数
# 返回的模型能够根据输入的x(默认是x0),返回相对应的预测的y
def get_model(deg):
return lambda input_x=x0:np.polyval(np.polyfit(x,y,deg),input_x)
Numpy里面带的两个函数:polyfit和polyval的用法。
- polyfit(x, y, deg):该函数会返回使得上述(注:该公式中的x和y就是输入的x和y)最小的参数p,亦即多项式的各项系数。换句话说,该函数就是模型的训练函数。
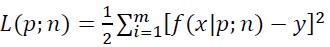
- polyval(p, x):根据多项式的各项系数p和多项式中x的值,返回多项式的值y。
(3)评估与可视化结果
- 模型做好后,我们就要尝试判断各种参数下模型的好坏了。
- 为简洁起见,我们采用n=1,4,10这三组参数进行评估。
- 由于我们训练的目的是最小化损失函数,所以用损失函数来衡量模型的好坏似乎是一个合理的做法。
# 根据参数n、输入的x、y返回相对应的损失
def get_cost(deg,input_x,input_y):
return 0.5*((get_model(deg)(input_x)-input_y)**2).sum()
test_set=(1,4,10)# 定义测试参数集并根据它进行各种实验
for d in test_set:
print('test_set:{}--->{}'.format(d,get_cost(d,x,y))) # 输出相应的损失
"""
test_set:1--->96732238800.35292
test_set:4--->94112406641.67743
test_set:10--->75874846680.09283
"""
那么,怎么最直观地了解是否出现过拟合了呢?当然还是画图了。
#画出相应的图像
plt.scatter(x,y,c="g",s=20)
for d in test_set:
plt.plot(x0,get_model(d)(),label='degree={}'.format(d))
plt.xlim(-2,4)
plt.ylim(1e5,8e5) # 将横轴、纵轴的范围分别限制在(-2,4)、(1×〖10〗^5,8×〖10〗^5)
plt.legend() # 调用legend方法使曲线对应的label正确显示
plt.show()
所得的结果是:
- 当n=1,4,10时,损失的头两位数字分别为96、94和75。这么看来似乎是n=10优于n=4,而n=1最差,
- 但从图可以看出,三条线分别代表n=1、n=4、n=10的情况。可以看出,从n=4开始模型就已经开始出现过拟合现象了,到n=10时模型已经变得非常不合理。似乎直接选择n=1作为模型的参数才是最好的选择。
这里矛盾的来源正是前文所提到过的过拟合情况。
【注:该例子结束。因为数据集太少,所以没有进行交叉验证。】