我用Python做设计(一)
我用Python做设计(一)
目录
- 我用Python做设计一
-
- 目录
- 前言
- 简介
- 数据处理
- 算法分析
-
前言
“铃铃铃,铃铃铃。。。”随着一阵急促的电话,我知道又要有的忙了。“XX,有一份规划,着急要,要求和资料我已经发你了,你抓紧看一下,有什么问题给我打电话。”
晕,难得的清闲时间,又没了,开始接收文件,看看是啥。原来是一份本地区的配网自动化规划设计要求。
简介
看了下要求,原来对本地的配网自动化光纤建设进行规划,做到本地区配网自动化节点和配变节点的光纤100%覆盖。要求知道了,下面就是看看,都有哪些资料。
- 本地的当前配电房的GIS的CAD版本
本地的当前所有配变的Excel版资料
先对本地区的配网自动化组网方案进行一个简要的介绍,本地区的配网光线自动化组网方案,采用以太网交换机的光纤环网的组网方案,环网从变电站出发,串接各个自动化节点,最后再回到变电站。然后原则上,一个变电站可以出不超过4个光纤环,一个环,原则上串接不超过25个节点。
要求有了,先熟悉一下资料,看看有啥可用的。
首先先从CAD中导出所有的变电站资料,看看有多少座变电站,他们都在哪儿。
| 序号 | 变电站 | 坐标X | 坐标Y | 坐标Z |
|---|---|---|---|---|
| 1 | 叶孤城变电站 | 114.0911 | 22.5536 | 0 |
| 2 | 惊云变电站 | 114.1025 | 22.5758 | 0 |
| 3 | 连城变电站 | 114.1035 | 22.5716 | 0 |
| … | … | … | … | … |
| 14 | 香山变电站 | 114.1692 | 22.66 | 0 |
然后是本地的所有配电房的数据,这个数据就比较多了,然后格式也是一样的,就不列举了。
下面开始尝试先对数据有个简单的感受。
数据处理
变电站的数据很少,就先看它。下面,当然是掏出我的大蟒蛇,嘻嘻嘻嘻,将数据处理之后,放进去,代码很简单。
import geoplotlib
from geoplotlib.utils import read_csv, BoundingBox
data = read_csv('data/lh_stations.csv')
geoplotlib.dot(data, point_size=8)
geoplotlib.set_bbox(BoundingBox(22.58, 114.11, 22.53, 114.16))
geoplotlib.show() 得到的效果如下:
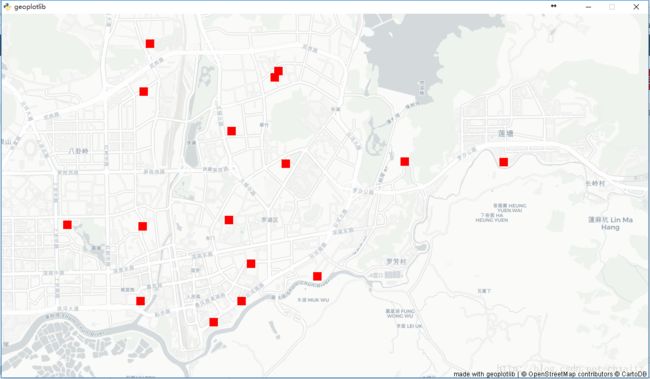
额。。。,好吧,开导自己,我至少知道了这几个变电站在哪儿,看着这些站的位置还是很不平均的,有些地方空出了很大位置,不晓得会不会影响规划。
先不管了,再看看本地区的配电房都在那里吧。配电房数据,肯定不能这么看了,毕竟它要密的多,所以决定用热力图看看,代码也很简单。
import geoplotlib
from geoplotlib.utils import read_csv, BoundingBox
import com
def hist():
data = read_csv('data/lh_powerhouses.csv')
geoplotlib.hist(data, colorscale='sqrt', binsize=16)
geoplotlib.set_bbox(com.boundingBoxDefault)
geoplotlib.show()
hist() 得到的效果如下:
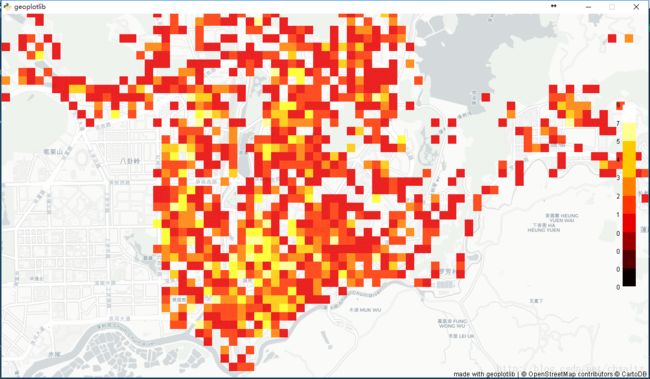
图中,分成若干个矩形区域,然后统计每个矩形区域中的配电房的个数,配电房密度越高,颜色越亮,配电房密度越低,颜色越暗。从中可以看到配电房的分布也是很不均匀的。
粗略的计算了一下,按照业主的要求,1个变电站可以接25*4=100个节点,那14座变电站就可以接1400个节点,对当前的规划来说,是够用的,那下面开始考虑,该怎么能实现业主的要求能。
算法分析
首先想到的就是K-means算法,因为这跟聚类思想很像,假设我如果每个变电站出4个环,然后每个环接不超过25个点的话,通过不断尝试每个分组的最小类,来计算所有的分组。因为,如果要考虑每个环接不超过25个点这个条件的话,算法的复杂度会增大,所以,这里先直接调用经典K-means算法。
K-means算法是硬聚类算法,是典型的基于原型的目标函数聚类方法的代表,它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。
代码比上面的稍长一些。
from geoplotlib.colors import create_set_cmap
import pyglet
from sklearn.cluster import KMeans
import geoplotlib
from geoplotlib.layers import BaseLayer
from geoplotlib.core import BatchPainter
from geoplotlib.utils import BoundingBox
import numpy as np
import com
class KMeansLayer(BaseLayer):
def __init__(self, data):
self.data = data
self.k = 56
def invalidate(self, proj):
self.painter = BatchPainter()
x, y = proj.lonlat_to_screen(self.data['lon'], self.data['lat'])
k_means = KMeans(n_clusters=self.k)
k_means.fit(np.vstack([x,y]).T)
labels = k_means.labels_
self.cmap = create_set_cmap(set(labels), 'hsv')
for l in set(labels):
self.painter.set_color(self.cmap[l])
self.painter.convexhull(x[labels == l], y[labels == l])
self.painter.points(x[labels == l], y[labels == l], 2)
def draw(self, proj, mouse_x, mouse_y, ui_manager):
ui_manager.info('Use left and right to increase/decrease the number of clusters. k = %d' % self.k)
self.painter.batch_draw()
def on_key_release(self, key, modifiers):
if key == pyglet.window.key.LEFT:
self.k = max(2,self.k - 1)
return True
elif key == pyglet.window.key.RIGHT:
self.k = self.k + 1
return True
return False
data = geoplotlib.utils.read_csv('data/lh_powerhouses.csv')
geoplotlib.add_layer(KMeansLayer(data))
geoplotlib.set_smoothing(True)
geoplotlib.set_bbox(com.boundingBoxDefault)
geoplotlib.show() 得到的效果如下:
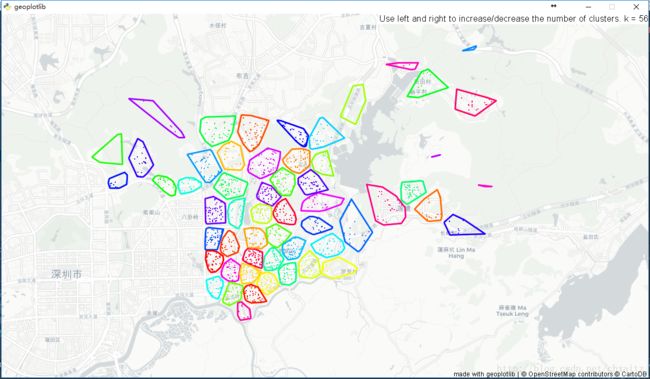
我细数了一下,最多的一个环里面有30+个,所以直接用肯定是不行的。不过暂时看着还像那么回事儿的,把得到的数据,先稍微处理一下,就先这样向老板交差吧,后面再细细考虑算法的问题。( ̄▽ ̄)”