AHP基本思路
AHP通常用于决策判断的重要依据,在某些方面具有很好的指导作用,尤其是定性判断指标转化为定量数据时。比如我们打算新建一座商场,初步认定了A、B、C三地,这三个地区的各项指标都非常接近,此时决策者在做判断时基本就会以拍脑袋为主,这样得出的结论缺乏科学性和说服力,因此这里我们就可以考虑引入AHP来解决这个问题,AHP通过将目标和选择项分别放于最上层和最底层,中间为评价指标,将各指标值按照一定权值加起来得到一个最终的分数,选取分数最大的项为最终结果项,如下图: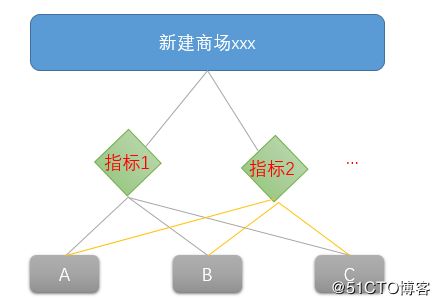
AHP项目应用:
1.介绍完AHP的基本思路后,接下来使用AHP计算用户价值贡献度。
(1)按照用户涉及到的各项业务进行分层,这里我根据项目需要将各项指标分成了三层,第一层为大类指标,主要包含基本属性、行为属性和业务属性,第一层下面为第二层,主要是对第一层的细分,如基本属性下包括信息完整度、认证状况、GPS使用状况等,第三层则为第二层的进一步细分,这类指标通常都为定量数据,或可转化为定量数据的定性数据;
(2)从下往上计算每一层各项指标的权值w,在该项目中只需从第二层开始计算即可;
(3)各层指标值乘以对应权值的累加和即为其大类的值,这一步需要从最底层即第三层开始计算,最后将所有的指标结果加起来便为各个用户的价值贡献度。
2.AHP最核心的部分在于各中间层指标的权值求取,在此过程中其参考了1-9评分规则,将各层间属于同类的指标进行两两比较,由相关的业务人员判断对比的指标哪一项对当前项目结果更重要。
| 指标a | a极度重要 | a非常重要 | a重要 | a稍微重要 | 同等重要 | b极度重要 | b非常重要 | b重要 | b稍微重要 | 指标b |
|---|---|---|---|---|---|---|---|---|---|---|
| 信息完整度 | 1 | 认证状况 | ||||||||
| 信息完整度 | GPS使用 | |||||||||
| 认证状况 | GPS使用 |
业务人员可通过以上表格对指标进行比较,若觉得信息完整度比认证状况重要很多,则可在第一行对应的‘a非常重要’一栏标注为1。
3.将对比结果转化为相应的评分矩阵
def convert_martix(data):
compute_pos = []
pos_to_value = []
data_shape = data.shape
matrix = np.eye(indicates)
#获取对比指标的评分值做在位置
for i in range(data_shape[0]):
for j in range(data_shape[1]):
if data[i][j] == 1:
compute_pos.append([i,j])
pos_shape = np.array(compute_pos).shape
for i in range(pos_shape[0]):
value = 0.0
if compute_pos[i][1] == 1:
value = 9
elif compute_pos[i][1] == 2:
value = 7
elif compute_pos[i][1] == 3:
value = 5
elif compute_pos[i][1] == 4:
value = 3
elif compute_pos[i][1] == 5:
value = 1
elif compute_pos[i][1] == 6:
value = 1.0 / 3
elif compute_pos[i][1] == 7:
value = 1.0 / 5
elif compute_pos[i][1] == 8:
value = 1.0 / 7
elif compute_pos[i][1] == 9:
value = 1.0 / 9
pos_to_value.append(value)
if indicates == 3:
#对称轴上三角
matrix[0][1] = pos_to_value[0]
matrix[0][2] = pos_to_value[1]
matrix[1][2] = pos_to_value[2]
# 对称轴下三角
matrix[1][0] = 1.0 / matrix[0][1]
matrix[2][0] = 1.0 / matrix[0][2]
matrix[2][1] = 1.0 / matrix[1][2]
elif indicates == 4:
matrix[0][1] = pos_to_value[0]
matrix[0][2] = pos_to_value[1]
matrix[0][3] = pos_to_value[2]
matrix[1][2] = pos_to_value[3]
matrix[1][3] = pos_to_value[4]
matrix[2][3] = pos_to_value[5]
matrix[1][0] = 1.0 / matrix[0][1]
matrix[2][0] = 1.0 / matrix[0][2]
matrix[3][0] = 1.0 / matrix[0][3]
matrix[2][1] = 1.0 / matrix[1][2]
matrix[3][1] = 1.0 / matrix[1][3]
matrix[3][2] = 1.0 / matrix[2][3]
elif indicates == 5:
matrix[0][1] = pos_to_value[0]
matrix[0][2] = pos_to_value[1]
matrix[0][3] = pos_to_value[2]
matrix[0][4] = pos_to_value[3]
matrix[1][2] = pos_to_value[4]
matrix[1][3] = pos_to_value[5]
matrix[1][4] = pos_to_value[6]
matrix[2][3] = pos_to_value[7]
matrix[2][4] = pos_to_value[8]
matrix[3][4] = pos_to_value[9]
matrix[1][0] = 1.0 / matrix[0][1]
matrix[2][0] = 1.0 / matrix[0][2]
matrix[3][0] = 1.0 / matrix[0][3]
matrix[4][0] = 1.0 / matrix[0][4]
matrix[2][1] = 1.0 / matrix[1][2]
matrix[3][1] = 1.0 / matrix[1][3]
matrix[4][1] = 1.0 / matrix[1][4]
matrix[3][2] = 1.0 / matrix[2][3]
matrix[4][2] = 1.0 / matrix[2][4]
matrix[4][3] = 1.0 / matrix[3][4]
elif indicates == 6:
matrix[0][1] = pos_to_value[0]
matrix[0][2] = pos_to_value[1]
matrix[0][3] = pos_to_value[2]
matrix[0][4] = pos_to_value[3]
matrix[0][5] = pos_to_value[4]
matrix[1][2] = pos_to_value[5]
matrix[1][3] = pos_to_value[6]
matrix[1][4] = pos_to_value[7]
matrix[1][5] = pos_to_value[8]
matrix[2][3] = pos_to_value[9]
matrix[2][4] = pos_to_value[10]
matrix[2][5] = pos_to_value[11]
matrix[3][4] = pos_to_value[12]
matrix[3][5] = pos_to_value[13]
matrix[4][5] = pos_to_value[14]
matrix[1][0] = 1.0 / matrix[0][1]
matrix[2][0] = 1.0 / matrix[0][2]
matrix[3][0] = 1.0 / matrix[0][3]
matrix[4][0] = 1.0 / matrix[0][4]
matrix[5][0] = 1.0 / matrix[0][5]
matrix[2][1] = 1.0 / matrix[1][2]
matrix[3][1] = 1.0 / matrix[1][3]
matrix[4][1] = 1.0 / matrix[1][4]
matrix[5][1] = 1.0 / matrix[1][5]
matrix[3][2] = 1.0 / matrix[2][3]
matrix[4][2] = 1.0 / matrix[2][4]
matrix[5][2] = 1.0 / matrix[2][5]
matrix[4][3] = 1.0 / matrix[3][4]
matrix[5][3] = 1.0 / matrix[3][5]
matrix[5][4] = 1.0 / matrix[4][5]
return matrix4.对矩阵各纵轴求和
def compute_weight(matrix):
column_sum = []
matrix_shape = matrix.shape
for i in range(matrix_shape[1]):
column_sum.append(matrix[:,i].sum())
return column_sum5.指标权值计算及一致性检验,一致性检验在AHP中具有很重要的地位,它可以矫正业务人员在评分时的随意性,通常要求一致性水平CR小于等于0.1,CR = CI / RI,其中CI = (矩阵特征值 - n) / (n-1) ,n为矩阵中指标个数,RI的值与矩阵阶数有关,参照下表:
RI = {3:0.51, 4:0.89, 5:1.12, 6:1.25, 7:1.35, 8:1.42, 9:1.45, 10:1.49, 11:1.52}
def consis_check(data_arraty,n,ri,guide_line=0.1):
#计算CI及相应权值
x = convert_martix(data_arraty)
y = np.mat(martix_col_sum(x))
c = x / y
w = np.mat(c.sum(axis=1) / n)
CI = (np.dot(y, w) - n) / (n - 1)
CI = CI[0][0]
RI = ri
CR = CI / RI
if CR <= guide_line:
print '一致性检验通过,指标依次权值为:'
print w.T
else:
print '\n*****一致性检验未通过,请重新评估*****'
print CR6.最后上传各指标对比数据,并依序执行上面的函数,可获得对应的指标权值
def data_loads():
columns = ['a','aExtreme','aVery','aImport','aLittle','equal','bLittle','bExtreme','bVery','bImport','b']
data = pd.read_excel('D:\\ahp.xlsx',skiprows=1,names=columns)
indicates = len([x for x in data['a'].append(data['b']).duplicated() if x == False])
print indicates
data_arraty = np.array(data)
return data_arraty,indicates
data_arraty,indicates = data_loads()
consis_check(data_arraty,indicates,RI[indicates])最终得到结果如下:
一致性检验通过,指标依次权值为:
[[ 0.74558145 0.12011708 0.13430147]]