"""
卷积神经网络处理的过程,主要包含4个步骤
1. 图像输入:获取输入的数据图像,一般需要经历float数据类型转换,4维Tensor转换
2. 卷积:对图像特征进行提取
3. maxpool:压缩聚合卷积提取到的特征,起到降维和改善结果的作用
4. 全连接层:用于对图像进行分类
卷积网络在本质上是一种输入到输出的映射,能够学习大量的输入与输出之间的映射关系,而
不需要任何输入与输出之间的精确的数学表达式
在开始训练前,所有的权重都应该用一些不同的小随机数进行初始化。“小随机数”用来保证
网络不会因为权重过大而进入饱和状态,从而导致训练失败。“不同”用来保证网络可以正常地
学习,实际上,如果用相同的数去初始化矩阵,则网络无学习能力
"""
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time
import matplotlib.pyplot as plt
mnist = input_data.read_data_sets("tensorflow_application/MNIST_data/", one_hot=True)
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
print(mnist.train.images.shape)
x_image = tf.reshape(x, [-1, 28, 28, 1])
def weight_variables(shape):
initial = tf.truncated_normal(shape)
return tf.Variable(initial)
def bias_variables(shape):
initial = tf.truncated_normal(shape)
return tf.Variable(initial)
def conv2d(x, w):
return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding="SAME")
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
"""
这里使用的激活函数为sigmoid,传统神经网络中最常用的两个激活函数为sigmoid和tanh, sigmoid
被视为神经网络的核心所在。非线性的sigmoid函数对中央区的信号增益较大,对两侧区的信号增益较小
在信号的特征空间映射上,有很好的效果
sigmoid和tanh激活函数的缺点:左右两端在很大程度上接近极值,容易饱和,使得神经元梯度接近0,这使得
模型在计算时会多次计算接近于0的梯度,导致花费时间而权重又得不到更新
为了克服这一缺点,出现了一种新的函数,ReLU函数
ReLU函数的优点:
1. 收敛快:对于达到阈值的数据其激活力度随着数值的加大而增大,且呈现一个线性关系
2. 计算简单:max(0, x)
3. 不易过拟合:一部分神经元如果在计算时有过大的梯度,则该神经元的梯度将会被强行设置为0,在其后
的训练中处于失活状态,虽然会导致多样化的丢失,但是也能防止过拟合
ReLU的缺点:
不同的学习率对ReLU模型的训练有很大影响,学习率设置不当会造成大量的神经元被锁死
"""
w_conv1 = weight_variables([5, 5, 1, 6])
b_conv1 = bias_variables([6])
conv1 = conv2d(x_image, w_conv1)
h_conv1 = tf.nn.sigmoid(tf.add(conv1, b_conv1))
h_pool1 = max_pool_2x2(h_conv1)
w_conv2 = weight_variables([5, 5, 6, 16])
b_conv2 = bias_variables([16])
conv2 = conv2d(h_pool1, w_conv2)
h_conv2 = tf.nn.sigmoid(tf.add(conv2, b_conv2))
h_pool2 = max_pool_2x2(h_conv2)
w_conv3 = weight_variables([5, 5, 16, 120])
b_conv3 = bias_variables([120])
conv3 = conv2d(h_pool2, w_conv3)
h_conv3 = tf.nn.sigmoid(tf.add(conv3, b_conv3))
w_fc1 = weight_variables([7*7*120, 80])
b_fc1 = bias_variables([80])
h_conv3_flat = tf.reshape(h_conv3, [-1, 7*7*120])
h_fc1 = tf.nn.sigmoid(tf.add(tf.matmul(h_conv3_flat, w_fc1), b_fc1))
w_fc2 = weight_variables([80, 10])
b_fc2 = bias_variables([10])
y_model = tf.nn.softmax(tf.add(tf.matmul(h_fc1, w_fc2), b_fc2))
loss = -tf.reduce_sum(y_ * tf.log(y_model))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
correct_prediction = tf.equal(tf.argmax(y_model, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
train_c = []
test_c = []
sess = tf.InteractiveSession()
init = tf.global_variables_initializer()
sess.run(init)
start_time = time.time()
for i in range(2000):
batch = mnist.train.next_batch(200)
train_step.run(feed_dict={x: batch[0], y_: batch[1]})
if i % 2 == 0:
train_acc = accuracy.eval(feed_dict={x: batch[0], y_: batch[1]})
test_acc = accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels})
train_c.append(train_acc)
test_c.append(test_acc)
print("step %d: \ntraining accuracy %g, testing accuracy %g" % (i, train_acc, test_acc))
end_time = time.time()
print("time: ", (end_time - start_time))
start_time = end_time
sess.close()
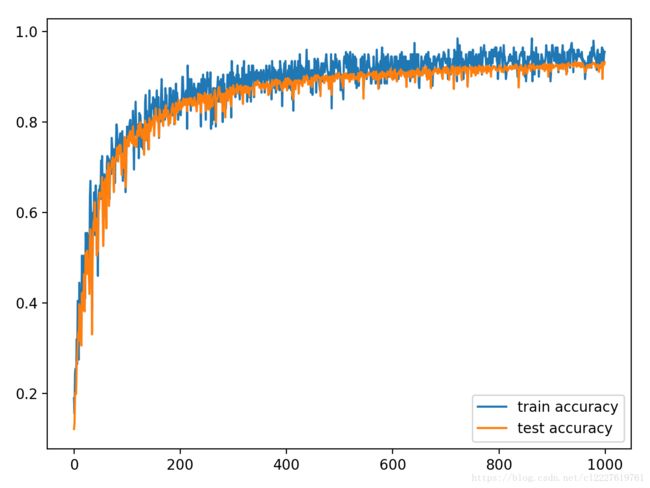
plt.plot(train_c, label="train accuracy")
plt.plot(test_c, label="test accuracy")
plt.legend()
plt.tight_layout()
plt.show()
plt.savefig("tensorflow_application/accu.png", dpi=200)