神经网络

神经网络可以解决当特征太多,计算负荷过大的问题.比如在处理图像问题时,一张图片每一个像素都是一个特征,用神经网络就比较合适.
神经网络起源于80~90年代,但是在90年代后期就减少了.而现在神经网络又再次兴起,原因是计算机运行速度变快,解决了神经网络计算量偏大的问题.
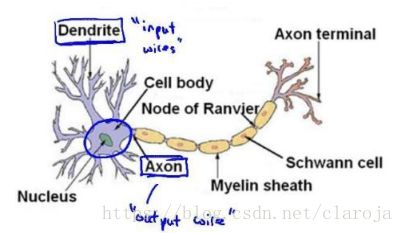
每个神经元都可以被认为是一个处理单元/神经核(processing unit/ Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon)

神经网络模型建立在很多神经元上,每一个神经元又是一个学习模型,也称为激活单元(activation unit),在神经网络中参数 θ θ 由被称为权重(weight).

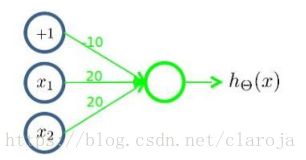
其中 x1,x2,x3 x 1 , x 2 , x 3 是输入单元(input units),这个是原始的特征
a1,a2,a3 a 1 , a 2 , a 3 是中间单元,
最后是输出单元,计算 hθ(x) h θ ( x ) .
每一层的输出变量都是下一层的输入变量.第一城(layer1)是输入层(input layer),最后一层(layer3)称为输出层(output layer),中间一层称为隐藏层(hidden layers).每一层都增加一个偏差单元(bias unit)

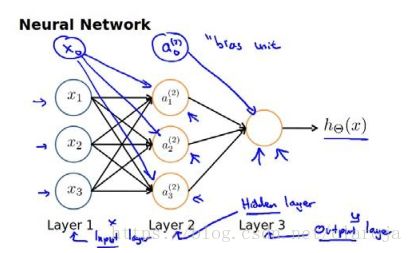
a(j)i a i ( j ) 代表第j层的第i个激活单元.
θ(j) θ ( j ) 代表从第j层映射到第j+1层时的权重的矩阵,例如 θ(1) θ ( 1 ) 代表从第一层映射到第二层的权重的矩阵.其尺寸为以j+1层激活单元数量为行数,以第j层的激活单元数加1为列的矩阵.例如,上图所示矩阵 θ(1) θ ( 1 ) 的尺寸为3*4.
对于上图,激活单元和输出分别是:

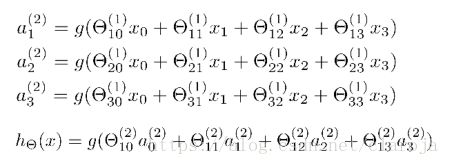
每一个激活单元a都是由上一层所有的x和每一个x所对应的 θ θ 决定的.我们把这样的从左到右的神经网络算法称为前向传播算法(Forward Propagation).

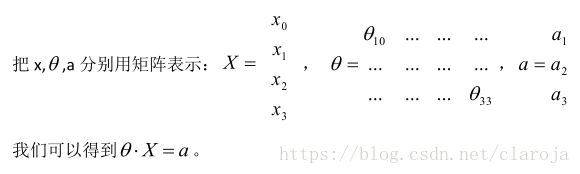
神经网络与逻辑回归

右半部分其实就是以 a0,a1,a2,a3 a 0 , a 1 , a 2 , a 3 按照逻辑回归的方式输出 hθ(x) h θ ( x ) .其实神经网络就像是逻辑回归,只不过我们把逻辑回归的输入向量变成了隐藏层的激活单元的输出结果.
我们可以把 a0,a1,a2,a3 a 0 , a 1 , a 2 , a 3 看成更为高级的特征值,也就是 x0,x1,x2,x3 x 0 , x 1 , x 2 , x 3 的进化体,它是由x与 θ θ 决定的.

直观理解
在逻辑回归中,我们只能使用原始特征 x0,x1,x2,x3 x 0 , x 1 , x 2 , x 3 ,而在神经网络中原始特征只是输入层,最后做预测的是根据隐藏层处理之后的新特征.
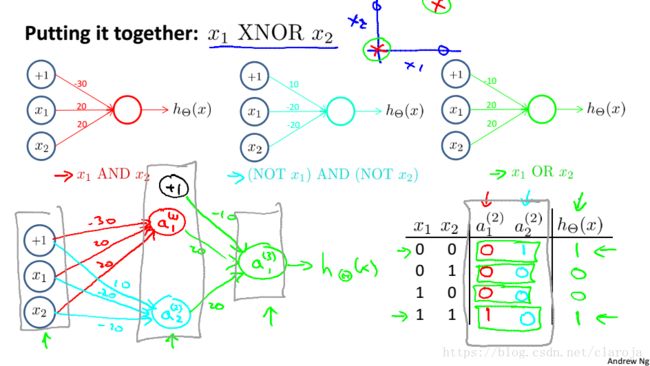
在神经网络中,单层神经网络(无中间层)的计算可用来表示逻辑运算,比如逻辑AND.逻辑OR.
AND

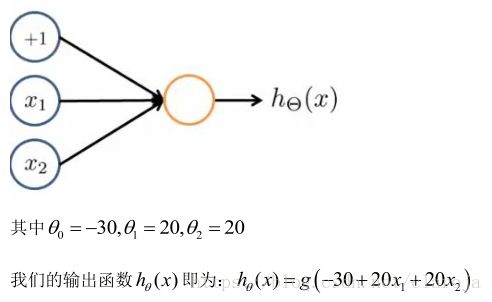
所以 g(x) g ( x ) 的图像是:

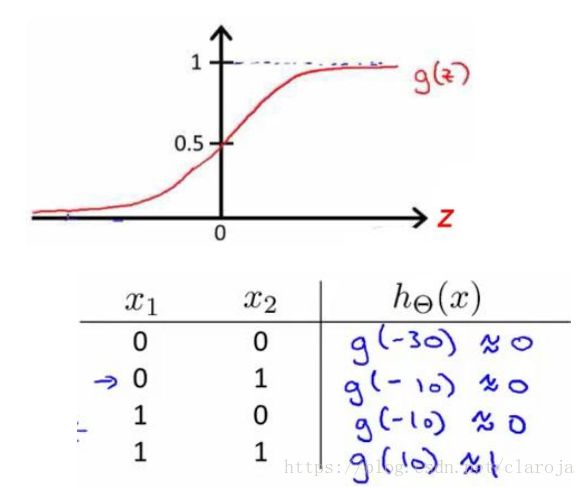
OR

二元逻辑运算符(Binary logical operators)当输入特征为布尔值(0或1)时,我们可以用一个单一测激活层作为二元逻辑运算符,为了表示不同的运算逻辑,只需要选择不同的权重即可.
逻辑与(AND)

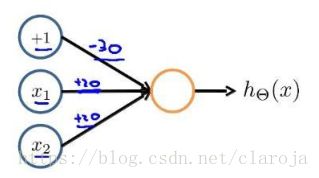
逻辑或(OR)

逻辑非(NOT)

将表示:
AND
(NOT x1 x 1 ) AND(NOT x2 x 2 )
OR的神经元进行组合

综合以上逻辑判断表示XNOR