为传递函数自动设定PID参数——pidtune学习笔记

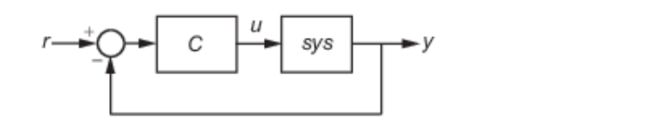
装置模型和PID控制器的基本模型

在命令行里设计PID控制器

装置模型为一个传递函数：
$$sys=\frac{1}{(s+1{)}^3}$$
首先创建一个装置的模型sys，并设计一个简单的PI控制器

sys = zpk([],[-1 -1 -1],1);
% C_pi是一个PI开环控制器
[C_pi,info] = pidtune(sys,'Pi');

此时装置模型和控制器分别为

sys =
     1
  -------
  (s+1)^3
Continuous-time zero/pole/gain model.
    
C_pi = 
             1 
  Kp + Ki * ---
             s 
  with Kp = 1.14, Ki = 0.454
Continuous-time PI controller in parallel form.

接着创建一个反馈控制器，并检查闭环的阶跃相应

% 反馈控制
T_pi = feedback(C_pi*sys, 1);
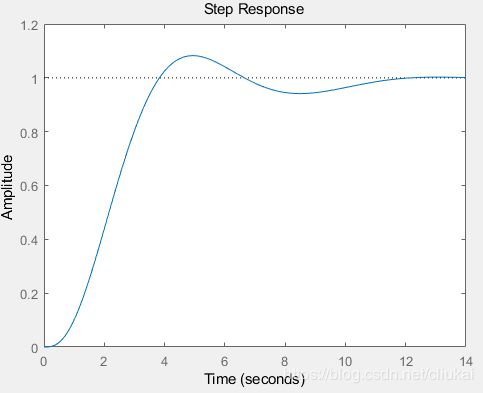
% 画图，显示阶跃相应
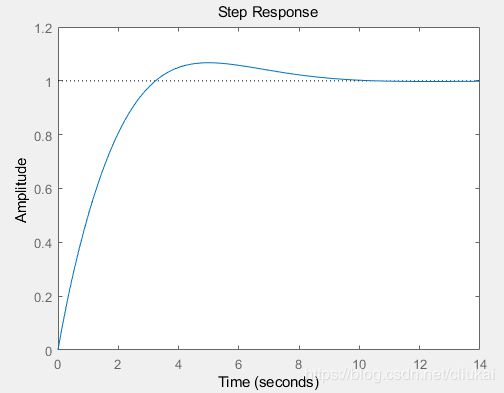
step(T_pi)

得到

将交叉频率设定成1.0

% 提高响应时间
% 设计一个快速反应的PI控制器
[C_pi_fast,info] = pidtune(sys,'Pi',1.0);
T_pi_fast = feedback(C_pi_fast*sys,1);
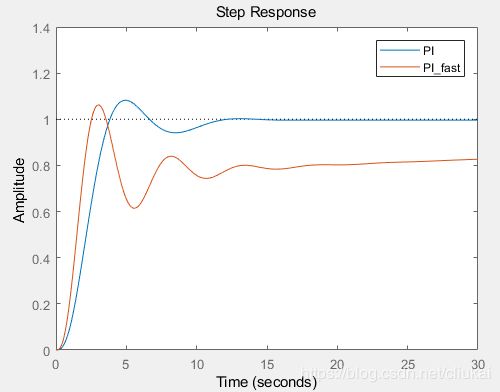
step(T_pi,T_pi_fast)
axis([ 0 30 0 1.4])
legend('PI','PI_fast')

最终发现始终无法达到参考值，因为PI控制器的自由度不够，最后设计一个PIDF控制器

% PIDF控制器
[C_pidf_fast,info] = pidtune(sys,'PIDF',1.0)
T_pidf_fast =  feedback(C_pidf_fast*sys,1);
% 对比PI控制器和PIDF控制器
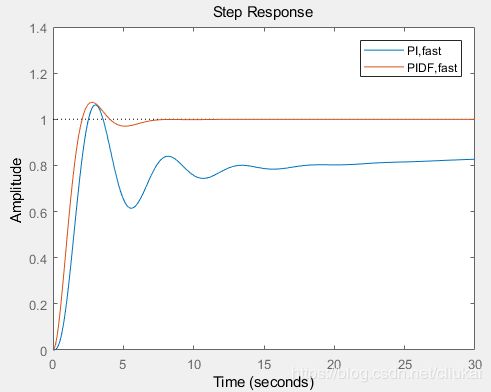
step(T_pi_fast, T_pidf_fast);
axis([0 30 0 1.4]);
legend('PI,fast','PIDF,fast');

设计一个2-DOF二自由度的PID控制器

装置的二阶传递函数模型为：
$$G(s)=\frac{1}{s^2+0.5s+0.1}$$
使用1.5rad/s的带宽：

wc = 1.5;
G = tf(1,[1 0.5 0.1]);
C2 = pidtune(G,'PID2',wc)

或者直接使用PID这样的type模式，例如

传递函数如下：

 G = tf(0.0575,[1 2.4635 0.7980]) Controller_PID = pidtune(G,'PID')

控制器为

Controller_PID =
 
             1          
  Kp + Ki * --- + Kd * s
             s          

  with Kp = 27.7, Ki = 15, Kd = 11.3
 
Continuous-time PID controller in parallel form.

添加闭环控制

Controller_feedback = feedback(Controller_PID*G,1)

Controller_feedback =
 
    0.6471 s^2 + 1.594 s + 0.8617
  ----------------------------------
  s^3 + 3.111 s^2 + 2.392 s + 0.8617
 
Continuous-time transfer function.

% 画图
step(Controller_feedback)