无人驾驶的规划与控制(三)——动作规划(轨迹规划和速度规划)
文章目录
- 1 无人驾驶的动作规划
- 2 轨迹规划
- 2.1 车辆模型
- 2.2 道路定义
- 2.3 候选轨迹生成
- 2.4 根据轨迹点构建有向图并搜索
- 3 速度规划
- 3.1 S-T图算法
- 3.2 设置Cost
1 无人驾驶的动作规划
动作规划的目的:是将上游行为决策(behavior)的宏观指令解释成一条带有时间信息的轨迹曲线(trajectory),最后给底层的反馈控制。
一种简单的思路是,将动作规划问题拆分成两个问题:
- 轨迹规划(Trajectory Planning):二维平面上的优化轨迹问题。
- 速度规划(Speed Planning):选定轨迹后,用什么样的速度行驶这条轨迹。
分开优化不一定能保证总体最优解,但在实际工程实践中,分开优化是更实际有效的解决方案。
2 轨迹规划
2.1 车辆模型
车辆的姿态向量为 x ‾ = ( x , y , θ , κ , υ ) \overline{x}=(x,y,\theta,\kappa,\upsilon) x=(x,y,θ,κ,υ)
| 符号 | 含义 |
|---|---|
| ( x , y ) (x,y) (x,y) | 车辆在二维片面内的位置 |
| θ \theta θ | 车辆的朝向 |
| κ \kappa κ | 曲率,即朝向 θ \theta θ的变化率 |
| υ \upsilon υ | 车辆的速度,即轨迹任意点的切线速度 |
这些姿态变量满足以下关系:
x ˙ = v cos θ y ˙ = v sin θ θ ˙ = v κ \begin{aligned} \dot{x} &=v \cos \theta \\ \dot{y} &=v \sin \theta \\ \dot{\theta} &=v \kappa \end{aligned} x˙y˙θ˙=vcosθ=vsinθ=vκ
轨迹相对于车辆姿态的系统关系为:
d x / d s = cos ( θ ( s ) ) d y / d s = sin ( θ ( s ) ) d θ / d s = κ ( s ) \begin{array}{l}{\mathrm{d} x / \mathrm{d} s=\cos (\theta(s))} \\ {\mathrm{d} y / \mathrm{d} s=\sin (\theta(s))} \\ {\mathrm{d} \theta / \mathrm{d} s=\kappa(s)}\end{array} dx/ds=cos(θ(s))dy/ds=sin(θ(s))dθ/ds=κ(s)
2.2 道路定义
轨迹规划算法非常依赖于地图中对于道路中心线(Center Line)的定义,用一个采样函数去定义道路,采样函数为 r ( s ) = [ r x ( s ) , r y ( s ) , r θ ( s ) , r κ ( s ) ] r(s)=\left[r_{x}(s), r_{y}(s), r_{\theta}(s), r_{\kappa}(s)\right] r(s)=[rx(s),ry(s),rθ(s),rκ(s)],车辆姿态点和道路坐标系以及道路采样函数的关系满足:
x r ( s , l ) = r x ( s ) + l cos ( r θ ( s ) + π / 2 ) y r ( s , l ) = r y ( s ) + l sin ( r θ ( s ) + π / 2 ) θ r ( s , l ) = r θ ( s ) κ r ( s , l ) = ( r κ ( s ) − 1 − l ) − 1 \begin{array}{l}{x_{r}(s, l)=r_{x}(s)+l \cos \left(r_{\theta}(s)+\pi / 2\right)} \\ {y_{r}(s, l)=r_{y}(s)+l \sin \left(r_{\theta}(s)+\pi / 2\right)} \\ {\theta_{r}(s, l)=r_{\theta}(s)} \\ {\kappa_{r}(s, l)=\left(r_{\kappa}(s)^{-1}-l\right)^{-1}}\end{array} xr(s,l)=rx(s)+lcos(rθ(s)+π/2)yr(s,l)=ry(s)+lsin(rθ(s)+π/2)θr(s,l)=rθ(s)κr(s,l)=(rκ(s)−1−l)−1
| 符号 | 含义 |
|---|---|
| s s s | 纵向位移,道路中心线切线方向位移 |
| l l l | 横向位移 |
假设对于某条道路Lane(k),纵向宽度 l k l_k lk不变。那么该道路可以标示为一个随着中心线横向位移的点集 { p ( s , l k ) : s ∈ R + } \left\{p\left(s, l_{k}\right) : s \in \boldsymbol{R}^{+}\right\} {p(s,lk):s∈R+},这样的一个坐标系统为SL坐标系统。
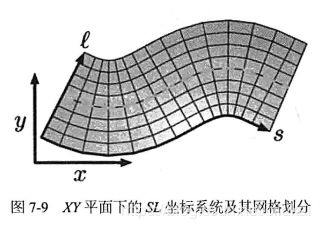
2.3 候选轨迹生成
首先,定义车辆的轨迹(Trajectory)为一个从[0,1]区间到车辆姿态向量集合 C = { x ⃗ } C=\{\vec{x}\} C={x}的连续映射: ρ : [ 0 , 1 ] → C \rho :[0,1] \rightarrow C ρ:[0,1]→C,或者理解为一系列车辆姿态的序列。
| 符号 | 含义 |
|---|---|
| ρ 1 ( 0 ) \rho_{1}(0) ρ1(0) | 第一条道路的起点姿态 |
| ρ 1 ( 1 ) \rho_{1}(1) ρ1(1) | 第一条道路的终点姿态 |
| q init q_{\text {init}} qinit | 广义上的,初始姿态向量, q init = ( x I , y I , θ l , κ l ) q_{\text { init }}=\left(x_{I}, y_{I}, \theta_{l}, \kappa_{l}\right) q init =(xI,yI,θl,κl) |
| q e n d q_{\mathrm{ end}} qend | 广义上的,目标姿态向量, q g o a l = ( x G , y G , θ G , k G ) q_{\mathrm{goal}}=\left(x_{G}, y_{G}, \theta_{G}, k_{G}\right) qgoal=(xG,yG,θG,kG) |
轨迹优化的目标,就是在所有可能轨迹中,筛选出满足边界条件的轨迹曲线,再寻找一条最平滑,Cost最低的曲线。候选轨迹曲线用类似路由寻径模块中的“撒点”采样生成,这样,一条轨迹就可以看成是沿着Lane的中心线纵向位移方向,连接不同Trajectory Point的平滑曲线。
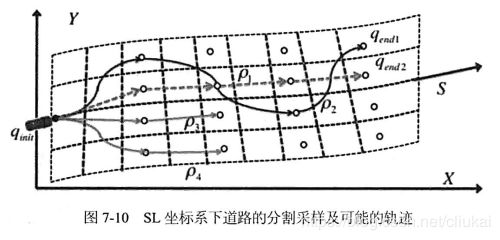
这里,采用多项式螺旋线连接轨迹点,生成候选曲线。多项式螺旋线,代表了一类曲率用弧长(对应这里的s)多项式函数来表示的曲线簇。一般使用三阶或者五阶多项式螺旋线,曲率 κ \kappa κ和轨迹弧长 s s s的关系为:
三 阶 : k ( s ) = k 0 + k 1 s + k 2 s 2 + k 3 s 3 三阶:k(s)=k_{0}+k_{1} s+k_{2} s^{2}+k_{3} s^{3} 三阶:k(s)=k0+k1s+k2s2+k3s3
五 阶 : k ( s ) = k 0 + k 1 s + k 2 s 2 + k 3 s 3 + k 4 s 4 + k 5 s 5 五阶:k(s)=k_{0}+k_{1} s+k_{2} s^{2}+k_{3} s^{3}+k_{4} s^{4}+k_{5} s^{5} 五阶:k(s)=k0+k1s+k2s2+k3s3+k4s4+k5s5
三阶和五阶的区别为:三阶多项式会导致曲率的二阶导数 d κ 2 / d s 2 \mathrm{d} \kappa^{2} / \mathrm{d} s^{2} dκ2/ds2(对应方向盘转速)不连续,而五阶可以同事保持曲率的一阶导数和二阶导数的连续性。
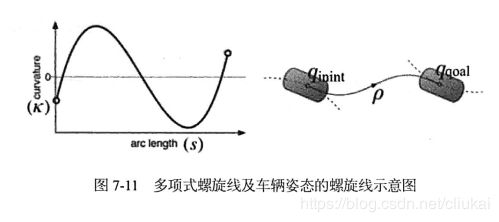
最后,最优利用梯度下降方法搜索,得到三阶(五阶)螺旋线连接的轨迹。
2.4 根据轨迹点构建有向图并搜索
在车辆模型,道路模型,轨迹点模型,和多项式螺旋曲线的设定下,轨迹规划问题可以简化为: ∣ l total / Δ l ∣ × ∣ s total / Δ s ∣ \left|l_{\text { total }} / \Delta l\right| \times\left|s_{\text { total }} / \Delta s\right| ∣l total /Δl∣×∣s total /Δs∣个轨迹点连接成的 ∣ l total / Δ l ∣ ∣ s ual / Δ r ∣ \left|l_{\text { total }} / \Delta l\right|^{\left|s_{\text { ual }} / \Delta r\right|} ∣l total /Δl∣∣s ual /Δr∣条候选曲线的搜索问题。
所有的轨迹点构成了一个图 G = ( V , E ) G=(V, E) G=(V,E)。
| 符号 | 含义 |
|---|---|
| l t o t a l l_{total} ltotal | 道路总宽度 |
| Δ l \Delta l Δl | 宽度的最小采样长度 |
| s t o t a l s_{total} stotal | 道路总长度 |
| Δ s \Delta s Δs | 长度的最小采样长度 |
| V V V | 轨迹点, v ∈ V , v = ( x , y , s , l ) v \in V, v=(x, y, s, l) v∈V,v=(x,y,s,l) |
| E E E | 三阶(五阶)多项式螺旋曲线 |
3 速度规划
3.1 S-T图算法
速度规划的任务,是在动作规划的轨迹上,考虑下游执行限制和行为决策结果,在每个轨迹点上,加入速度和加速度信息。
速度规划主要考虑对动态障碍物的规避,这里引入S-T(纵向位移 - 时间)的概念,并把无人车的速度规划问题,抽象到在S-T图上搜索的问题进行求解。
任何一个S-T图都基于一条已经给定的轨迹曲线,根据预测模块对动态障碍物的轨迹预测,每个动态障碍物都会在这条给定的轨迹上有所投影,从而产生一定S-T区域的覆盖,这里举一个S-T图速度优化算法的例子。
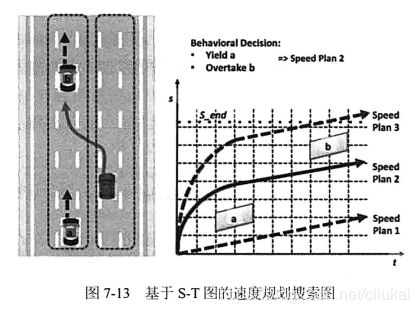
图中,无人车正在思考轨迹规划要选取的换道轨迹,目标车道有前车b,后车a,则a和b在轨迹上的投影就是平行于s轴的线段,随着t的增加,这个投影平行四边形也会不断向右延伸。
模仿轨迹规划的地图划分,把地图分成小网格(Lattice Grid),对每个网格赋予Cost,最终速度规划问题就可以归纳为:从起点 ( s = 0 , t = 0 ) (s=0,t=0) (s=0,t=0)到终点 ( s = S e n d , t > 0 ) (s=S_{end},t>0) (s=Send,t>0)在网格上寻找最小路径Cost的搜索问题。
图中3种方案分别为:
| 方案 | 说明 |
|---|---|
| Speed Plan 3 | 加速直接超过a和b |
| Speed Plan 2 | 超过a(Overtake),然后让b先过(Yield) |
| Speed Plan 1 | 让车a和b,一直跟在后面 |
3.2 设置Cost
根据决策信息,可以灵活调整障碍物周边的Cost,来达到速度调整的目的。例如,
上游决定对a超车,就在S-T图上将a运动轨迹上方网格的Cost调小;
上游决定对b让车,就在S-T图上将b运动轨迹下方网格的Cost调小;
为了避免碰撞,所有动态障碍物轨迹经过的网格Cost都需要调大。
因此,设置Cost是速度规划中S-T图算法的关键,在这个基础上,利用A*或者Dijkstra搜索算法,就能得到最小Cost轨迹。在得到了轨迹之后,通过计算任意轨迹点处的一阶导数和二阶倒数,就能计算出速度和加速度,从而完成速度规划的计算。
参考文章
《第一本无人驾驶技术书》刘少山
在Typora中输入公式
Typora开启行内公式
常用数学符号的 LaTeX 表示方法
一份不太简短的LATEX2ε介绍【精华】