后缀自动机的构造
后缀自动机的构造
最近看了一些后缀自动机的论文,对于后缀自动机的构造过程有了些许了解。
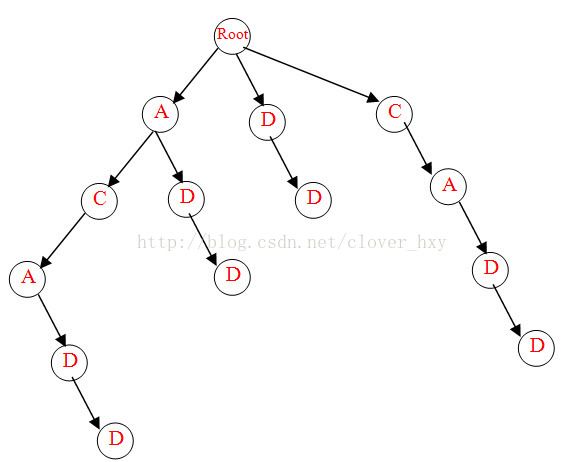
首先后缀自动机顾名思义就是一颗包含了原串s所有后缀的字母树。如果直接像构建trie树的方式构建节点数应该是|S|^2,这个空间显然承受不住。
观察上图可以发现有很多的节点都只有一个儿子,并且相同的部分非常多,所以后缀自动机就是用增量法进行构造,使最终的状态数变成|s|。在后缀自动机中每个节点可能会代表多个状态(也就是一个节点会成为多个节点的儿子),这样节省了空间并且保证自动机中包含了原串的所有子串。
先讲讲后缀自动机的大致做法:假设当前已经建好了s的某个前缀的后缀自动机t,那么就要通过某种算法,添加一个字符x,得到s另一前缀tx的后缀自动机,这样每次插入一个字符,最后把s的所有字符按顺序插入完毕就得到了s的后缀自动机.
这样的话,建造后缀自动机的过程是在线的,就是说,询问s的某些信息,也可以任意时刻在s的结尾插入一些字符,变成新的字符串.不过,删除是不支持的.
先引进一些定义:ch[x][s]表示的是节点x(也可以说是状态)字符s的节点编号。返回该结点对应的子串加上某个字符后生成的合法子串在后缀自动机中所对应的位置(其实就和字母树一样),如果该指针不存在,就说明这样的子串是不存在的(即不是s的子串)
fa[x]其实就是parent指针,但是注意这里的fa[x]表示的并不是他的父亲是谁,因为上面也说过了一个节点因为代表了多个含义所以他也有多个父亲。所以parent指针指向的位置表示的是如果当前节点可以接某个后缀那么parent指针指向的节点也一定可以接。即上一个可以接受后缀的节点。
right(s)表示的子串s在原串中所有出现位置的右端点的集合。对于right满足right(s)是right(fa(s))的子集。right的求法,按照parent树中深度从大到小,依次将每个状态的right集合并入他fa状态的right集合。
l[x]表示的是从根节点到该节点的最大距离,对于一个状态s,他代表的串的长度区间就是(len[fa],len[x]].
再引进一些不错的性质:
①从root到任意结点p的每条路径上的字符组成的字符串,都是当前串t的子串.
②因为满足性质一,所以如果当前结点p是可以接收新后缀的结点,那么从root到任意结点p的每条路径上的字符组成的字符串,都是必定是当前串t的后缀.
③如果结点p可以接收新的后缀,那么p的fa指向的结点也可以接收后缀,反过来就不行.
构造方法增量法:
增量法。我们对于每个状态s,记他代表的最长子串的长度为l(就是上面提到的l[x])
考虑我们当前已经有了前}s|-1个字符的后缀自动机,且现在的自动机中[1,|s|-1]处于end状态(就是终结状态)
现在加入第|s|个字符(设为c),我们令新建了的状态为np,显然l[np]=|s|
然后考虑如何转移:我们加入的是一个last->np的转移,我们也应该加入一个fa(last)->np的转移,直到我们发现到达某个状态已经有一个字符c的转移为止。不妨设这个状态是p,设他经过字符c的转移后的状态为q
如果最终到达root,那么直接将fa[np]=root
如果不为根节点root,就分以下两种情况讨论。
1.len[q]=len[p]+1.这就是说明p,q直接相连中间不夹杂其他的字符,那么q代表的所有串的right集合相同,那我们我们将fa[np]=q即刻。为什么要这么做呢?这样是可以节省空间和状态的,这么连接之后q点就代表了他之前的状态以及现在新加入的状态。
2.len[q]>len[p]+1.这种情况下q代表的串总,长度不超过len[p]+1的串的right集合会多出一个值{s|,而长度超过它的串这不会,之所以会出现len[q]>len[p]+1的情况就是因为p,q之间可能还存在其他的字符,而我们先加入的状态是不满足的。那么为了维护一个状态中所有串的right相同这一性质,我们需要新建了一个状态nq,nq代表的是原来q代表的串中所有长度不超过len[p]+1的串,因此len[nq]=len[p]+1,nq的其他属性(fa和转移)和原来的q点一致,同时建立新的fa指针fa[q]=fa[np]=nq,也就是用nq代表了q,np两个状态。
然后我们再次从p开始:本来p的c字符转移到的点是q,现在它转移到nq。同理fa[q]的c字符也要转移到nq,直到当前点的c字符转移到的不是q为止。
下面以ACADD为例的后缀自动机的构造过程。(实边指的是ch[x][s]指针,虚边是fa指针)
我比较懒所以图片是下载的别人的。。。
1.加入节点A
2.加入节点C
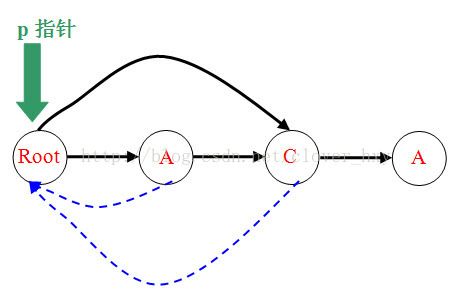
3.加入节点A
fa[last]的字符A已经有转移了,发现此时len[q]=len[p]+1,q表示的right集合都相同,所以我们直接将fa指针指向q即可,此刻开始root的A儿子现在有双重身份(后缀“A”的最后一个字符,和后缀”ACA”的最后一个字符),而且因为第一个A对于root来说,代替了第二个A,所以root不用往第二个A结点连边。
4.加入节点D
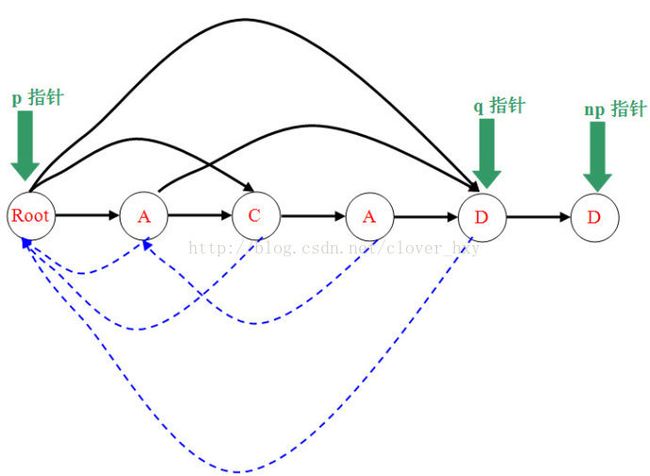
5.加入第二个节点D
我们发现fa[last]的字符D已经有转移了,并且len[q]>len[q]+1,那么我们无法用q来代替,需要新建nq,并更改一系列的关系。
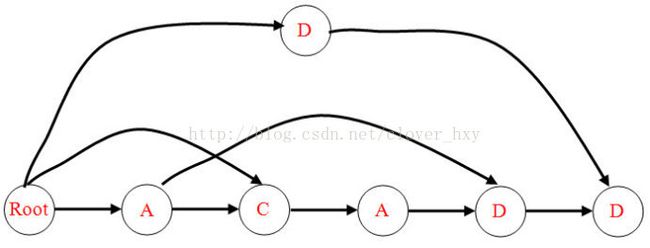
最后后缀自动机就建成了。遍历下图就可以得到原串的所有子串。