省队集训Round2 DAY1
T1
题解
对于每个位置都可以暴力的找到最右边的一个点使之后的点再异或异或和下降。
可以维护一颗主席树,外层表示的是起点,内层表示的是以该点为起点的所以终点的合法区间。
每次利用前缀和作差即可。因为是区间操作所以我们标记永久化一下。
代码
#include" "<<pos<1],1,n,i,pos);
}
scanf("%d",&m);
int ans=0;
for (int i=1;i<=m;i++) {
int l,r; scanf("%d%d",&l,&r);
l=(l+ans)%n+1; r=(r+ans)%n+1;
// cout<" "<if (l>r) swap(l,r);
ans=qjchange(root[r],root[l-1],1,n,l,r,0);
printf("%d\n",ans);
}
} T2
题解
从高的开始消,消到左右两边较高的位置,然后把他们合并成一大列一起向下消。
关键就是怎么划分,对于每一大列维护del[i]表示的是如果当前阶段继续向下消,上面还有多少空可以补。
代码
#includelong long,int> > p;
LL k,f[N],h[N],del[N]; int n,l[N],r[N],fa[N];
int find(int x)
{
if (fa[x]==x) return x;
fa[x]=find(fa[x]);
return fa[x];
}
int main()
{
freopen("a.in","r",stdin);
scanf("%d%lld",&n,&k);
for (int i=1;i<=n;i++) scanf("%lld",&h[i]);
for (int i=1;i<=n;i++) {
p.insert(make_pair(h[i],i));
l[i]=r[i]=fa[i]=i;
}
LL ans=0;
while (p.size()) {
int x=(*--p.end()).second;
p.erase(--p.end());
LL L=l[x]-1==0?0:h[find(l[x]-1)];
LL R=r[x]+1==n+1?0:h[find(r[x]+1)];
LL hi=max(L,R);
LL sum=(LL)(r[x]-l[x]+1)*(h[x]-hi);
if (del[x]>=sum) del[x]-=sum;
else sum-=del[x],ans+=(sum-1)/k+1,del[x]=(k-sum%k)%k;
h[x]=hi;
if (hi!=0) {
if (L==hi) {
int t=find(l[x]-1);
del[x]+=del[t];
p.erase(make_pair(L,t));
fa[t]=x; l[x]=l[t];
}
if (R==hi) {
int t=find(r[x]+1);
del[x]+=del[t];
p.erase(make_pair(R,t));
fa[t]=x; r[x]=r[t];
}
p.insert(make_pair(h[x],x));
}
}
printf("%lld\n",ans);
}T3
题解
首先需要知道斐波那契数列的一个性质
gcd(f[a],f[b])=f[gcd(a,b)]
这个怎么证明?先证明 gcd(f[a],f[a+1])=1
f[0]=1,f[1]=1,gcd(f[0],f[1])=1
利用更相减损, gcd(f[a],f[a+1])=gcd(f[a],f[a]+f[a−1])=gcd(f[a],f[a−1]) ,最终得到 gcd(f[a],f[a+1])=gcd(f[0],f[1])
还需要用到一个式子
f[n+m]=f[n+1]f[m]+f[n]f[m−1]
这道题有一种有趣的组合的证明方法(摘自小火车的论文)
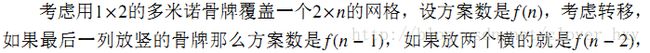
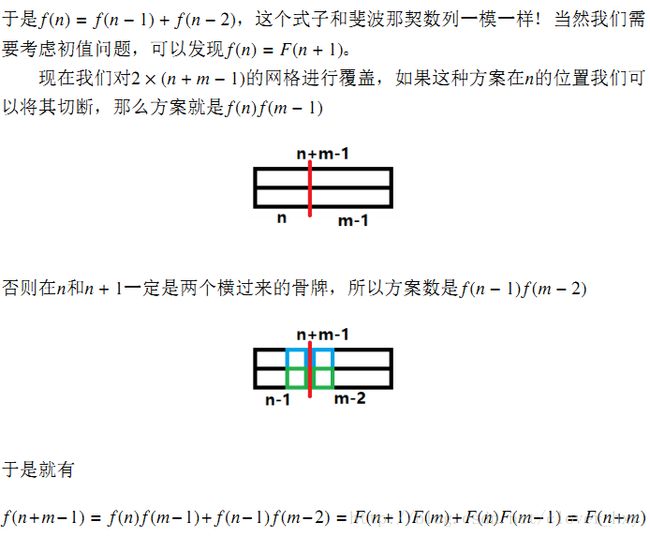
gcd(f[a],f[b])=gcd(f[a],f[a]f[b−a+1]+f[a−1]f[b−a])=gcd(f[a],f[a−1]f[b−a])
因为 gcd(f[a],f[a−1])=1 ,那么 gcd(f[a],f[b])=gcd(f[a],f[b−a]) ,可以递归,就是辗转相除嘛。那么上面的问题得证。
lcm(f[a],f[b])=f[a]f[b]f[gcd(a,b)]
设读入的下标构成的集合为 S ,那么
lcm=∏T∈S,T≠∅f[gcd(T)](−1)|T|−1,其中gcd(T)表示的是集合T中所有数的最大公约数
然后考虑枚举 gcd(T)=i
lcm=∏i=1maxf[i]∑T∈S,T≠∅,gcd(T)=i(−1)|T|−1
式子的瓶颈在于 gcd(T)=i ,我们可以利用莫比乌斯反演进行转化。
设 g(i)=∑T∈S,T≠∅,gcd(T)=i(−1)|T|−1,h(i)=∑T∈S,T≠∅,i|gcd(T)(−1)|T|−1
T≠∅ 比较讨厌,我们发现空集比较讨厌,考虑直接提出来。然后再把指数中的 −1 提出来,式子可以化简成
h(i)=1−∑T∈S,i|gcd(T)(−1)|T|
∑T∈S,i|gcd(T)(−1)|T|=∑|S|i=0(−1)i∗C(|S|,i),C表示组合数
其实就是杨辉三角中某一行的偶数列的和-奇数列的和,在 |S|>0 是式子的值恒等于0
所以
h(i)=[下标中会否有i的倍数]
根据莫比乌斯反演
g(n)=∑d|nh(d)∗μ(dn)
那么 lcm=∏i=1maxf[i]g[i] 可以用 O(nlogn) 的时间预处理 g[i] 数组,然后再用快速幂求解。
代码
#include



