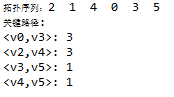关键路径算法 Java实现
如果要对一个流程图活的最短时间,就必须分析他们的拓扑关系,并且找到当中最关键的流程,
这个流程的时间就是最短时间
AOE网(Activity On Edge Network):
* 在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间。
* 注:与AOV网不同的是,AOV网是顶点表示活动的网,它值描述活动之间的制约关系,而AOE网是用边表示活动的网,边上的权值表示活动持续的时间。
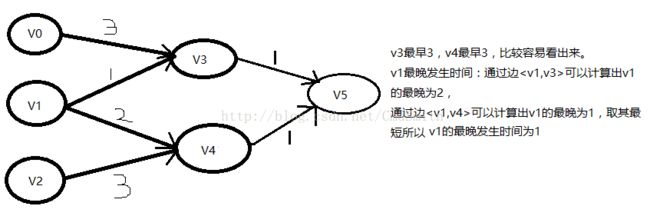
结合 图1中的v3,v4理解事件的最早发生时间,v1理解事件的最晚发生时间比较好。
代码中的图
图1:
图1中事件的最早和最晚发生时间
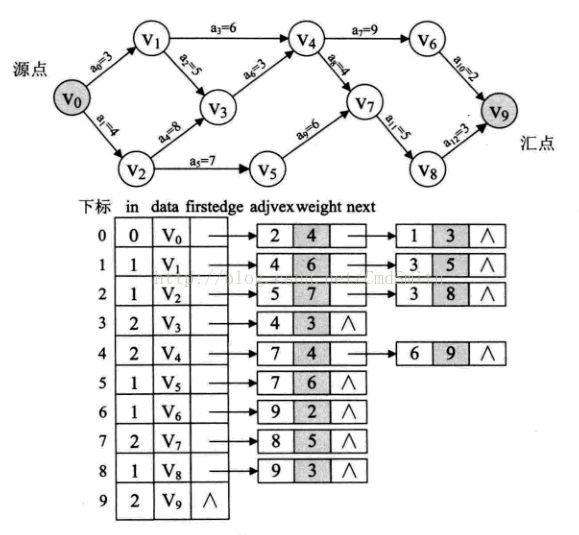
图2:
图2中事件的最早和最晚发生时间
代码:
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/**
* AOE网(Activity On Edge Network):
* 在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间。
* 注:与AOV网不同的是,AOV网是顶点表示活动的网,它值描述活动之间的制约关系,而AOE网是
* 用边表示活动的网,边上的权值表示活动持续的时间。
*/
public class CriticalPath {
/**
* 顶点数组
*/
private List vexList;
/**
* etv:earliest time of vertex 事件的最早发生时间
* ltv:latest time of vertex 事件的最晚发生时间
*/
private int etv[], ltv[];
/**
* 拓扑序列,保存各顶点拓扑排序的顺序
*/
private Stack stack2;
/**
* 创建图1(邻接表)
*/
public void createGraph1() {
//v0
VertexNode v0 = new VertexNode(0, 0, null);
EdgeNode v0e0 = new EdgeNode(3, 3, null);
v0.setFirstEdge(v0e0);
//v1
VertexNode v1 = new VertexNode(0, 1, null);
EdgeNode v1e0 = new EdgeNode(3, 1, null);
EdgeNode v1e1 = new EdgeNode(4, 2, null);
v1.setFirstEdge(v1e0);
v1e0.setNext(v1e1);
//v2
VertexNode v2 = new VertexNode(0, 2, null);
EdgeNode v2e0 = new EdgeNode(4, 3, null);
v2.setFirstEdge(v2e0);
//v3
VertexNode v3 = new VertexNode(2, 3, null);
EdgeNode v3e0 = new EdgeNode(5, 1, null);
v3.setFirstEdge(v3e0);
//v4
VertexNode v4 = new VertexNode(2, 4, null);
EdgeNode v4e0 = new EdgeNode(5, 1, null);
v4.setFirstEdge(v4e0);
//v5
VertexNode v5 = new VertexNode(2, 5, null);
vexList = new ArrayList<>();
vexList.add(v0);
vexList.add(v1);
vexList.add(v2);
vexList.add(v3);
vexList.add(v4);
vexList.add(v5);
}
/**
* 创建图2(邻接表)
*/
public void createGraph2() {
//v0
VertexNode v0 = new VertexNode(0, 0, null);
EdgeNode v0e0 = new EdgeNode(2, 4, null);
EdgeNode v0e1 = new EdgeNode(1, 3, null);
v0.setFirstEdge(v0e0);
v0e0.setNext(v0e1);
//v1
VertexNode v1 = new VertexNode(1, 1, null);
EdgeNode v1e0 = new EdgeNode(4, 6, null);
EdgeNode v1e1 = new EdgeNode(3, 5, null);
v1.setFirstEdge(v1e0);
v1e0.setNext(v1e1);
//v2
VertexNode v2 = new VertexNode(1, 2, null);
EdgeNode v2e0 = new EdgeNode(5, 7, null);
EdgeNode v2e1 = new EdgeNode(3, 8, null);
v2.setFirstEdge(v2e0);
v2e0.setNext(v2e1);
//v3
VertexNode v3 = new VertexNode(2, 3, null);
EdgeNode v3e0 = new EdgeNode(4, 3, null);
v3.setFirstEdge(v3e0);
//v4
VertexNode v4 = new VertexNode(2, 4, null);
EdgeNode v4e0 = new EdgeNode(7, 4, null);
EdgeNode v4e1 = new EdgeNode(6, 9, null);
v4.setFirstEdge(v4e0);
v4e0.setNext(v4e1);
//v5
VertexNode v5 = new VertexNode(1, 5, null);
EdgeNode v5e0 = new EdgeNode(7, 6, null);
v5.setFirstEdge(v5e0);
//v6
VertexNode v6 = new VertexNode(1, 6, null);
EdgeNode v6e0 = new EdgeNode(9, 2, null);
v6.setFirstEdge(v6e0);
//v7
VertexNode v7 = new VertexNode(2, 7, null);
EdgeNode v7e0 = new EdgeNode(8, 5, null);
v7.setFirstEdge(v7e0);
//v8
VertexNode v8 = new VertexNode(1, 8, null);
EdgeNode v8e0 = new EdgeNode(9, 3, null);
v8.setFirstEdge(v8e0);
//v9
VertexNode v9 = new VertexNode(2, 9, null);
vexList = new ArrayList<>();
vexList.add(v0);
vexList.add(v1);
vexList.add(v2);
vexList.add(v3);
vexList.add(v4);
vexList.add(v5);
vexList.add(v6);
vexList.add(v7);
vexList.add(v8);
vexList.add(v9);
}
/**
* 拓扑排序 用于关键路径计算
*
* 新加了一些代码
*/
public boolean topologicalSort() {
//统计输出顶点数
int count = 0;
//建栈存储入度为0的顶点
Stack stack = new Stack<>();
//统计入度数
for (int i = 0;i < vexList.size(); i++) {
vexList.get(i).setIn(0);
}
for (int i = 0;i < vexList.size(); i++) {
EdgeNode edge = vexList.get(i).getFirstEdge();
while (edge != null) {
VertexNode vex = vexList.get(edge.getAdjvex());
vex.setIn(vex.getIn() + 1);
edge = edge.getNext();
}
}
//将入度为0 的顶点入栈
for (int i = 0;i < vexList.size(); i++) {
if (vexList.get(i).getIn() == 0) {
stack.push(i);
}
}
//----新加begin---- 初始化
etv = new int[vexList.size()];
stack2 = new Stack<>();
//----新加end----
System.out.print("拓扑序列:");
while (!stack.isEmpty()) {
//栈顶 顶点出栈
int vexIndex = stack.pop();
System.out.print(vexIndex + " ");
count++;
//----新加 。将弹出的顶点序号压入拓扑序列的栈
stack2.push(vexIndex);
EdgeNode edge = null;
//----循环方式变了一下
for (edge = vexList.get(vexIndex).getFirstEdge(); edge != null; edge = edge.getNext()){
int adjvex = edge.getAdjvex();
VertexNode vex = vexList.get(adjvex);
//将此 顶点的入度减一
vex.setIn(vex.getIn() - 1);
//此顶点的入度为零则入栈,以便于下次循环输出
if (vex.getIn() == 0) {
stack.push(adjvex);
}
//----新加 求各顶点的最早发生时间值。
if (etv[vexIndex] + edge.getWeight() > etv[adjvex]) {
etv[adjvex] = etv[vexIndex] + edge.getWeight();
}
}
}
if (count != vexList.size())
return false;
else
return true;
}
/**
* 关键路径
*/
public void criticalPath() {
//求拓扑序列,计算数组etv和stack2的值
boolean success = topologicalSort();
if (!success) {
System.out.println("\n有回路");
return;
}
//声明活动最早发生时间和最迟发生时间
int ete, lte;
//初始化ltv
ltv = new int[vexList.size()];
for (int i = 0; i : %d\n",
vexList.get(i).getData(), vexList.get(adjvex).getData(), edge.getWeight());
}
}
}
}
public static void main(String[] args) {
CriticalPath criticalPath = new CriticalPath();
criticalPath.createGraph1();
//criticalPath.createGraph2();
criticalPath.criticalPath();
}
}
/**
* 边表结点
*
*/
class EdgeNode {
/**
* 邻接点域,存储该顶点对应的下标
*/
private int adjvex;
/**
* 用于存储权值,对于非网图可以不需要
*/
private int weight;
/**
* 链域,指向下一个邻接点
*/
private EdgeNode next;
public EdgeNode(int adjvex, int weight, EdgeNode next) {
super();
this.adjvex = adjvex;
this.weight = weight;
this.next = next;
}
public int getAdjvex() {
return adjvex;
}
public void setAdjvex(int adjvex) {
this.adjvex = adjvex;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public EdgeNode getNext() {
return next;
}
public void setNext(EdgeNode next) {
this.next = next;
}
}
/**
* 顶点表结点
*
*/
class VertexNode {
/**
* 顶点入度
*/
private int in;
/**
* 顶点域,存储顶点信息(下标)
*/
private int data;
/**
* 边表头指针
*/
private EdgeNode firstEdge;
public VertexNode(int in, int data, EdgeNode firstEdge) {
super();
this.in = in;
this.data = data;
this.firstEdge = firstEdge;
}
public int getIn() {
return in;
}
public void setIn(int in) {
this.in = in;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public EdgeNode getFirstEdge() {
return firstEdge;
}
public void setFirstEdge(EdgeNode firstEdge) {
this.firstEdge = firstEdge;
}
}
结果:
图1:
图2: