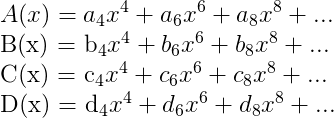uva12298(Super Poker II)-FFT(快速傅里叶变换)
题目链接:Super Poker II
题意:
有一副超级扑克牌,超级扑克牌由四个花色组成,每个花色都有无数张牌,扑克牌的面值p满足条件:p的约数的个数大于2,
即扑克牌的面值为:4,6,8,9,10,12,...(不包括1和素数的自然数)
现在这幅扑克牌丢失了c张,问你从剩余的扑克牌的4个花色中各选出一张牌来,四个花色的面值之和组成一个新的值,
问分别有多少种选法能组成值a, a+1, a+2,...,b。 输出b-a+1行,每行一个数代表选法的个数。
解法:
如图,分别用多项式A(x), B(x), C(x), D(x) 表示扑克牌的四种花色,
当没有牌丢失的时候,系数全为1,当有牌丢失的时候,系数为0,比如,第一种花色的面值为6的牌丢失,则a6 = 0。
那么四个多项式求卷积![]()
则值t的选法个数就是 x^t 的系数 zt,但是这样做复杂度非常高,是o(n^4),所以求卷积要用FFT来优化时间复杂度,
分别对多项式A(x),B(x),C(x),D(x)用FFT进行求值,时间复杂度为o(n*log(n)),将系数表示法转化为点值表示法,
然后直接相乘得到Z(x)的点值表示法,时间复杂度为o(n),然后对Z(x)进行FFT逆变换(插值操作),将点值表示法转化为
系数表示法,这样就可以将求卷积的总的时间复杂度降为o(n*log(n)),然后多项式Z(x)的系数即为答案。
另外,FFT的精度损失比较严重,而这个题需要求四个多项式的卷积,精度损失更加严重,需要用long double
代码:
# pragma comment(linker, "/STACK:1024000000,1024000000")
# include
# include
# include
# include
# include
# include
using namespace std;
typedef long long ll;
const long double PI = acos(-1.0);
const int maxn = 500000 + 5;
bitset is_pri;
struct Complex {
long double x, y;
Complex() : x(0.0), y(0.0) { }
Complex(long double x, long double y) : x(x), y(y) { }
Complex operator - (const Complex &b) const {
return Complex(x - b.x, y - b.y);
}
Complex operator + (const Complex &b) const {
return Complex(x + b.x, y + b.y);
}
Complex operator * (const Complex &b) const {
return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
}
} x[4][maxn];
void change(Complex y[], int len) {
int i, j, k;
for (i = 1, j = len / 2; i < len - 1; i++) {
if (i < j) swap(y[i], y[j]);
k = len / 2;
while (j >= k) {
j -= k; k /= 2;
}
if (j < k) j += k;
}
}
void fft(Complex y[], int len, int on) {
change(y, len);
for (int h = 2; h <= len; h <<= 1) {
Complex wn(cos(-on * 2 * PI / h), sin(-on * 2 * PI / h));
for (int j = 0; j < len; j += h) {
Complex w(1, 0);
for (int k = j; k < j + h / 2; k++) {
Complex u = y[k];
Complex t = w * y[k + h / 2];
y[k] = u + t;
y[k + h / 2] = u - t;
w = w * wn;
}
}
}
if(on == -1)
for (int i = 0; i < len; i++) y[i].x /= len;
}
void init() {
is_pri.set();
is_pri[0] = is_pri[1] = 0;
int t = sqrt(maxn + 0.5);
for (int i = 2; i <= t; ++i)
if (is_pri[i])
for (int j = i * i; j < maxn; j += i)
is_pri[j] = 0;
}
int to(char ch) {
if (ch == 'S') return 0;
else if (ch == 'H') return 1;
else if (ch == 'C') return 2;
else if (ch == 'D') return 3;
}
int main(void)
{
int a, b, c; init();
while (~scanf("%d %d %d", &a, &b, &c) && (a || b || c)) {
int len0 = b + 1, len = 1;
while (len < len0) len <<= 1;
len <<= 2;
for (int i = 0; i < 4; ++i) {
x[i][0] = x[i][1] = Complex(0.0, 0.0);
for (int j = 2; j < len0; ++j) {
if (!is_pri[j]) x[i][j] = Complex(1.0, 0.0);
else x[i][j] = Complex(0.0, 0.0);
}
for (int j = len0; j < len; ++j) x[i][j] = Complex(0.0, 0.0);
}
for (int i = 0; i < c; ++i) {
int val; char ch; scanf("%d%c", &val, &ch);
x[to(ch)][val].x = 0.0;
}
for (int i = 0; i < 4; ++i) fft(x[i], len, 1);
for (int i = 0; i < len; ++i) x[0][i] = x[0][i] * x[1][i] * x[2][i] * x[3][i];
fft(x[0], len, -1);
for (int i = a; i <= b; ++i)
printf("%lld\n", (ll)(x[0][i].x + 0.5));
puts("");
}
return 0;
}