推荐系统-Ctr点击率预估理论基础及项目实战

Ctr点击率预估理论基础及项目实战

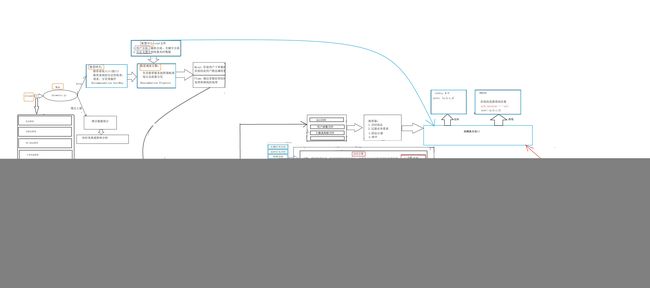
1.机器学习推荐算法模型回顾

• 召回(粗排)
  • 利用业务规则结合机器学习推荐算法得到初始推荐结果，得到部分商品召回集
  • ALS\UserCF\ItemCF\FP-Growth\规则等方式召回
• 排序(精排)
  • 1期：根据不同推荐位通过不同的模型得到推荐结果
  • 2期：将推荐的所有结果通过Ctr或Cvr预估结果进行排序
  • GBDT\LR\GBDT+LR\FM()\FFM()\DeepFM\Wide and deep模型\PNN()\FNN()等​
• 结构图示

扩展 : 推荐系统排序模型

• 框架

​ 从框架的角度看，推荐系统基本可以分为数据层、触发层、融合过滤层和排序层。数据层包括数据生成和数据存储，主要是利用各种数据处理工具对原始日志进行清洗，处理成格式化的数据，落地到不同类型的存储系统中，供下游的算法和模型使用。候选集触发层主要是从用户的历史行为、实时行为、地理位置等角度利用各种触发策略产生推荐的候选集(召回)。候选集融合和过滤层有两个功能，一是对出发层产生的不同候选集进行融合，提高推荐策略的覆盖度和精度；另外还要承担一定的过滤职责，从产品、运营的角度确定一些人工规则，过滤掉不符合条件的item。排序层主要是利用机器学习的模型对触发层筛选出来的候选集进行重排序。

​ 首先将客户上报过来的数据进行数据清洗，检查数据的一致性，处理无效值和缺失值等，去除脏数据，处理成格式化数据存储到不同类型的存储系统中。对于用户行为日志和推荐日志由于随时间积累会越来越大，一般存储在分布式文件系统(HDFS)，即Hive表中，当需要的时候可以下载到本地进行离线分析。对于物品信息一般存储在MySQL中，但是对于业务数据，越来越多的客户导致物品信息表(item_info)越来越大，所以同时也会保存在Hive表和HBase中，Hive可以方便离线分析时操作，但实时程序读取的时候Hive表的实时性较差，所以同时也会写一份放在HBase中供实时程序读取。对于各个程序模块生成的结果，有进程同步关系的程序一般会使用Redis作为缓冲存储，生产者会把信息写到redis中供消费者使用。候选集生成是从用户的历史行为、实时行为、利用各种策略和算法生成推荐的候选集。同时点击反馈会根据用户的实时操作对候选集进行实时的调整，对于部分新用户和历史行为不太丰富的用户，由于候选集太小，需要一些替补策略进行补充。候选集融合规则过滤主要有两个功能，一是对生成的候选集进行融合，提高推荐策略的覆盖度和精度;另外还需根据产品、运营的角度确定一些人为的规则，过滤掉不符合条件的item，重排序主要是利用机器学习的模型对融合后的候选集进行重排序。

​ 同时，对与候选集触发和重排序两层而言，为了效果迭代是需要频繁修改的两层，因此需要支持ABtest。为了支持高效率的迭代，我们对候选集触发和重排序两层进行了解耦，这两层的结果是正交的，因此可以分别进行对比试验，不会相互影响。同时在每一层的内部，我们会根据用户将流量划分为多份，支持多个策略同时在线对比。

​ 排序模型分为非线性模型和线性模型，非线性模型能较好的捕捉特征中的非线性关系，但训练和预测的代价相对线性模型要高一些，这也导致了非线性模型的更新周期相对要长。相较而言，线性模型对特征的处理要求比较高(LR对特征要求较高)，需要凭借领域知识和经验人工对特征做一些先期处理，但因为线性模型简单，在训练和预测时效率较高。因此在更新周期上也可以做的更短，还可以结合业务做一些在线学习的尝试。

2.机器学习重排序-线性模型

• 逻辑斯特回归是一种广义线性模型 , 虽然名字里带着回归 , 但它其实是一种分类算法 , 主要运用在二分类或多分类算法 . 逻辑斯特回归采用极大似然法对模型参数进行估计 .
• 线性模型以LR为例展开
  • 线性回归：y=w0+w1x1+w2x2+w3x3
  • 非线性函数：y=1/{1+e**-x} — sigmod函数 — 以概率输出2分类的结果
• 线性模型：对输入特征需要做专门的处理灌入算法中学习

3.机器学习重排序-非线性模型

• GBDT为例—梯度提升决策树
  • 算法原理：
    • 加法模型
    • 前线分布算法
    • 梯度下降法
  • 是非线性模型，在模型中数据的输入没有要求，比线性模型少了很多的处理特征的环境

4.机器学习重排序-GBDT+LR简介

• GBDT+LR
  • GBDT天然具有的优势是可以发现多种有区分性的特征以及特征组合 .
  • LR利用GBDT的输出结果作为输入 ; LR要输入的是线性独立特征
• GBDT是非线性模型
• LR是线性模型
• LR特征工程比较困难，可以借助GBDT方法得到关键特征
• GBDT通过将样本落入到每一个叶子结点上，取值为1，其余为0，构建稀疏性向量空间，如01001，将新向量作为LR的输入进行点击率预估，以概率的形式输出点击率预估结果

5.排序模型发展

• LR阶段--------特征需要处理
• 为什么LR需要线性独立的特征？
  • LR接受的是线性独立的特征
  • y=w0+w1x1+w2x2 假设x1和x2是相关变量，能够将w1x1+w2x2组合为一个wx
• LR的瓶颈 :
  • 1、特征都需要人工进行转换为线性特征，十分消耗人力，并且质量不能保证
  • 2、特征两两作Interaction (交叉沿镇)的情况下，模型预测复杂度是平方项。在100维稠密特征的情况下，就会有组合出10000维的特征，复杂度高，增加特征困难。
  • 3、三个以上的特征进行Interaction 几乎是不可行的
• GBDT的优点 :
  • 1、对输入特征的分布没有要求
  • 2、根据熵增益自动进行特征转换、特征组合、特征选择和离散化，得到高维的组合特征，省去了人工转换的过程，并且支持了多个特征的Interaction
  • 3、预测复杂度与特征个数无关
• GBDT阶段-------能够做非线性处理
  • 根据信息gini系数对各个特征进行交叉，得到叶子结点是各个特征的交叉的结果，可以利用GBDT算法以稀疏编码的方式对已有的样本进行预测输出，如000101
  • GBDT算法的特点正好可以用来发掘有区分度的特征、特征组合，减少特征工程中人力成本。
• GBDT+LR
  • 利用GBDT的输出作为LR输入，输入LR的特征是独立的特征，进而进行学习

• stacking模型就是上一个模型的结果作为下一个模型的输入

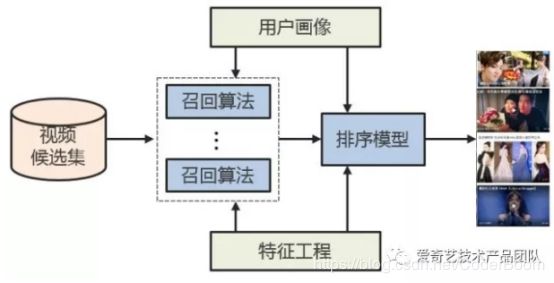
6.爱奇艺推荐排序模型

• 推荐系统的整体结构如图所示，各个模块的作用如下：
  • 1、用户画像：包含用户的人群属性、历史行为、兴趣内容和偏好倾向等多维度的分析，是个性化的基石
  • 2、特征工程：包含了了视频的类别属性，内容分析，人群偏好和统计特征等全方位的描绘和度量，是视频内容和质量分析的基础
  • 3、召回算法：包含了多个通道的召回模型，比如协同过滤，主题模型，内容召回和SNS等通道，能够从视频库中选出多样性的偏好内容
  • 4、排序模型：对多个召回通道的内容进行同一个打分排序，选出最优的少量结果。
• 推荐排序系统架构
  • 在召回阶段，**多个通道的召回的内容是不具有可比性的，**并且因为数据量太大也难以进行更加较精确的偏好和质量评估，因此需要在排序阶段对召回结果进行统一的准确的打分排序。
  • (规则排序)用户对视频的满意度是由很多维度因子来决定的，这些因子在用户满意度中的重要性也各不相同，甚至各个因子之间还有多层依赖关系，人为制定复杂的规则既难以达到好的效果，又不具有可维护性，这就需要借助机器学习的方法，使用机器学习模型来综合多方面的因子进行排序（基于模型排序效果）。
• 机器学习的架构解决了以下两个问题
  • 训练预测的一致性
    • 机器学习模型在训练和预测之间的差异会对模型的准确性产生很大的影响，尤其是模型训练与在线服务时特征不一致，比如用户对推荐结果的反馈会实时影响到用户的偏好特征，在训练的时候用户特征的状态已经发生了变化，模型如果依据这个时候的用户特征就会产生非常大的误差。
    • 我们的解决办法是，将在线服务时的特征保存下来，然后填充到收集的用户行为样本中，这样就保证了训练和预测特征的一致性。 ===> 即增大了数据的复杂度
  • 持续迭代
    • 互联网产品持续迭代上线是常态，在架构设计的时候，数据准备，模型训练和在线服务都必须能够对持续迭代有良好的支持。
    • 我们的解决方案是，数据准备和模型训练各阶段解耦，并且策略配置化，这种架构使模型测试变得非常简单，可以快速并行多个迭代测试。
• 召回
  • 用户画像
  • 特征工程
  • 推荐算法
• 排序
  • 用户行为收集，特征填充，训练样本筛选，模型训练，在线预测排序
  • 机器学习算法

7.极大似然估计

• 求解发生概率的最大值

• 目的：求解发生概率最大值

• 步骤：1.写出似然函数，2.对似然函数求log对数，3.对似然函数求导数，4.得到最优解

• 机器学习三要素：

  • 模型
    • 决策函数：损失函数—平方损失、绝对值损失、指数损失 ----- 最小化损失
    • 条件概率函数：极大似然估计

• 求解极大似然目标函数

  • 步骤：
    • 1.写出似然函数
    • 2.对似然函数求log对数
    • 3.对似然函数求导数
    • 4.得到最优解
  • 图解

极大似然估计的例子图解

8.梯度下降法及牛顿法

• 梯度下降法
  • 底层实现：泰勒的一阶展开
• 代码实现

# 给定初始值 , xOld记录上一步的x值 , xNew下一步迭代的x值
xOld = 0
xNew = 6

# 步长
epa = 0.01

# 可接受误差
precision = 0.00001


# 定义原函数
def f(x):
	return x ** 4 - 3 * x ** 3 + 2


# 定义导函数
def f_prime(x):
	return 4 * x ** 3 - 9 * x ** 2


# 主函数
if __name__ == '__main__':
	# 循环直到函数值之差满足最小误差
	while abs(f(xNew) - f(xOld)) > precision:
		xOld = xNew
		xNew = xOld - epa * f_prime(xOld)
	# 输出极小值点
	print("最小值点为 : ", xNew, "最小值为 : ", f(xNew))
# 最小值点为 :  2.2489469258218673 最小值为 :  -6.542957528732806

• 总结 :
  • （1）方向导数是各个方向上的导数
  • （2）偏导数连续才有梯度存在
  • （3）梯度的方向是方向导数中取到最大值的方向，梯度的值是方向导数的最大值。
• 批量梯度下降法(BGD)
  • 更新规则–所有样本都参与了 theta 的更新和求解，这称之为批量梯度方法，批量梯度下降法可以找到 线性回归的全局最小值（为什么？因为目标函数是凸函数，凸函数有且只有一个全局最小值），但算法本身局限在于可能存在局部最优解，但不是全局最优解。
• 随机梯度下降法(SGD)
  • 特点 : 更快 , 在线 , 可以跳过局部最小值 , 有可能找不到全局最优值 , 有时候会在局部最优值点发生震荡 , 但是一般情况下在一定位置发生震荡 , 认为模型收敛了 . SGD比BGD更能收敛到全局最优值

• 牛顿法 :
  • 底层实现：泰勒二阶展开
• 牛顿法代码 :

# 定义原函数
def f(x):
	return x ** 3.0 - 2.0


# 定义导函数
def df(x):
	return 3.0 * x ** 2.0


# 定义迭代值
def g(x):
	return x - f(x) / df(x)


# 定义初始值
x = 1.0
# 定义误差
r = 1.0

# 循环100次
for i in range(100):
	# 迭代值赋值
	x1 = g(x);
	# 误差赋值
	r = abs(x1 - x)
	# 可接受误差
	if r < 1e-10:
		print("step : % d " % i)
		break
	# 更新下一步起始位置
	x = x1
	# 显示迭代步骤
	print("step : %d , x = %f" % (i, x))
print("remaind error = %f" % r)
print("x = %f" % x)
print("check f(x) = %f , the result is %r" % (f(x), f(x) == 0))
# step : 0 , x = 1.333333
# step : 1 , x = 1.263889
# step : 2 , x = 1.259933
# step : 3 , x = 1.259921
# step : 4 , x = 1.259921
# step :  5 
# remaind error = 0.000000
# x = 1.259921
# check f(x) = 0.000000 , the result is True

• 梯度下降法与牛顿法的比较

9.逻辑斯特回归模型

• 构建似然函数
• 对似然函数加log对数----------------负log损失函数-------交叉熵损失
• 求解导数
• 利用梯度下降法求解得到参数
  • BGD
  • SGD(Mini-Batch SGD)

• 掌握手推梯度下降法

10.逻辑斯特回归模型实践

• 逻辑回归可以解决分类问题
• 参数信息：solver和penlty正则项

#导入数据
from sklearn.datasets import load_iris
iris=load_iris()
#数据的基础属性信息
print(iris.data)
print(iris.target)
#建立模型
X=iris.data
y=iris.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=22)
from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(solver='newton-cg')
lr.fit(X_train,y_train)
#模型检验
print("lr model in trainset score:",lr.score(X_train,y_train))
print("lr model in testset score:",lr.score(X_test,y_test))
# lr model in trainset score: 0.9416666666666667
# lr model in testset score: 0.9666666666666667

11.线性回归和逻辑回归的API

• 通过sklearn的API实现不同的算法

12.GBDT_LR实战与总结

• GBDT+LR实战

• GBDT形成结果通过OneHot编码形成没有线性关系的独热编码

• 再通过LR输出0-1之间的概率值

• sklearn中https://scikit-learn.org/stable/auto_examples/ensemble/plot_feature_transformation.html

• 测试代码

import numpy as np
np.random.seed(10)

import matplotlib.pyplot as plt

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import (RandomTreesEmbedding, RandomForestClassifier,
                              GradientBoostingClassifier)
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve
from sklearn.pipeline import make_pipeline

n_estimator = 10
X, y = make_classification(n_samples=80000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
X_train, X_train_lr, y_train, y_train_lr = train_test_split(
    X_train, y_train, test_size=0.5)


# Supervised transformation based on gradient boosted trees
grd = GradientBoostingClassifier(n_estimators=n_estimator)
grd_enc = OneHotEncoder()
grd_lm = LogisticRegression(solver='lbfgs', max_iter=1000)

grd.fit(X_train, y_train)
grd_enc.fit(grd.apply(X_train)[:, :, 0])
grd_lm.fit(grd_enc.transform(grd.apply(X_train_lr)[:, :, 0]), y_train_lr)

y_pred_grd_lm = grd_lm.predict_proba(grd_enc.transform(grd.apply(X_test)[:, :, 0]))[:, 1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred_grd_lm)

# # The gradient boosted model by itself
# y_pred_grd = grd.predict_proba(X_test)[:, 1]
# fpr_grd, tpr_grd, _ = roc_curve(y_test, y_pred_grd)
plt.plot(fpr_grd_lm,tpr_grd_lm)
plt.show()

**每个样本都经过整体的每棵树的决定，并以每棵树的一片叶子结束。**通过将这些叶的特征值设置为1并将其他特征值设置为0来对样本进行编码。
然后，所得到的transformer学习数据的监督的，稀疏的，高维的分类嵌入。

http://scikit-learn.org/stable/modules/generated/sklearn.metrics.auc.html#sklearn.metrics.auc
http://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_auc_score.html#sklearn.metrics.roc_auc_score
http://scikit-learn.org/stable/auto_examples/ensemble/plot_feature_transformation.html

• 算法背景 : acebook发表了一篇介绍将GBDT+LR模型用于其广告推荐系统的论文

• LR模型有以下特点：

  • 计算复杂度低
  • 易于并行化处理???
  • 易于得到离散化目标值0或1，利用sigmoid函数将传统线性模型的输出值映射到(0,1)区间

• GBDT作为一种常用的树模型，可天然地对原始特征进行特征划分、特征组合和特征选择，并得到高阶特征属性和非线性映射。从而可将GBDT模型抽象为一个特征处理器，通过GBDT分析原始特征获取到更利于LR分析的新特征。这也正是GBDT+LR模型的核心思想——利用GBDT构造的新特征来训练LR模型。

• 算法原理及实现

  • 算法组合——stacking : stacking方法有些类似于农业中的嫁接，通过stacking方法组合的模型亦类似于嫁接植物
  • Facebook论文中的GBDT+LR模型就采用了GBDT算法作为学习层，以LR算法为输出层。

• 算法流程& 代码简单实现

  • 数据预处理 : 对变量取值中的中英文字符、缺失值和正负无穷值进行处理。
  • 数据集划分 : 为了降低过拟合的风险，将训练集中的数据划分为两部分，一部分数据用于训练GBDT模型，另一部分数据通过训练好的GBDT模型得到新特征以训练LR模型。

  From sklearn.model import train_test_split
  X_gbdt,X_lr,y_gbdt,y_lr= train_test_split(X,y,test_size=0.5)
  

  • GBDT特征转化 : 首先，通过sklearn中的GradientBoostingClassifier得到GBDT模型，然后使用GBDT模型的fit方法训练模型，最后使用GBDT模型的apply方法得到新特征。

  from sklearn.ensemble import GradientBoostingClassifier
  gbdt = GradientBoostingClassifier()
  gbdt.fit(X_gbdt,y_gbdt)
  leaves = gbdt.apply(X_lr)[:,:,0]
  

  • 特征独热化 : 使用sklearn.preprocessing中的OneHotEncoder将GBDT所得特征独热化。

  from sklearn.preprocessing import OneHotEncoder
  featutes_trans =OneHotEncoder.fit_transform(leaves)
  

  • LR进行分类 : 用经过离散化处理的新特征训练LR模型并得到预测结果。

  from sklearn.linear_model import LogisticRegression
  lr= LogisticRegression()
  lr.fit(features_trans,y_lr)
  lr.predict(features_trans)
  lr.predict_proba(features_trans)[:,1]
  

• 调参方法简述 :

  ​ 构建了模型框架后，模型中的函数参数调整也是必不可少的。对模型参数的适当调整，往往可以有效提升模型的效果。
  ​ 由于GBDT+LR模型无法整体使用GridSearchCV函数，所以调参时
  ​ 使用sklearn.cross_validation中的StratifiedKFold方法，将数据集进行k折交叉切分，然后以auc值为模型评估指标，对混合模型进行调参。
  ​ 调参时的重点为GradientBoostingClassifier函数，可用如下图所示的调参顺序进行调参。
  ​ 其中，n_estimators和learning_rate应该联合调参。

• 模型效果展示

  ​ 我们分别使用LR模型和GBDT+LR模型对样本数据集进行学习，通过模型所得的auc值和ks值，来评估和比较模型的效果。

• 算法引申
  • 用FFM模型替代LR模型：
  • 直接将GBDT所得特征输入FFM模型；
  • 用XGBoost模型替代GBDT模型；
  • 将stacking模型学习层中的GBDT交叉检验；
  • GBDT和LR模型使用model fusion，而不是stacking

扩展 : 【实战】GBDT+LR算法进行特征扩增

• 简介

  ​ CTR估计也就是广告点击率预估，计算广告训练与平滑思想说明了是用LR算法对于预测的有效性。LR（Logistic Regression）是广义线性模型，与传统线性模型相比，**LR通过Logit变换将函数值映射到0~1区间，映射后的函数就是CTR的预估值。**LR模型十分适合并行化，因此对于大数据的训练十分有效。但是对于线性模型而言，学习能力是有限的，因此需要大量的特征工程预先分析出有效的特征或者是特征组合，从而去间接的增强LR的非线性学习能力。
  ​ 特征组合，是通过特征的一些线性叠加或者非线性叠加得到一个新的特征，可以有效的提高分类效果。常见的特征组合方式有笛卡尔积方式。为了降低人工组合特征的工作量，FaceBook提出了一个自动特征提取的方式GBDT+LR。

  ​ GBDT是梯度提升决策树，首先会构造一个决策树，首先在已有的模型和实际样本输出的残差上再构造一颗决策树，不断地进行迭代。每一次迭代都会产生一个增益较大的分类特征，因此GBDT树有多少个叶子节点，得到的特征空间就有多大，并将该特征作为LR模型的输入。

• 核心问题

  • （1）建树采用ensemble决策树？

    ​ 一棵树的区分性是具有一定的限制的，但是多棵树可以获取多个具有区分度的特征组合，而且GBDT的每一棵树都会学习前面的树的不足。

  • （2）建树算法为什么采用GBDT而不是RF?

    ​ 对于GBDT而言，前面的树，特征分裂主要体现在对多数样本的具有区分度的特征；后面的树，主要体现的是经过前面n棵树，残差依然比较大的少数样本。优先选用在整体上具有区分度的特征，再选用针对少数样本有区分度的特征。

• 代码实现

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier,RandomForestClassifier
import xgboost as xgb
from xgboost.sklearn import XGBClassifier
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import roc_curve,roc_auc_score,confusion_matrix,classification_report
#1.随机生成数据集
np.random.seed(10)
X,y = make_classification(n_samples=1000,n_features=30)

#2.切分数据
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=223,test_size=0.5)
X_train,X_train_lr,y_train,y_train_lr = train_test_split(X_train,y_train,random_state=223,test_size=0.2)

#4.网格搜索



#5.训练模型
#5.1 RandomForest + LogisticRegression
def RF_LR():
    # Rf: 训练模型
    rf = RandomForestClassifier(n_estimators=100, max_depth=4)#n_estimators:树的数目
    rf.fit(X_train, y_train)
    rf_result = rf.apply(X_train)#apply得到叶子节点的索引

    #onehot编码
    ohe = OneHotEncoder()
    ohe.fit(rf_result)
    # 利用RF模型获取以X_train_lr为输入的叶子节点的索引值, 并对其进行one-hot编码
    X_train_leaf_ohe = ohe.transform(rf.apply(X_train_lr))

    #LR: 训练模型
    lr = LogisticRegression(C=0.1, penalty="l2",multi_class='auto')
    lr.fit(X_train_leaf_ohe, y_train_lr)
    #LR: 预测
    y_pred = lr.predict_proba(ohe.transform(rf.apply(X_test)))[:, 1]

    #模型评估
    fpr, tpr, _ = roc_curve(y_test, y_pred)
    auc = roc_auc_score(y_test, y_pred)
    print("RandomForest + LogisticRegression :\n", auc)
    return fpr,tpr

#5.2 XGBoost + LogisticRegression
def XGB_LR():
    # XGBoost: 训练模型
    # nthread: 并行度
    # n_estimators: Number of boosted trees to fit 要拟合树的数目
    # colsample_bytree:Subsample ratio of columns when constructing each tree
    XGB = xgb.XGBClassifier(nthread=4, learning_rate=0.08, n_estimators=100,
                            colsample_bytree=0.5)
    XGB.fit(X_train, y_train)
    XGB_result = XGB.apply(X_train)
    # onehot编码
    ohe = OneHotEncoder()
    ohe.fit(XGB_result)
    X_train__ohe = ohe.transform(XGB.apply(X_train_lr))
    # X_train__ohe = ohe.transform(rf_result)
    # LR: 训练模型
    lr = LogisticRegression(C=0.1, penalty="l2",multi_class='auto')
    lr.fit(X_train__ohe, y_train_lr)
    # LR: 预测
    # y_pred的shape = [n_samples, n_classes]
    y_pred = lr.predict_proba(ohe.transform(XGB.apply(X_test)))[:, 1]
    # 模型评估
    fpr, tpr, _ = roc_curve(y_test, y_pred)
    auc = roc_auc_score(y_test, y_pred)
    print("XGBoost + LogisticRegression :\n", auc)
    return fpr,tpr

#5.3 GradientBoostingClassifier+LR
def GBDT_LR():
    # GBDT: 训练模型
    # n_estimators:迭代次数
    gbdt = GradientBoostingClassifier(n_estimators=100)
    gbdt.fit(X_train, y_train)
    gbdt_result = gbdt.apply(X_train)  # 3维:shape (n_samples, n_estimators, n_classes)
    # onehot编码
    ohe = OneHotEncoder()
    ohe.fit(gbdt_result[:, :, 0])  # gbdt_result[:,:,0]获取GBDT
    # print(ohe.fit(gbdt_result[:,:,0]))
    X_train__ohe = ohe.transform(gbdt.apply(X_train_lr)[:, :, 0])
    # LR: 训练模型
    lr = LogisticRegression(C=0.1, penalty="l2",multi_class='auto')
    lr.fit(X_train__ohe, y_train_lr)
    # LR: 预测
    # y_pred的shape = [n_samples, n_classes]
    y_pred = lr.predict_proba(ohe.transform(gbdt.apply(X_test)[:, :, 0]))[:, 1]
    # 模型评估
    fpr, tpr, _ = roc_curve(y_test, y_pred)
    auc = roc_auc_score(y_test, y_pred)
    print("GBDT + LogisticRegression :\n", auc)
    return fpr,tpr

#5.4 LR
def LR():
    # LR: 训练模型
    lr = LogisticRegression(C=0.1, penalty="l2",multi_class='auto')
    lr.fit(X_train, y_train)
    # LR: 预测
    # y_pred的shape = [n_samples, n_classes]
    y_pred = lr.predict_proba(X_test)[:, 1]
    # 模型评估
    fpr, tpr, _ = roc_curve(y_test, y_pred)
    auc = roc_auc_score(y_test, y_pred)
    print("LogisticRegression :\n", auc)
    return fpr, tpr

#5.4 XGBoost
def XGBoost():
    # XGB: 训练模型
    XGB = xgb.XGBClassifier(nthread=4, learning_rate=0.08, n_estimators=100,
                            colsample_bytree=0.5)
    XGB.fit(X_train, y_train)
    # XGB: 预测
    y_pred = XGB.predict_proba(X_test)[:, 1]
    # 模型评估
    fpr, tpr, _ = roc_curve(y_test, y_pred)
    auc = roc_auc_score(y_test, y_pred)
    print("XGBoost :\n", auc)
    return fpr, tpr


# 主函数

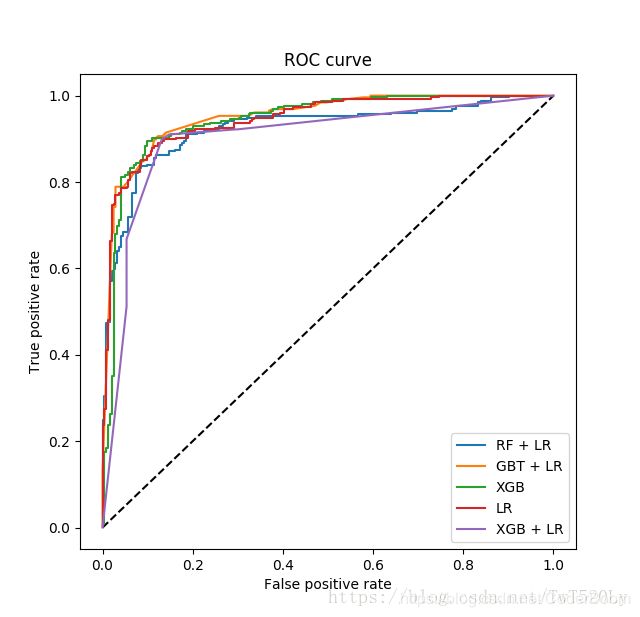
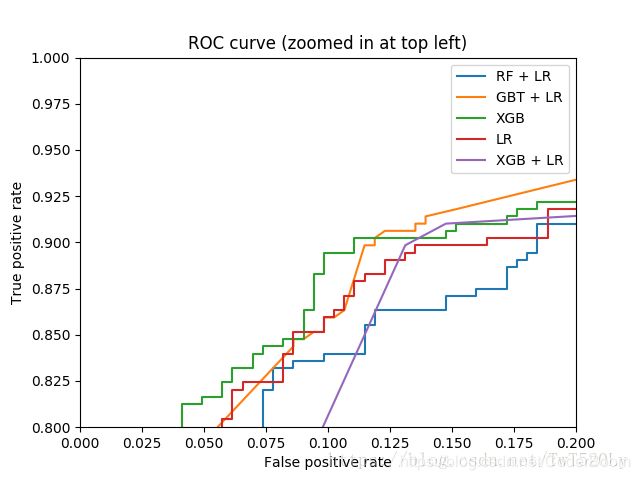
if __name__ == '__main__':
    fpr_rf_lr,tpr_rf_lr = RF_LR()
    fpr_xgb_lr,tpr_xgb_lr = XGB_LR()
    fpr_gbdt_lr, tpr_gbdt_lr = GBDT_LR()
    fpr_lr, tpr_lr = LR()
    fpr_xgb, tpr_xgb = XGBoost()

    # plt.figure(1)
    plt.xlim(0,0.2)
    plt.ylim(0.8,1)
    plt.plot([0, 1], [0, 1], "k--")
    plt.plot(fpr_rf_lr, tpr_rf_lr, label="RF+LR")
    plt.plot(fpr_xgb_lr, tpr_xgb_lr, label="XGB+LR")
    plt.plot(fpr_gbdt_lr, tpr_gbdt_lr, label="GBDT+LR")
    plt.plot(fpr_lr, tpr_lr, label="LR")
    plt.plot(fpr_xgb, tpr_xgb, label="XGBoost")

    plt.xlabel("False positive rate")
    plt.ylabel("True positive rate")
    plt.legend(loc="best")

    plt.show()




# # gbc = GradientBoostingClassifier(loss='exponential',criterion='friedman_mse',presort='auto')
# gbc = GradientBoostingClassifier(loss='deviance',criterion='friedman_mse',presort='auto')
# gbc.fit(X_train,y_train)
#
#
#6.测试数据
# y_pred = gbc.predict(X_test)
#
#7. 模型检测
# print("classification report is: \n", classification_report(y_test,y_pred))

• 参考文献：

https://mp.weixin.qq.com/s?__biz=MzI1ODM5MTI4Nw%3D%3D&chksm=ea09a6badd7e2fac05f9886746bd717bc7e53503906728337b72cd1b95cd2faa4e186e79b9cd&idx=1&mid=2247486242&scene=21&sn=3723bc28c36e0c779bb20aa3f1c92b23
https://blog.csdn.net/lilyth_lilyth/article/details/48032119
https://blog.csdn.net/asdfghjkl1993/article/details/78606268
https://blog.csdn.net/TwT520Ly/article/details/79769705

13.腾讯-GBDT与LR

• GBDT
  • ID树—以不同的id进行分类
  • 非ID树—拿所有样本构建树
• LR
  • 接受GBDT输出结合Onehot编码数据

14.CTR在广告场景应用

• ctr广告场景的引用
  • 搜索类广告
  • 展示类广告
  • 社交类广告
• 计费方式
  • cpm展示既收费----展示到一定次数>100
  • cpc点击即收费-----点击率Ctr*bid — (常见)
  • cpa转化即收费-----需要转换
• 如果ctr不高怎么办？
  • 展示量低？— 提高展示量
  • 展示量高，点击偏低
    • 文案
    • 广告关键词？-----重新购买关键词
    • 推广结果排名较低
• GBDT+LR模型

15.Avazu-CTR-Prediction-LR代码

• 数据源+数据导入
• 数据的基本分析
• 特征工程
• 建立模型
• 模型校验
• 模型预测
• 模型保存

#1.导入数据并进行简单的数据探索
import os
data_path = os.path.join(".", "train_small.csv")
import pandas as pd
ctr_data1 = pd.read_csv(data_path)
#2.数据的简单描述信息
print(ctr_data1.shape)
# print ctr_data.head()
# print ctr_data.describe()
print (ctr_data1.columns)
print ("="*100)
training_Set=ctr_data1.drop(['id','site_id', 'app_id', 'device_id', 'device_ip', 'site_domain',
                  'site_category', 'app_domain', 'app_category', 'device_model'], axis=1)
ctr_data=training_Set.values #numpy--ndarry
#2.对数据进行处理和分析
from sklearn.model_selection import train_test_split
X=ctr_data[:,1:]
print (X.shape)
y=ctr_data[:,0]
print (y.shape)
X_train, X_test, y_train, y_test=train_test_split(X,y,test_size=0.22,random_state=33)
print (X_train.shape)
print (y_train.shape)
# #3.引入机器学习算法
from sklearn.linear_model import LogisticRegression
# lr=LogisticRegression()
#           0       0.83      1.00      0.91     18240
#           1       0.00      0.00      0.00      3760
#
# avg / total       0.69      0.83      0.75     22000
lr=LogisticRegression(C=0.1, penalty= 'l1')
#              precision    recall  f1-score   support
#
#           0       0.83      1.00      0.91     18240
#           1       0.40      0.00      0.00      3760
#
# avg / total       0.76      0.83      0.75     22000
lr.fit(X_train,y_train)
# #4.模型预测
y_pred=lr.predict(X_test)
print (y_pred)
# # #5.模型校验
print( lr.score(X_train,y_train))
print (lr.score(X_test,y_test))
from sklearn.metrics import confusion_matrix
print( confusion_matrix(y_test,y_pred))
from sklearn.metrics import classification_report
print( classification_report(y_test,y_pred))
# #6.保存模型
from sklearn.externals import joblib
joblib.dump(lr,filename="Ctr_Predict.pkl")
# #8.按照要求写入对应的csv文件
import numpy as np
import pandas as pd
ctr_data2=pd.read_csv("test.csv")
ctr_data3=ctr_data2.drop(['click','site_id', 'app_id', 'device_id', 'device_ip', 'site_domain',
                  'site_category', 'app_domain', 'app_category', 'device_model'], axis=1)
print( ctr_data3)
ids=ctr_data3.values[0:,0]
y_pred_test=lr.predict(ctr_data3.values[0:,1:])
# # # print ids
submit=np.concatenate((ids.reshape(len(ids),1),y_pred_test.reshape(len(y_pred_test),1)),axis=1)
df=pd.DataFrame(submit)
df.to_csv("submit.csv", header=['id', 'click'], index=False)

17.Ctr广告点击率预估代码实战

18.Ctr技术发展应用

• 百度蜂巢
• 阿里妈妈
• 京东
  • 规则-------LR--------GBDT提取关键特征------GBDT+LR(分类概率)
  • FM—FFM—DeepFM—WideAndDeep
• FM—能够提取二阶特征----通过隐向量latent vector做内积提取
• FFM—在FM基础上增加了Field(域)概念
• FNN—Filed Neural network–只能学习到高阶特征
• PNN—在神经网络中增加了product-layer
• Wide and Deep===线性回归或LR+DEEP–需要借助人工特征工程
• DeepFM—FM提取一阶和二阶特征—Deep提取高阶特征—Sigmod函数给出预测值

19.总结

• 机器学习基础概念
• 语言基础—Python语言—Scala—Julia—R语言
• (项目1)用户画像—挖掘类标签
• (项目2)推荐系统—基于sparkmllib模型和surprise库模型–tensorflow—召回
• (项目3)推荐结果排序----模型排序
• (项目4)Ctr广告点击率预估\Cvr广告的转化率预估

扩展 2:

区别 :

• 监督学习和非监督学习主要却别在于 : 监督学习有类别标签 , 非监督学习没有类别标签
• 分类和回归的主要区别在于 : 分类的预测值不是连续值 , 而回归的预测值是连续值
• 分类和聚类的主要区别在于 : 分类有类别标签 , 聚类没有
• 生成模型和判别模型的主要区别 : 生成模型主要利用联合概率分布 , 而判别模型主要利用条件概率分布
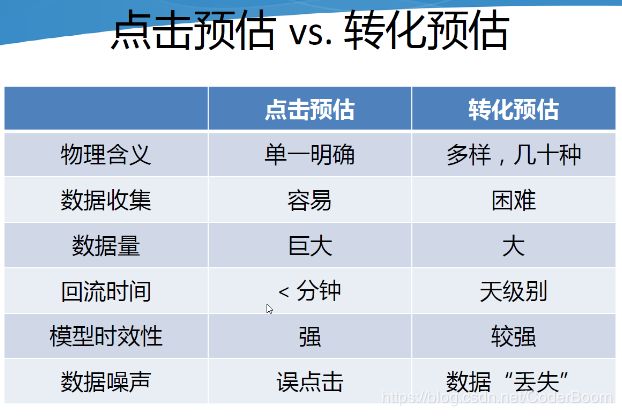
• 点击预估&转化预估

扩展3 :

• CTR预估数据特点：

  • 1.输入中包含类别型和连续型数据。类别型数据需要one-hot,连续型数据可以先离散化再one-hot，也可以直接保留原值
  • 2.维度非常高
  • 3.数据非常稀疏
  • 4.特征按照Field分组
    CTR预估重点在于学习组合特征。

  LR，FTRL。线性模型有个致命的缺点：无法提取高阶的组合特征(线性y=w0+w1+w2等)。
  LR最大的缺点就是无法组合特征，依赖于人工的特征组合，这也直接使得它表达能力受限，基本上只能处理线性可分或近似线性可分的问题。

• FM模型

  FM通过隐向量latent vector做内积来表示组合特征，从理论上解决了低阶和高阶组合特征提取的问题。但是实际应用中受限于计算复杂度，一般也就只考虑到2阶交叉特征。

  后面有进行了改进 , 提出了FFM , 增加了Field的概念

• CNN模型的缺点是：偏向于学习相邻特征的组合特征。 RNN模型的缺点是：比较适用于有序列(时序)关系的数据。

• FNN : 先使用预先训练好的FM，得到隐向量，然后作为DNN的输入来训练模型。缺点在于：受限于FM预训练的效果。

• 随后提出了PNN，PNN为了捕获高阶组合特征，在embedding layer和first hidden layer之间增加了一个product layer。根据product layer使用内积、外积、混合分别衍生出IPNN, OPNN, PNN三种类型。

• 无论是FNN还是PNN , 都避免不了 : 对于低阶的组合特征，学习到的比较少。而前面我们说过，低阶特征对于CTR也是非常重要的。

• 为了同时学习低阶和高阶组合特征，提出了Wide&Deep模型。它混合了一个线性模型（Wide part）和Deep模型(Deep part)。这两部分模型需要不同的输入，而Wide part部分的输入，依旧依赖人工特征工程。

• 这些模型普遍都存在两个问题：

  • 1.偏向于提取低阶或者高阶的组合特征。不能同时提取这两种类型的特征。
  • 2.需要专业的领域知识来做特征工程。

• DeepFM在Wide&Deep的基础上进行改进，成功解决了这两个问题，并做了一些改进，其优势/优点如下：

  • 1.不需要预训练FM得到隐向量
  • 2.不需要人工特征工程
  • 3.能同时学习低阶和高阶的组合特征
  • 4.FM模块和Deep模块共享Feature Embedding部分，可以更快的训练，以及更精确的训练学习

• FNN使用预训练的FM来初始化DNN，然后只有Deep部分，不能学习低阶组合特征。

• FNN缺点 :

  • Embedding的参数受FM的影响，不一定准确
  • 预训练阶段增加了计算复杂度，训练效率低
  • FNN只能学习到高阶的组合特征。模型中没有对低阶特征建模。

• PNN：为了捕获高阶特征。PNN在第一个隐藏层和embedding层之间，增加了一个product layer。

• PNN缺点：

  • 内积外积计算复杂度高。采用近似计算的方法外积没有内积稳定。
  • product layer的输出需要与第一个隐藏层全连接，导致计算复杂度居高不下
  • 和FNN一样，只能学习到高阶的特征组合。没有对于1阶和2阶特征进行建模。

• Wide & Deep设计的初衷是想同时学习低阶和高阶组合特征，但是wide部分需要领域知识进行特征工程。

• Wide&Deep缺点 : 需要特征工程提取低阶组合特征

• DeepFM优点 :

  • 没有用FM去预训练隐向量V，并用V去初始化神经网络。（相比之下FNN就需要预训练FM来初始化DNN）
  • FM模块不是独立的，是跟整个模型一起训练学习得到的。（相比之下Wide&Deep中的Wide和Deep部分是没有共享的）
  • 不需要特征工程。（相比之下Wide&Deep中的Wide部分需要特征工程）
  • 训练效率高。（相比PNN没有那么多参数）

• 上述东西太多太杂 , 记住最核心的 :

  • 没有预训练（no pre-training）
  • 共享Feature Embedding，没有特征工程（no feature engineering）
  • 同时学习低阶和高阶组合特征（capture both low-high-order interaction features）

• 超参数建议

超参数	建议	备注
激活函数	1.IPNN使用tanh ; 2,其余使用ReLU
学习方法	Adam
Dropout	0.6~0.9
隐藏层数量	3~5 , 根据实际数据大小调整
网络形状	constant , 一共有四种 : 固定、增长、下降、菱形	PS:constant效果最好 , 就是隐藏层每一层的神经元的数量相同