Python金融系列第三篇：随机变量和分布

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

第一篇：计算股票回报率，均值和方差

第二篇：简单线性回归

第三篇：随机变量和分布

第四篇：多元线性回归和残差分析

第五篇：现代投资组合理论

第六篇：市场风险

第七篇：Fama-French 多因子模型

---

介绍

在上一章中，我们学习了均值和方差的定义，这是一种点估计方法。点估计意味着使用样本数据来计算单个值，该值用作未来整体未知样本的最佳估计。然而，这是远远不够的，因为点估计可能会是骗人的。我们需要使用更严格的方法来测试我们的想法。这就是我们需要考虑分布和假设检验的原因。随机变量分布几乎是所有定量金融的基础：线性回归，CAPM，Black-Scholes等等都是用到了随机变量分布。

随机变量

首先让我们从随机变量的概念开始。随机变量的数据你可以看做是在画一个数据分布，但是绘制的数据是你 不知道的。举个例子，你去掷骰子，你知道你能获得的骰子每个面的概率都是 1/6，但是你不知道具体的下一个是什么东西。如果我们掷骰子 N 次并且记录每个面的数量，那么这些数字的集合称为离散随机变量。离散变量可以采用有限数量的值。对于我们的例子，我们只能从 {1,2,3,4,5,6} 中取数字。另一种变量是连续随机变量。连续变量可以采用给定范围内的任何值。你可以将回报率视为连续变量，理论上它可以取任何值 (−∞,+∞) 。

分布

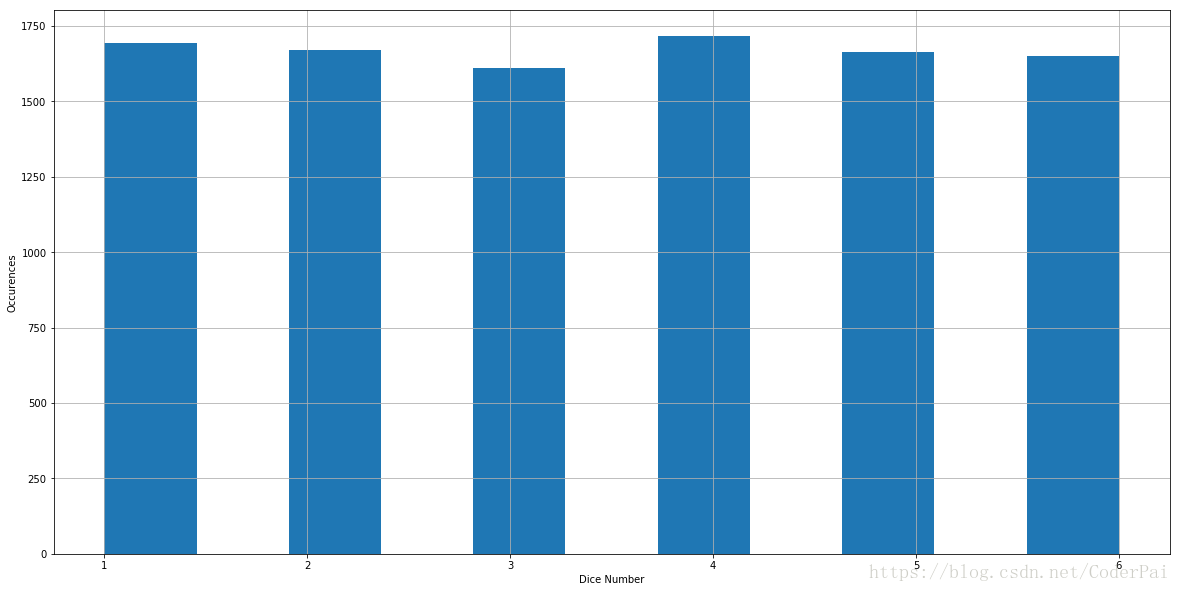
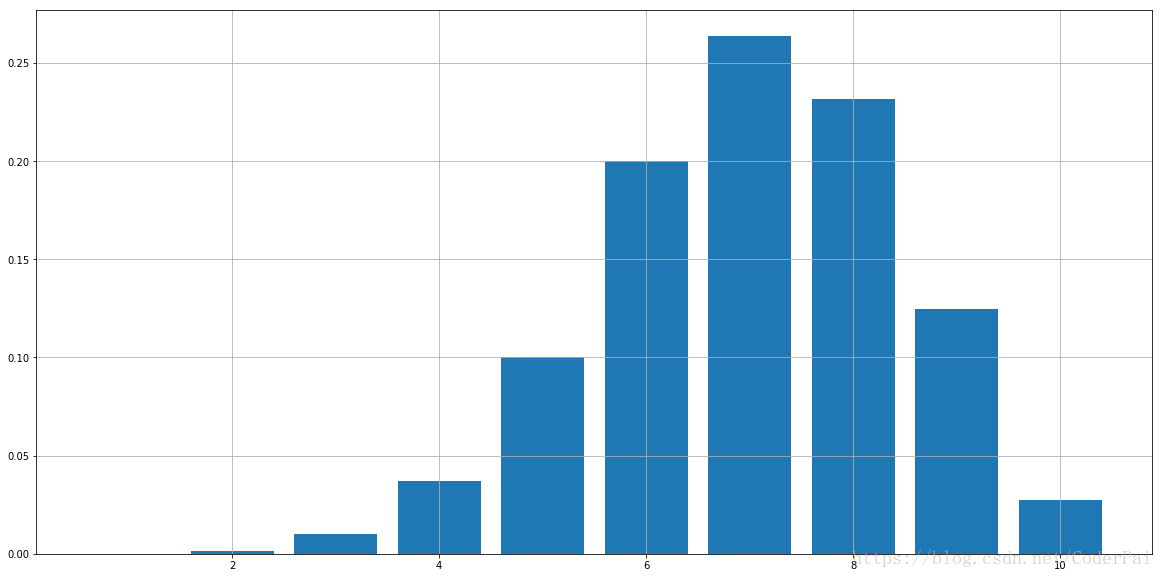
每个随机变量遵循概率分布，该概率分布是可以被认为提供实验中不同可能结果的发生概率的函数。在我们的骰子例子中，每个数字的概率分布都是 1/6 。我们通常使用 P(X) 来表示概率分布函数，其中 X 是结果值。在我们的例子中，P(1) = P(2) = P(3) = 1/6。但是，我们不能将其用于连续分布，因为从连续变量中抽取特定数字的概率为0，因为我们所拥有的候选集合是无限大的。相反，我们使用概率密度函数（PDF）来描述特定范围内的概率。对于每个概率分布函数，我们有一个累积分布函数（CDF）。它的定义是 P(X

均匀分布

均匀分布时最简单的概率分布类型。离散均匀分布具有分配给所有结果的相等权重。掷骰子和掷硬币都是经典的均匀分布问题。在这里我们利用 Python 模拟掷骰子 10000 次。

import random
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#define a function to simulate rolling a dice
def dice():
    number=  [1,2,3,4,5,6]
    return random.choice(number)

series = np.array([dice() for x in range(10000)])
print(series)

我们在这里创建一系列的随机变量。我们可以在 x 轴上绘制值并将它们的出现次数放到 y 轴上面，结果如下：

plt.figure(figsize = (20,10))
plt.hist(series,bins = 11,align = 'mid')
plt.xlabel('Dice Number')
plt.ylabel('Occurences')
plt.grid()
plt.show()

假设我们想要知道观察值小于 3 的概率，换句话说，我们想要寻找 P(X<=3) 的值。

print(len([x for x in series if x <= 3])/float(len(series)))
# [out]: 0.497
print(np.mean(series))
# [out]: 3.4941

P(X<=3) 非常接近 0.5。这并不奇怪，因为我们掷骰子 1000 次，观察值小于或者等于 3 的概率应该非常接近真实概率，即 0.5。对于给定的均匀分布，可以直接计算它的平均值：它是分布的中心，因为每个结构都是相同的权重。对于我们的投资例子，我们可以将其视为：

$\mu =(1+2+3+4+5+6)/6=3.5$

或者：

$E(x)=1\ast \frac{1}{6}+2\ast \frac{1}{6}+3\ast \frac{1}{6}+4\ast \frac{1}{6}+5\ast \frac{1}{6}+6\ast \frac{1}{6}=3.5$

更一般的，如果我们假设均匀分布中的最小值是 a，并且最大值是 b，则平均值可以通过以下的公式给出：

$\bar{\mu }=\frac{a+b}{2}$

通常我们使用 $\bar{\mu }$ 来表示总体的均值。在这里，我们创建一个包含 1000 个观测值的样本，我们在上面计算的平均值是样本均值。除非观察样本数量接近无限大，否则样本均值通常不等于理论总体均值。方差由下列式子给出：

${\sigma }^2=\frac{(b-a{)}^2}{12}$

推导公式超出了我们本文的范围。实现给定的标准分布是非常有用的，我们可以将其均值和方差进行公式化。

二项分布

二项分布是 n 次独立实验序列中成功次数的离散概率分布。让我们假设市场有 50% 的概率上升，50% 的概率下降，我们在接下来的 10 天内观察到它，它上升的天数分布时多少？这是一个二项分布示例。一般来说，如果我们进行 n 次试验，并且每个结果是独立的，也就是具有相同的成功概率 p，则获得 k 次成功的概率函数为：

$P(X=K)=C_n^k{p}^k(1-p{)}^{n-k}$

其中：

$C_n^k=\frac{n!}{(n-k)!k!}$

在这种情况下，我们说变量 X 是遵循二项分布 X~B(n, p) ，让我们来模拟二项试验，成功率 p = 0.7，实验次数是 n = 10。

def trial():
    number = [1,2,3,4,5,6,7,8,9,10]
    a = random.choice(number)
    if a<= 7:
        return 1
    else:
        return 0

我们每次执行 trial() 时，我们都进行了一次实验。如果成功，它将返回 1，否则它将返回 0.现在我们将进行 10 次实验：

res = [trial() for x in range(10)]
print(sum(res))
# [out]: 8

现在我们做了 10 次实验，成功的数量是 sum(res) 。然而，它只是意味着在这 10 个实验中我们成功总和 res 次。如果我们想要看到二项分布，那么我们需要实验 N 次。当 n 足够大时，我们的频率将接近理论概率。在这里，我们模拟 10000 次：

def binomial(number):
    l = []
    for i in range(10000):
        res = [trial() for x in range(10)]
        l.append(sum(res))
    return len([x for x in l if x == number])/float(len(l))
print(binomial(8))
#[out]: 0.2328

上面打印的数字是我们实验 10 次后成功 8 次的模拟概率。对于每个可能的结果，我们模拟概率为：

prob = []
for i in range(1,11):
    prob.append(binomial(i))
prob_s = pd.Series(prob,index = range(1,11))
print(prob_s)
'''
[out]: 1     0.0002
       2     0.0013
       3     0.0087
       4     0.0373
       5     0.1041
       6     0.2000
       7     0.2674
       8     0.2342
       9     0.1153
       10    0.0283
'''

这里我们得到了二项分布的模拟结果。现在我们将检查模拟频率是否接近理论概率。我们以 X = 7 和 X = 8 为例：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)
    
    
print((float(factorial(10))/(factorial(7)*factorial(10-7)))*(0.7**7)*(0.3**3))
#[out]: 0.266827932
print((float(factorial(10))/(factorial(8)*factorial(10-8)))*(0.7**8)*(0.3**2))
#[out]: 0.2334744405

我们可以看到，模拟结果非常接近于真实概率。我们可以将结果绘制如下：

plt.figure(figsize = (20,10))
plt.bar(range(1,11),prob)
plt.grid()
plt.show()

二项分布的另一个好处是它的均值和方差很简单计算：

$\bar{\mu }=np$

${\sigma }^2=np(1-p)$

我们不会推理具体的数学公式，但是记住这些计算公式还是非常有必要的。

正态分布

在查看正太分布之前，让我们先来看看连续分布。正如我们上面提到的，我们使用概率密度函数（PDF）来模拟我们的值取特定范围的概率。我们将其定义为：

$P(a<X<b)={\int }_a^b{f}_x(x)dx$

现在我们可以谈谈正态分布了。正太分布时自然界中最常用的分布，当然也包括金融研究。正太分布的 PDF 如下：

$f(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$

其中，$\mu$ 是正太分布的平均值，$\sigma$ 是标准偏差。

通常，如果一个随机变量 X 遵循正太分布，我们用 X ~ N($\mu$, ${\sigma }^2$) 表示。具体来说，如果正太分布具有均值为 0，标准差为 1，我们将其称为标准正太分布。现在让我们使用 Python 包来模拟标准的正太分布，看看它是如何的：

import scipy.stats as stats
import numpy as np 

x = np.arange(-5,5,0.1)
y=stats.norm.pdf(x, 0,1)
plt.plot(x,y)
plt.show()

财务数据高度混乱，被认为有很多噪音。大多数时候我们认为这些噪音遵循正太分布。人们普遍认为，资产在短时间内的回报也是遵循正太分布。让我们用 SPY 的每日对数收益率来实验一下：

from pandas_datareader import data as pdr
import fix_yahoo_finance as yf

spy_table = pdr.get_data_yahoo("SPY")
spy = spy_table.loc['2009':'2017',['Open','Close']]
spy['log_return'] = np.log(spy.Close).diff()
spy = spy.dropna()

我们计算了从 2009 年到现在的 SPY 的对数日收益率。让我们首先看一下时间序列返回数据的样子：

plt.figure(figsize = (20,10))
spy.log_return.plot()
plt.show()

这是一张经典的每日回归表。现在让我们绘画一下回报的密度图表：

plt.figure(figsize = (20,10))
spy.log_return.plot.density()
plt.show()

如果我们仔细观察 x 轴和 y 轴，我们可以看到资产的回报不是标准的正太分布。标准正太分布图的峰值约为 0.4，而此图表的峰值则超过 0.6。这是因为回报的标准偏差 $\sigma$ 明显不是 1。我们可以通过模拟证明具有不同均值和方差的正太分布：

de_2 = pd.Series(np.random.normal(0,2,10000),name = 'μ = 0, σ = 2')
de_3 = pd.Series(np.random.normal(0,3,10000),name = 'μ = 0, σ = 3')
de_0 = pd.Series(np.random.normal(0,0.5,10000), name ='μ = 0, σ = 0.5')
mu_1 = pd.Series(np.random.normal(-2,1,10000),name ='μ = -2, σ = 1')
df = pd.concat([de_2,de_3,de_0,mu_1],axis = 1)
plt.figure(figsize=(20,10))
df.plot.density()
plt.show()