Python金融系列第四篇：置信区间和假设检验

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

第一篇：计算股票回报率，均值和方差

第二篇：简单线性回归

第三篇：随机变量和分布

第四篇：置信区间和假设检验

第五篇：多元线性回归和残差分析

第六篇：现代投资组合理论

第七篇：市场风险

第八篇：Fama-French 多因子模型

---

介绍

在上一章中，我们讨论了随机变量和随机分布。现在我们将使用我们学到的分布来检验我们的假设，并对财务数据进行建模。在指定交易策略时，进行一些研究是必不可少的工作。但是，你将无法使用所有数据测试你的想法，因为它是无限的。你只能使用样本进行试验。这就是为什么我们需要了解总样本和样本之间的差异，然后使用置信区间来检验我们的假设。

正如我们之前提到的，均值和标准差都是点估计，它们可能是骗人的，因为样本均值与总样本均值不同。将来每天都会产生新的财务数据，因此即使我们可以使用所有可用的数据，但它仍然只是一个样本数据。这就是为什么我们需要使用置信区间来尝试确定我们的样本平均估计的准确度。

置信区间

样本误差

让我们使用从 2010 年 8 月到现在的标准普尔 500 指数的每日回报。如果我们采用最近的 10 个每日回报来计算平均值，它是否与人口平均值相同？如何将样本量增加到 1000？

from pandas_datareader import data as pdr
import fix_yahoo_finance as yf

spy_table = pdr.get_data_yahoo("SPY")
spy_total = spy_table[['Open','Close']]
#calculate log returns
spy_log_return = np.log(spy_total.Close).diff().dropna()
print('Population mean:', np.mean(spy_log_return))
#[out]: Population mean: 0.0004301219214913361
print('Population standard deviation:',np.std(spy_log_return))
#[out]: Population standard deviation: 0.009226632108137144

现在让我们查看最近 10 天的样本和最近 1000 天的样本：

print('10 days sample returns:', np.mean(spy_log_return.tail(10)))
#[out]: 10 days sample returns: -0.0014384211472198594
print('10 days sample standard deviation:', np.std(spy_log_return.tail(10)))
#[out]: 10 days sample standard deviation: 0.003372809234788933
print('1000 days sample returns:', np.mean(spy_log_return.tail(1000)))
#[out]: 1000 days sample returns: 0.0004351380532074112
print('1000 days sample standard deviation:', np.std(spy_log_return.tail(1000)))
#[out]: 1000 days sample standard deviation: 0.00802234416274219

正如我们所料，这两个样本具有不同的均值和方差。

置信区间

为了估计样本平均值的范围，我们定义平均值的标准误差如下：

$SE=\frac{\sigma }{\sqrt{n}}$

其中，$\sigma$ 是样本的标准差，n 是样本的总数。

通常，如果我们想要估计样本区间，一般我们都是使用 95% 为分界线，也就是说我们希望有 95% 的样本可以落在样本区间内，具体如下：

$(\mu -1.96\ast SE,\mu +1.96\ast SE)$

其中，$\mu$ 是样本均值，SE 是标准误差。

此区间称为置信区间。我们通常使用 1.96 来计算 95% 置信区间，因为我们假设样本均值遵循正太分布。我们稍后会详细介绍。让我们尝试使用上面的例子计算置信区间：

#apply the formula above to calculate confidence interval
bottom_1 = np.mean(spy_log_return.tail(10))-1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))
upper_1 = np.mean(spy_log_return.tail(10))+1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))
bottom_2 = np.mean(spy_log_return.tail(1000))-1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))
upper_2 = np.mean(spy_log_return.tail(1000))+1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))
#print the outcomes

print('10 days 95% confidence inverval:', (bottom_1,upper_1))
#[out]: 10 days 95% confidence inverval: (-0.0035289099690756585, 0.0006520676746359399)
print('1000 days 95% confidence inverval:', (bottom_2,upper_2))
#[out]: 1000 days 95% confidence inverval: (-6.209198946181664e-05, 0.000932368095876639)

正如我们所看到的，如果我们将样本大小从 10 增加到 1000，95% 的置信区间将变得更窄。想象一下，如果 N 变为正无穷大，那么我们有 ${\lim }_{n\to \infty }\frac{\sigma }{\sqrt{n}}=0$ 。置信区间将成为一个定值，也就是样本均值。

正太分布的置信区间

正太分布是非常常见的一个分布，我们应该能够记住它的一些关键词。具体而言，我们通常使用 90%，95% 和 99% 作为置信区间的置信水平。这三个置信水平的临界值分别为 1.64，1.96 和 2.32。换一种说法，比如 90% 的置信区间上下界限为：

$upperabnd=\mu +1.64\ast SE$

$lowerband=\mu -1.64\ast SE$

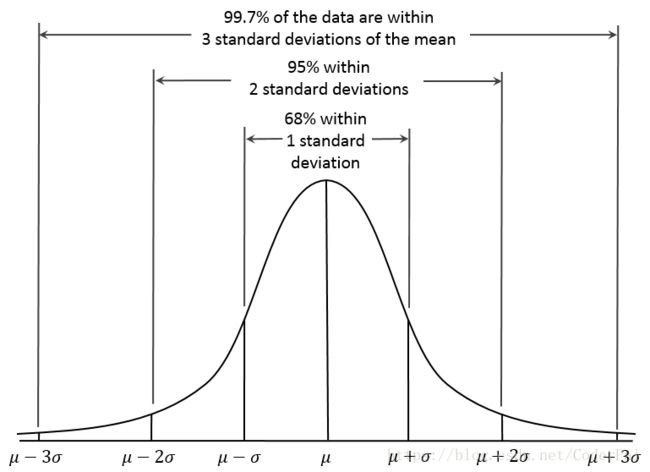
其他置信区间也是如此。记住与正太分布相关的著名的 “Three sigma rule” 或者称为 “68-95-99.7” 。数学上的具体表示为：

$P(\mu -\sigma \le X\le \mu +\sigma )\approx 0.6827$

$P(\mu -2\sigma \le X\le \mu +2\sigma )\approx 0.9545$

$P(\mu -3\sigma \le X\le \mu +3\sigma )\approx 0.9973$

我们也可以用图表来进行表示：

中心极限理论

正如我们所提到的，如果我们使用样本来估计置信区间，那么 95% 置信区间为：

$(\mu -1.96\ast SE,\mu +1.96\ast SE)$

现在你可能对数字 1.96 有了一定的了解。这是正太分布 95% 的临界值。这是否意味着我们假设样本均值遵循正太分布？答案是肯定的。这个假设得到中心极限定理的支持。该定理告诉我们，如果来自具有有限方差水平的裙子的足够大的样本大小，那么来自相同群体的所有样本的平均值将近似等于群体的平均值，并且样本的平均值将近似正太分布。这是群体平均置信区间估计的基础。

假设检验

现在我们可以谈论假设检验。假设检验基本上是根据样本检验你的推理。让我们使用我们的数据集，标普 500 每日回报。假设我们不知道这个数据的平均值。我们先假设一下这个数据的平均值是 0。我的猜测是否正确呢？我需要用我的样本来测试这个假设。让我们从观察我们的样本开始：

mean_1000 = np.mean(spy_log_return.tail(1000))
std_1000 = np.std(spy_log_return.tail(1000))
mean_10 = np.mean(spy_log_return.tail(10))
std_10 = np.std(spy_log_return.tail(10))
s = pd.Series([mean_10,std_10,mean_1000,std_1000],index = ['mean_10', 'std_10','mean_1000','std_1000'])
print(s)

'''
[out]:
mean_10     -0.001438
std_10       0.003373
mean_1000    0.000435
std_1000     0.008022
dtype: float64
'''

我们现在知道如何计算置信区间了。如果我是对的，即总体样本的均值是 0，则样本的 90% 置信区间应该为：

bottom = 0 - 1.64*std_1000/np.sqrt(1000)
upper = 0 + 1.64*std_1000/np.sqrt(1000)
print((bottom, upper))
#[out]: (-0.000416049627539558, 0.000416049627539558)

我们的样本均值超出了 90% 的置信区间。这意味着在 90% 的置信水平上，我们可以声称我们的样本均值不是 0。换句话说，我们拒绝了从 2010 年 8 月起标普 500 指数的每日回报为 0 的假设。那么我们可以认为是拥有 95% 的置信水平吗？

bottom = 0 - 1.96*std_1000/np.sqrt(1000)
upper = 0 + 1.96*std_1000/np.sqrt(1000)
print((bottom, upper))
#[out]: (-0.0004972300426692278, 0.0004972300426692278)

这次样本均值在置信区间内。因此，我不能拒绝我们的假设。换句话说，我们不能以 95% 的置信水平声称平均回报是正的，即使我们能够以 90% 的置信度声称它。我们实际上已经完成了上面的假设检验！一般来说，我们有零假设 $ H_{0}$ 和替代假设。它们通常采用以下形式：

$H_0:\bar{\mu }=0$

$H_0:\bar{\mu }̸=0$

如果测试值超出置信区间，我们拒绝零假设，或者接受替代假设；如果测试值在置信区间内，我们不能拒绝零假设。虽然我们上面使用的假设检验方法非常简单，但是实施起来并不那么方便。相反，我们会颠倒过程来计算临界值或者 Z 分数。Z 分数定义为：

$Z=\frac{X-\mu }{\frac{\sigma }{\sqrt{n}}}$

让我们从样本中计算出 Z 分数：

print(np.sqrt(1000)*(mean_1000 - 0)/std_1000)
#[out]: 1.7152434710263085

我们知道 90% 置信水平的临界值是 1.64，而 95% 置信水平的临界值是 1.96。Z 分数越高，测试值越远离假设值（在该示例中为 0）。因此，在 90% 的置信水平下，我们距离零很远，所以我们拒绝零假设。然而，在 95% 的置信水平下，我们离零点不远，所以我们不能拒绝零假设。这样做的一个原因是我们可以知道我们的置信区间有多宽。在我们的实例中，Z 分数为 1.9488。我们可以知道宽度是指正太分布表的置信区间。当然我们可以用 Python 做到这一点：

import scipy.stats as st
print((1 - st.norm.cdf(1.9488)))
#[out]: 0.02565965688799665

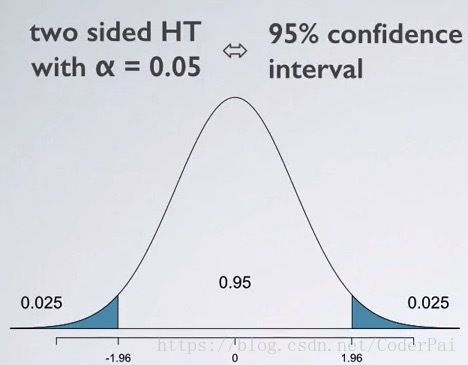
值得注意的是，st.norm.cdf 将返回从分布中获取的值小于我们测试值的概率。换句话说，1 - st.norm.cdf (1.9488) 将返回该值大于我们测试值的概率，在此示例中为 0.025659。该计算出的数字称为 p 值。如果我们的置信水平为 95%，那么左侧为 2.5%，右侧为 2.5%。这称为双尾测试。如果我们的零假设是 $\mu =0$ ，我们正在进行双尾检验，因为测试的样本均值可以是足够的正或者负足以拒绝原假设。我们可以从图表中看到它：

如果我们使用 95% 置信区间，我们需要一个小于 0.025 的p值来拒绝零假设。但是，现在我们的 p 值是 0.025659，大于 0.025，因此我们不能拒绝原假设。它显然小于 0.05，所以我们仍然可以在 90% 置信水平下拒绝零假设。现在让我们用一个答应给你本再次检验总体均值等于 0 的假设，该样本有 1200 个观测值：

mean_1200 = np.mean(spy_log_return.tail(1200))
std_1200 = np.std(spy_log_return.tail(1200))
z_score = np.sqrt(1200)*(mean_1200 - 0)/std_1200
print('z-score = ',z_score)
#[out]: z-score =  2.19793023185
p_value = (1 - st.norm.cdf(z_score))
print('p_value = ',p_value)
#[out]: p_value =  0.0139770390655

使用更大的样本，现在我们可以用更高的置信区间拒绝零假设！我们的 p 值是 0.0105，这是一个双尾测试，所以我们的区间置信度是 1-(0.0105*2) = 0.979。我们可以说最多具有 97.9% 的置信区间，我们可以声称总体均值不为零。我们已经知道人口平均值不是 0，随着我们的样本量增加，我们假设的准确率会上升。