矩阵乘法 GEMM汇编教程(附源码链接)
转载请注明原文链接!!!
项目github源码链接:https://github.com/lyuchuny3/Tengine_gemm_tutorial
GEMM简介
什么是GEMM? 它的英文全称是 GEneral Matrix to Matrix Multiplication (通用矩阵的矩阵乘法). GEMM在神经网络的计算中占据很重要的位置。这篇文章Why gemm is at the heart of deep learning 介绍了为什么GEMM在深度学习计算中占据重要位置,以及卷积计算中是如何使用GEMM的。
教程大纲
这篇教程分为三部分:
-
Step1: 纯C实现的GEMM
这部分主要介绍GEMM的一些基本概念和记号 (A,B,C,m,n,k),并且介绍了实现过程中用到的一些工具函数,在文件
gemm_utils.h中. -
Step2: 调用OpenBLAS的GEMM
这部分调用Openblas库的
cblas_sgemm函数,并比较了openblas和纯C实习的矩阵乘法在 3399上单核A53的性能,并比较了两种实现的输出结果。 -
Step3: Tengine中的GEMM
这部分介绍了Tengine中用到的GEMM的4X16 kernel实现。
运行这个教程的代码,你需要:
- 可以执行armv8汇编的环境,比如RK3399
- linux操作系统: 本教程的编译脚本使用的是Makefile (其他操作系统读者可自行写编译脚本)
Step1: GEMM with Pure C Code
我们首先执行 step1部分的代码,看看程序输出结果,然后我们再解释这部分的具体实现。
到step1目录下,直接make,然后运行测试程序
cd step1
make
./test
可以看到输出结果为:
A=
3.000000 2.000000 1.000000 3.000000
1.000000 3.000000 2.000000 0.000000
1.000000 1.000000 2.000000 3.000000
2.000000 3.000000 3.000000 2.000000
================
B=
3.000000 2.000000 1.000000 3.000000
1.000000 3.000000 2.000000 0.000000
1.000000 1.000000 2.000000 3.000000
2.000000 3.000000 3.000000 2.000000
================
C=
18.000000 22.000000 18.000000 18.000000
8.000000 13.000000 11.000000 9.000000
12.000000 16.000000 16.000000 15.000000
16.000000 22.000000 20.000000 19.000000
================
这个程序中我们计算的矩阵乘法是 A(m,k) * B(k,n) =C(m,n):
- A 是第一个输入矩阵
- m 是矩阵A的行数
- k 是矩阵A的列数
- B 是第二个输入矩阵
- k 是矩阵B的行数
- n 是矩阵B的列数
- C 是输出矩阵
- m 是矩阵C的行数
- n 是矩阵C的列数
我们调用头文件 gemm_utils.h中的初始化函数init来为三个矩阵申请内存并初始化:
float* A = init(m*k,3);
float* B = init(n*k,3);
float* C = init(m*n,0);
矩阵乘法的纯C实现如下:
void gemm_pure_c(float* A, float* B, float* C,int m,int n,int k)
{
for(int i=0;i调用这个函数
gemm_pure_c(A,B,C,m,n,k);
打印出A,B,C三个矩阵的元素.:
printf("A=\n");printM(A,m,k);
printf("B=\n");printM(B,k,n);
printf("C=\n");printM(C,m,n);
你可以根据A,B矩阵的值,手算出矩阵C的结果,然后再和程序的结果进行比较,看看结果是否一致。
Step2: GEMM with OpenBLAS
什么是OpenBLAS?
OpenBLAS 是一个开源的基础线性代数计算库,BLAS的英文全称是Basic Linear Algebra Subprograms。它在不同的处理器上都做了优化。
如何安装OpenBLAS?
在Linux上,可以直接通过apt-get安装这个库:
sudo apt-get install libopenblas-dev
如何运行step2代码?
cd step2
make
export OMP_NUM_THREADS=1
taskset 0x1 ./test
可以得到的结果是:
[m n k]: 256 128 256
[openblas]: 4.68 ms
[pure c]: 32.22 ms
[blas VS pure_C]: maxerr=0.000076
这个例子中,我们只看单核心的性能,在RK3399板子上,我们看单个A53的性能
- Openblas是通过OMP来进行多线程加速,我们首先将OMP设置线程数为1:
export OMP_NUM_THREADS=1
- 用
taskset绑定cpu核心(编号为0x1的cpu):taskset 0x1 ./test
从耗时统计上看,计算相同尺寸的矩阵乘法,调用OpenBLAS库的性能明显优于纯C实现。同时我们也计算了这两种实现的输出的结果的误差,以验证实现的正确性。
进行矩阵乘法运算调用的是OpenBLAS库中的 cblas_sgemm,需要包含头文件-lopenblas选项。
#include
void gemm_blas(float* A,float* B,float* C,int m,int n,int k)
{
// C=alpha*A*B+beta*C
int alpha =1;
int beta = 0;
cblas_sgemm(CblasRowMajor,
CblasNoTrans, CblasNoTrans,
m, n, k,
alpha,
A, k,
B, n,
beta,
C, n);
}
在时间统计方面,我们重复计算了50次,取平均时间:
int rep = 50;
struct timeval t0, t1;
gettimeofday(&t0, NULL);
for(int i = 0; i < rep; i++)
gemm_blas(A,B,C1,m,n,k);
gettimeofday(&t1, NULL);
float blas_time = ( float )((t1.tv_sec * 1000000 + t1.tv_usec) - (t0.tv_sec * 1000000 + t0.tv_usec)) / 1000;
printf("[openblas]:\t%.2f ms\n", blas_time / rep);
Step3: GEMM with Tengine 16x4 kernel
我们首先在RK3399上执行这部分代码,看看在RK3399的1A53的性能, 然后我们再详细解释Tengine 4x16 kernel的具体实现。
cd step3
make
export OMP_NUM_THREADS=1
taskset 0x1 ./test
运行完上述命令,可以得到:
[m n k]: 256 256 256
[tengine 4x16]: 7.71 ms
[openblas]: 9.55 ms
[pure c]: 316.00 ms
[blas VS tengine]: maxerr=0.000061
可以看出Tengine 4x16 kernel在这三种实现中获得最好的性能。下面将介绍Tengine 4x16 kernel的具体实现。
这部分教程以 Tengine源码中的 sgemm_4x16_interleave.S 为例子,我们对汇编代码做了一些简化,只支持k是4的倍数的情况。
Interleave
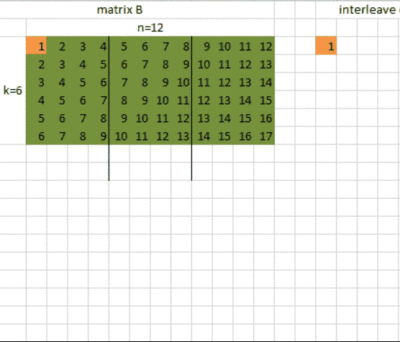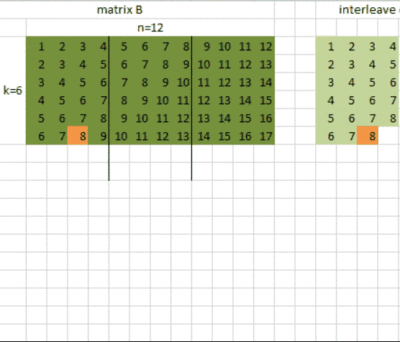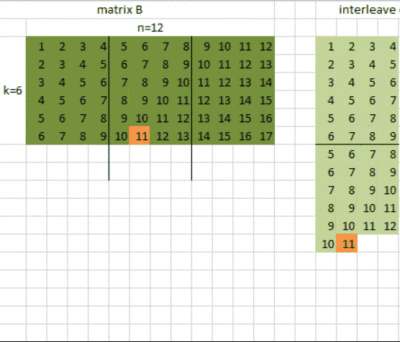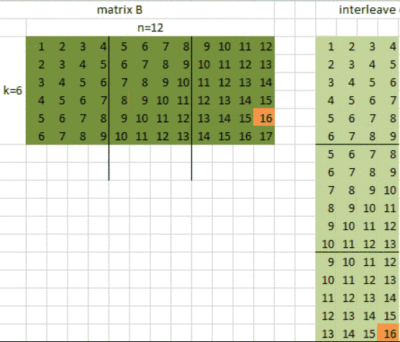
在使用Tengine的4x16 kernel之前, 首先要对矩阵A和矩阵B的数据进行interleave。什么是interleave呢?Interleave叫交错排布,表示对数据进行重新排布,为了在计算读取数据的时候能更好地利用缓存。
Tengine 4x16 kernel中, 我门对矩阵 A的数据是对m中的每16个元素进行重排, 对矩阵B的数据是对n的每4个元素进行重排。
这是矩阵B数据重排的C代码:
void interleave_B4(float* src,float* dst,int n,int k)
{
float* ptr = dst;
for(int i=0;i< n;i+=4)
{
for(int j=0;j下面这个动图展示了矩阵B的数据重排:
这是矩阵A数据重排的C代码:
void interleave_A16(float* src,float* dst,int m,int k)
{
float* ptr = dst;
for(int i=0;i< m;i+=16)
{
for(int j=0;jtengine_4x16_kernel
Tengine的4x16 kernel计算的n=4,m=16的情况,目前支持的k是4的倍数:
A [ 16 , k ] × B [ k , 4 ] = C [ 16 , 4 ] A[16, k] \times B[k,4] = C[16,4] A[16,k]×B[k,4]=C[16,4]
我们在loop4计算k的每四个元素:
- 加载B的数据到寄存器
v0,v1,v2,v3 - 加载A的数据到寄存器
v4,v5,v6,v7,v8,v9,v10,v11
ldr q0, [x1]
ldr q1, [x1, 0x10]
ldp q2, q3, [x1, 0x20]
ldp q4, q5, [x2]
ldp q6, q7, [x2, 0x20]
ldp q8, q9, [x2, 0x40]
ldp q10,q11,[x2, 0x60]
下面的动图演示了4x16的kernel的每条指令是如何进行计算的
把输出数据保存:
stp q16, q17 ,[x0]
stp q18, q19 ,[x0, #0x20]
stp q20, q21 ,[x0, #0x40]
stp q22, q23 ,[x0, #0x60]
stp q24, q25 ,[x0, #0x80]
stp q26, q27 ,[x0, #0xa0]
stp q28, q29 ,[x0, #0xc0]
stp q30, q31 ,[x0, #0xe0]
重新排布输出数据:
for(int i=0;iWhat’s more?
这个教程的代码只是一个示例,part3的代码只支持:
- m 是16的倍数
- n 是4的倍数
- k 是4的倍数
看完这个教程,建议可以尝试以下的一些拓展工作:
- 你可以修改代码来支持任意数值的k,可参考sgemm_4x16_interleave.S这个汇编代码,添加
loop1. - 你可以把
interleave_B4函数替换成汇编,以优化性能。 - 你可以拓展代码,支持任意数值的
mandn - 你可以尝试写一个
4x4_kernel.S的armv8汇编 - 你可以尝试写一个
4x4_kernel.S的armv7汇编