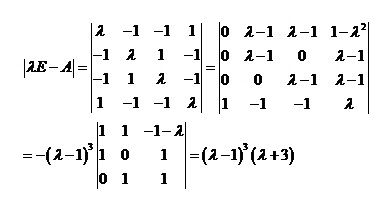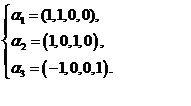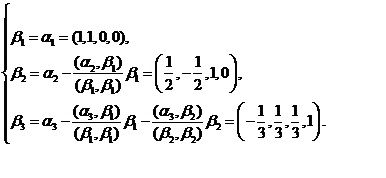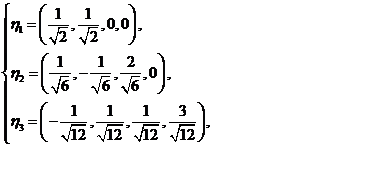矩阵对角化

一、矩阵对角化的理论
一个映射或者一个线性变换，都有一个矩阵和它相对应。矩阵或者映射是不是可以对角化，对工程应用来说比较重要，因为对角化后的矩阵，乘积简单，经过多次变换的话，相当于矩阵的多次方。矩阵能不能对角化，取决于它的特称向量能否构成矩阵的一个基。
1．在域 F 上的 n × n 矩阵 A 是可对角化的，当且仅当它的特征空间的维度等于 n，它为真当且仅当存在由 A 的特征向量组成的Fn的基。如果找到了这样的基，可以形成有基向量作为纵列的矩阵 P，而 P-1AP 将是对角矩阵。这个矩阵的对角元素是 A 的特征值。
2. 线性映射 T : V → V 是可对角化的，当且仅当它的特征空间的维度等于 dim(V)，它为真当且仅当存在由 T 的特征向量组成的 V 的基。T 关于这个基将表示为对角矩阵。这个矩阵的对角元素是 T 的特征值。
另一个特征化: 矩阵或线性映射在域 F 上可对角化的，当且仅当它的极小多项式在 F 上有不同的线性因子。

下列充分(但非必要)条件经常是有用的。
1. n × n 矩阵 A 只在域 F 上可对角化的，如果它在 F 中有 n 个不同的特征值，就是说，如果它的特征多项式在 F 中有 n 个不同的根。
2. 线性映射 T : V → V 带有 n=dim(V) 是可对角化的，如果它有 n 个不同的特征值，就是说它的特征多项式在 F 中有 n 个不同的根。
3. 在域 F 上的 n × n 矩阵 A，如果重根的维数等于其线性无关的特征向量的个数，则矩阵A可以对角化。
4.
二、矩阵对角化过程
下面例子中，矩阵A是对称的，它可以进行对角化，虽然它只有2个不同的特征值，但是有4个线性无关的特征向量，所以能进行对角化。
给定矩阵A，求它的特征值、特征向量，并对它进行对角化。
（1）求特征多项式，matlab命令p= poly(A)；
（2）求解特征多项式，求出特征值，solve（P）；
（3）分别将特征值带入齐次方程组，求出基础解系
（4）针对每个特征值下的基础解系，进行正交化。
（5）对正交化后的向量单位化

例子：已知

求出一正交矩阵 使 成对角形.
解：先求出的 特征值.由

即得的特征值为 （三重）， .
其次，求属于1的特征向量.把 代入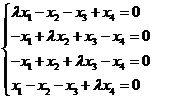
（*）
求得基础解系为

把它们正交化，得

再单位化，得

这是属于三重特征值 三个标准正交的特征向量.
再求属于 的特征向量.用代入（*）式求得其基础解系为 .
把它单位化，得.
特征向量 构成的一组标准正交基，所求的正交矩阵为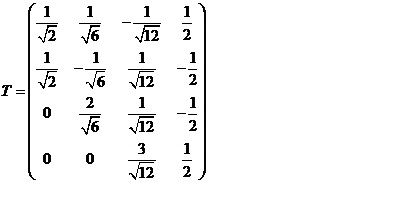
.
而
.
三、matlab实现过程
(1)求特征多项式和特征值

clc
clear all
A=[0 1 1 -1;1 0 -1 1 ;1 -1 0 1;-1 1 1 0]
p=poly(A)
% p = 1.0000 0 -6.0000 8.0000 -3.0000
p1=poly2str(p,’x’)
% p1 = x^4 - 6 x^2 + 8 x - 3
p2=sym(‘x^4 - 6 x^2 + 8 x - 3’) %怎样引用前面的平p1
s1=solve(p2) %查看 s1 =-3
1
1
1
（2）求1的特征向量
B=1*eye(4,4)-A
c=rref(B);

% c =

% 1 -1 -1 1
% 0 0 0 0
% 0 0 0 0
% 0 0 0 0
%相当于 x1-x2-x3+x4=0
%4个未知数，一个方程，有三个自由变量，自行设置 x1=1 ,x2=1,x3=0,de x4=0
x1=1 ,x2=0,x3=1,de x4=0
x1=-1 ,x2=0,x3=0,de x4=1
%得一个基础解系
a1=[1 1 0 0];
a2=[1 0 1 0];
a3=[-1 0 0 1];
%对上面的3个向量正交化
b1=a1;
b2=a2-a2.*b1/sqrt(b1.*b1);
b3=a3-a3.*b1/sqrt(b1.*b1)-a3.*b2/sqrt(b2.*b2);
format rat %分数显示
jie=[b1;b2;b3]’

%jie =

1.0000    0.5000   -0.0000
1.0000   -0.5000    1.0000
     0    0.5000    1.0000
     0   -0.5000    2.0000

jie(abs(jie)<0.0001)=0;
%单位化
format short
d1=jie(:,1)/norm(jie(:,1));
d2=jie(:,2)/norm(jie(:,2));
d3=jie(:,3)/norm(jie(:,3));

format rat %分数显示

D=[d1,d2,d3]
format rat %分数显示
D =

0.7071    0.5000   -0.0000
0.7071   -0.5000    0.4082
     0    0.5000    0.4082
     0   -0.5000    0.8165

% D’*D

ans =

1.0000    0.0000    0.2887
0.0000    1.0000   -0.4082
0.2887   -0.4082    1.0000

这时第1个列向量和第三个列向量内积不为0，有误差，难道前面的正交化过程有误？

尝试改进一下
b1=a1;
b2=a2 -(a2*b1’/(b1*b1’))*b1;
b3=a3-(a3*b1’/ (b1*b1’))*b1-(a3*b2’/ (b2*b2’))*b2;
format rat %分数显示
jie=[b1;b2;b3]’
jie =

1.0000    0.5000   -0.3333
1.0000   -0.5000    0.3333
     0    1.0000    0.3333
     0         0    1.0000

d1=jie(:,1)/norm(jie(:,1));
d2=jie(:,2)/norm(jie(:,2));
d3=jie(:,3)/norm(jie(:,3));
D =

0.7071    0.4082   -0.2887
0.7071   -0.4082    0.2887
     0    0.8165    0.2887
     0         0    0.8660

D’*D

ans =

1.0000         0         0
     0    1.0000   -0.0000
     0   -0.0000    1.0000

（3）求-3的特征向量
B2=(-3)*eye(4,4)-A
C2=rref(B2)

%C2 =

 1     0     0    -1
 0     1     0     1
 0     0     1     1
 0     0     0     0

有1个自由变量，取x1=1 得x4=1;x2=-1;x3=-1;
cc=[1 -1 -1 1]
cc=cc/norm(cc);

(4) T=[D,cc]
(5) T=[D,cc’]

T =

0.7071 0.4082 -0.2887 0.5
0.7071 -0.4082 0.2887 -0.5
0 0.8165 0.2887 -0.5
0 0 0.8660 0.5

T’*A*T
ans =

1.0000         0         0         0
     0    1.0000   -0.0000         0
     0         0    1.0000    0.0000
     0         0         0   -3.0000

三 使用matlab函数分解

clc
clear all
A=[0 1 1 -1;1 0 -1 1 ;1 -1 0 1;-1 1 1 0]

[U,S,V]=svd(A,0)
U =

0.5000         0    0.8660   -0.0000

-0.5000 -0.0000 0.2887 0.8165
-0.5000 0.7071 0.2887 -0.4082
0.5000 0.7071 -0.2887 0.4082

S =

3.0000         0         0         0
     0    1.0000         0         0
     0         0    1.0000         0
     0         0         0    1.0000

% 特征值前面是-3，在这是3；这个影响大不大？
V =

-0.5000 0 0.8660 0
0.5000 0 0.2887 0.8165
0.5000 0.7071 0.2887 -0.4082
-0.5000 0.7071 -0.2887 0.4082

[m,n] = size(A);
if m > 1, s = diag(S);
elseif m == 1, s = S(1);
else s = 0;
end
tol = max(m,n) * max(s) * eps(class(A));
r = sum(s > tol);
Q = U(:,1:r);
Q =

0.5000         0    0.8660   -0.0000

-0.5000 -0.0000 0.2887 0.8165
-0.5000 0.7071 0.2887 -0.4082
0.5000 0.7071 -0.2887 0.4082
Q’*Q

ans =

1.0000         0   -0.0000   -0.0000
     0    1.0000         0   -0.0000

-0.0000 0 1.0000 -0.0000
-0.0000 -0.0000 -0.0000 1.0000
U*S*V’

ans =

0.0000    1.0000    1.0000   -1.0000
1.0000   -0.0000   -1.0000    1.0000
1.0000   -1.0000   -0.0000    1.0000

-1.0000 1.0000 1.0000 -0.0000
U-Q

ans =

 0     0     0     0
 0     0     0     0
 0     0     0     0
 0     0     0     0

Q*S*Q’

ans =

1.5000   -0.5000   -0.5000    0.5000

-0.5000 1.5000 0.5000 -0.5000
-0.5000 0.5000 1.5000 -0.5000
0.5000 -0.5000 -0.5000 1.5000

Q*S*V’

ans =

0.0000    1.0000    1.0000   -1.0000
1.0000   -0.0000   -1.0000    1.0000
1.0000   -1.0000   -0.0000    1.0000

-1.0000 1.0000 1.0000 -0.0000
Q*S*V’= U*S*V’，需要注意的是，U和V虽然十分相似，但符号不同，所以U和V不能互相代替。