基于MATLAB实现ECG心电信号处理
原文出处https://blog.csdn.net/zhaomengszu/article/details/78842613
这是原文的代码,直接复制后无法运行,显示M和TIME没有定义。
需要一个ramat函数把心电数据读取出来。
首先下载心电数据,地址https://www.physionet.org/cgi-bin/atm/ATM
心电数据集下载
图片来源https://blog.csdn.net/qq_24694761/article/details/78677321
然后下载100m.mat和100m.hea即可,一定要下载.hea文件!!!
最后下载rdmat函数读取数据,附上下载链接https://download.csdn.net/download/coppa/11080297
将下载好后的所有文件放在同一文件夹,把以下的代码建立一个新的.m文件,命名为ECG.m
运行ECG.m文件。
clc;
[TIME,M,Fs,siginfo]=rdmat('100m')
%------------------------------低通滤波器滤除肌电信号------------------------------
Fs=1500; %采样频率
fp=80;fs=100; %通带截止频率,阻带截止频率
rp=1.4;rs=1.6; %通带、阻带衰减
wp=2*pi*fp;ws=2*pi*fs;
[n,wn]=buttord(wp,ws,rp,rs,'s'); %'s'是确定巴特沃斯模拟滤波器阶次和3dB
%截止模拟频率
[z,P,k]=buttap(n); %设计归一化巴特沃斯模拟低通滤波器,z为极点,p为零点和k为增益
[bp,ap]=zp2tf(z,P,k) %转换为Ha(p),bp为分子系数,ap为分母系数
[bs,as]=lp2lp(bp,ap,wp) %Ha(p)转换为低通Ha(s)并去归一化,bs为分子系数,as为分母系数
[hs,ws]=freqs(bs,as); %模拟滤波器的幅频响应
[bz,az]=bilinear(bs,as,Fs); %对模拟滤波器双线性变换
[h1,w1]=freqz(bz,az); %数字滤波器的幅频响应
m=filter(bz,az,M(:,1));
figure
freqz(bz,az);title('巴特沃斯低通滤波器幅频曲线');
figure
subplot(2,1,1);
plot(TIME,M(:,1));
xlabel('t(s)');ylabel('mv');title('原始心电信号波形');grid;
subplot(2,1,2);
plot(TIME,m);
xlabel('t(s)');ylabel('mv');title('低通滤波后的时域图形');grid;
N=512
n=0:N-1;
mf=fft(M(:,1),N); %进行频谱变换(傅里叶变换)
mag=abs(mf);
f=(0:length(mf)-1)*Fs/length(mf); %进行频率变换
figure
subplot(2,1,1)
plot(f,mag);axis([0,1500,1,50]);grid; %画出频谱图
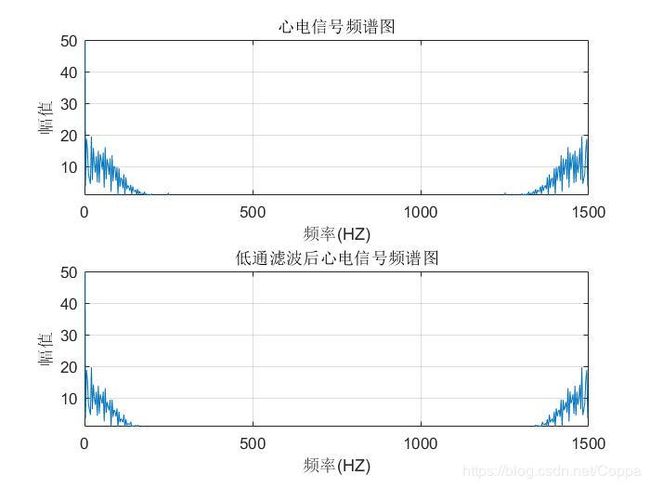
xlabel('频率(HZ)');ylabel('幅值');title('心电信号频谱图');
mfa=fft(m,N); %进行频谱变换(傅里叶变换)
maga=abs(mfa);
fa=(0:length(mfa)-1)*Fs/length(mfa); %进行频率变换
subplot(2,1,2)
plot(fa,maga);axis([0,1500,1,50]);grid; %画出频谱图
xlabel('频率(HZ)');ylabel('幅值');title('低通滤波后心电信号频谱图');
wn=M(:,1);
P=10*log10(abs(fft(wn).^2)/N);
f=(0:length(P)-1)/length(P);
figure
plot(f,P);grid
xlabel('归一化频率');ylabel('功率(dB)');title('心电信号的功率谱');
%-----------------带陷滤波器抑制工频干扰-------------------
%50Hz陷波器:由一个低通滤波器加上一个高通滤波器组成
%而高通滤波器由一个全通滤波器减去一个低通滤波器构成
Me=100; %滤波器阶数
L=100; %窗口长度
beta=100; %衰减系数
Fs=1500;
wc1=49/Fs*pi; %wc1为高通滤波器截止频率,对应51Hz
wc2=51/Fs*pi ;%wc2为低通滤波器截止频率,对应49Hz
h=ideal_lp(0.132*pi,Me)-ideal_lp(wc1,Me)+ideal_lp(wc2,Me); %h为陷波器冲击响应
w=kaiser(L,beta);
y=h.*rot90(w); %y为50Hz陷波器冲击响应序列
m2=filter(y,1,m);
figure
subplot(2,1,1);plot(abs(h));axis([0 100 0 0.2]);
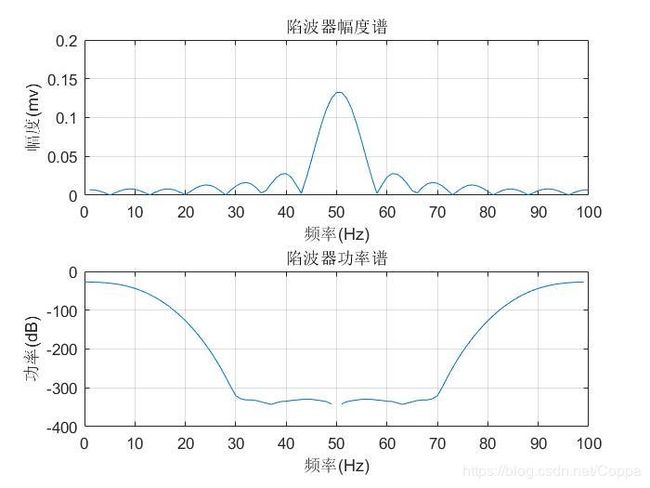
xlabel('频率(Hz)');ylabel('幅度(mv)');title('陷波器幅度谱');grid;
N=512;
P=10*log10(abs(fft(y).^2)/N);
f=(0:length(P)-1);
subplot(2,1,2);plot(f,P);
xlabel('频率(Hz)');ylabel('功率(dB)');title('陷波器功率谱');grid;
figure
subplot (2,1,1); plot(TIME,m);
xlabel('t(s)');ylabel('幅值');title('原始信号');grid;
subplot(2,1,2);plot(TIME,m2);
xlabel('t(s)');ylabel('幅值');title('带阻滤波后信号');grid;
figure
N=512
subplot(2,1,1);plot(abs(fft(m))*2/N);axis([0 100 0 1]);
xlabel('t(s)');ylabel('幅值');title('原始信号频谱');grid;
subplot(2,1,2);plot(abs(fft(m2))*2/N);axis([0 100 0 1]);
xlabel('t(s)');ylabel('幅值');title('带阻滤波后信号频谱');grid;
%其中,ideal_lp()函数在另一个M文件中,具体如下:
%理想低通滤波器
%截止角频率wc,阶数Me
function hd=ideal_lp(wc,Me)
alpha=(Me-1)/2;
n=[0:Me-1];
p=n-alpha+eps; %eps为很小的数,避免被0除
hd=sin(wc*p)./(pi*p); %用Sin函数产生冲击响应
%------------------IIR零相移数字滤波器纠正基线漂移-------------------
Wp=1.4*2/Fs; %通带截止频率
Ws=0.6*2/Fs; %阻带截止频率
devel=0.005; %通带纹波
Rp=20*log10((1+devel)/(1-devel)); %通带纹波系数
Rs=20; %阻带衰减
[N Wn]=ellipord(Wp,Ws,Rp,Rs,'s'); %求椭圆滤波器的阶次
[b a]=ellip(N,Rp,Rs,Wn,'high'); %求椭圆滤波器的系数
[hw,w]=freqz(b,a,512);
result =filter(b,a,m2);
figure
freqz(b,a);
figure
subplot(211); plot(TIME,m2);
xlabel('t(s)');ylabel('幅值');title('原始信号');grid
subplot(212); plot(TIME,result);
xlabel('t(s)');ylabel('幅值');title('线性滤波后信号');grid
figure
N=512;
subplot(2,1,1);plot(abs(fft(m2))*2/N);
xlabel('频率(Hz)');ylabel('幅值');title('原始信号频谱');grid;
subplot(2,1,2);plot(abs(fft(result))*2/N);
xlabel('频率(Hz)');ylabel('幅值');title('线性滤波后');grid;
subplot(2,1,2);plot(abs(fft(result))*2/N);
xlabel('线性滤波后信号频谱');ylabel('幅值');grid;
end
以上程序的结果如下:
图1 图2
图3 图4
图1是所设计的巴特沃斯数字低通滤波器的幅频响应曲线,图1是在时域滤波前后心电信号的波形图,图3是在频域滤波前后心电信号的频谱图,图4是心电信号的功率谱图。图形的密集程度与所选的数据集大小有关,例如我选的数据集大小为1分钟,共60s。
(2)工频干扰的抑制
%—————–带陷滤波器抑制工频干扰——————-
%50Hz陷波器:由一个低通滤波器加上一个高通滤波器组成
%而高通滤波器由一个全通滤波器减去一个低通滤波器构成
Me=100; %滤波器阶数
L=100; %窗口长度
beta=100; %衰减系数
Fs=1500;
wc1=49/Fs*pi; %wc1为高通滤波器截止频率,对应51Hz
wc2=51/Fs*pi ;%wc2为低通滤波器截止频率,对应49Hz
h=ideal_lp(0.132*pi,Me)-ideal_lp(wc1,Me)+ideal_lp(wc2,Me); %h为陷波器冲击响应
w=kaiser(L,beta);
y=h.*rot90(w); %y为50Hz陷波器冲击响应序列
m2=filter(y,1,m);
figure
subplot(2,1,1);plot(abs(h));axis([0 100 0 0.2]);
xlabel('频率(Hz)');ylabel('幅度(mv)');title('陷波器幅度谱');grid;
N=512;
P=10*log10(abs(fft(y).^2)/N);
f=(0:length(P)-1);
subplot(2,1,2);plot(f,P);
xlabel('频率(Hz)');ylabel('功率(dB)');title('陷波器功率谱');grid;
figure
subplot (2,1,1); plot(TIME,m);
xlabel('t(s)');ylabel('幅值');title('原始信号');grid;
subplot(2,1,2);plot(TIME,m2);
xlabel('t(s)');ylabel('幅值');title('带阻滤波后信号');grid;
figure
N=512
subplot(2,1,1);plot(abs(fft(m))*2/N);axis([0 100 0 1]);
xlabel('t(s)');ylabel('幅值');title('原始信号频谱');grid;
subplot(2,1,2);plot(abs(fft(m2))*2/N);axis([0 100 0 1]);
xlabel('t(s)');ylabel('幅值');title('带阻滤波后信号频谱');grid;
%其中,ideal_lp()函数在另一个M文件中,具体如下:
%理想低通滤波器
%截止角频率wc,阶数Me
function hd=ideal_lp(wc,Me)
alpha=(Me-1)/2;
n=[0:Me-1];
p=n-alpha+eps; %eps为很小的数,避免被0除
hd=sin(wc*p)./(pi*p); %用Sin函数产生冲击响应
end
以上程序的结果如下:
图5 图6
图7
图5是带陷滤波器的幅度谱和功率谱,从图中可以看到在50Hz处,滤波器的幅度很大,而且功率在-150以下,说明带陷性能较好。图6是在时域滤波前后的心电信号图,可以看出,滤波后波形有了略微的改善。图7是在频域滤波前后的心电信号频谱图。
(3)基线漂移的纠正
%——————IIR零相移数字滤波器纠正基线漂移——————-
Wp=1.4*2/Fs; %通带截止频率
Ws=0.6*2/Fs; %阻带截止频率
devel=0.005; %通带纹波
Rp=20*log10((1+devel)/(1-devel)); %通带纹波系数
Rs=20; %阻带衰减
[N Wn]=ellipord(Wp,Ws,Rp,Rs,'s'); %求椭圆滤波器的阶次
[b a]=ellip(N,Rp,Rs,Wn,'high'); %求椭圆滤波器的系数
[hw,w]=freqz(b,a,512);
result =filter(b,a,m2);
figure
freqz(b,a);
figure
subplot(211); plot(TIME,m2);
xlabel('t(s)');ylabel('幅值');title('原始信号');grid
subplot(212); plot(TIME,result);
xlabel('t(s)');ylabel('幅值');title('线性滤波后信号');grid
figure
N=512
subplot(2,1,1);plot(abs(fft(m2))*2/N);
xlabel('频率(Hz)');ylabel('幅值');title('原始信号频谱');grid;
subplot(2,1,2);plot(abs(fft(result))*2/N);
xlabel('频率(Hz)');ylabel('幅值');title('线性滤波后');grid;s
ubplot(2,1,2);plot(abs(fft(result))*2/N);
xlabel('线性滤波后信号频谱');ylabel('幅值');grid; 以上程序的结果:
图8 图9
图8是在时域滤波前后的心电信号图,可以看出,滤波后基线漂移得到了改善,图9是在频域滤波前后的心电信号频谱图。