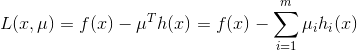最优化问题的分类，拉格朗日乘子法

一、最优化问题的分类

最优化问题可以分为一下三类：

<1>无约束的优化问题，可以写成：

       

对于第<1>类的优化问题，常常使用的方法就是Fermat定理，即使用求取f(x)的导数，然后令其为零，可以求得候选最优值，再在这些候选值中验证；如果是凸函数，可以保证是最优解。

<2>有等式约束的优化问题，可以写成：

　　

　　约束条件  

对于第<2>类的优化问题，常常使用的方法就是拉格朗日乘子法（Lagrange Multiplier) ，即把等式约束  用一个系数与目标函数f(x)写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。拉格朗日函数的形式如下，u即拉格朗日乘子：

　　

通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。

<3>有不等式约束的优化问题，可以写成：

　　

　　约束条件  

　　　　　　　　　

对于第<3>类的优化问题，常常使用的方法就是KKT条件。同样地，我们把所有的等式、不等式约束与f(x)写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。

 

二、拉格朗日乘子法（Lagrange Multiplier）：

 拉格朗日乘子法可以应用于有等式约束的优化问题和有不等式约束的优化问题，

对于有等式约束的优化问题， ，约束条件   ，其中 f(x) 被称为目标函数

<1>当没有约束条件的时候，我们通过求导的方法，来寻找最优点

设  是这个最优点，即此时有

　　 

此外，如果 f(x) 是一个实值函数， 是一个n维向量的话，那么 f(x) 对向量  的导数被定义为

　　

 

<2>当有一个等式约束条件  的时候，举例设

　　

　　

从几何的角度看，可以看成是在一个曲面  上寻找函数  的最小值

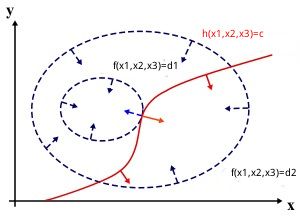
设目标函数  ，当 z 取不同的值的时候，相当于可以投影在曲面 上，即形成等高线，如下图

当  取d1或者d2的时候，形成了虚线的等高线，此时我们要求的是最小的z

现在我们约束  的时候，在曲面 上形成一条曲线，即图中红色的曲线

假设形成的红色曲线与等高线相交，交点就是同时满足等式约束条件和目标函数的可行域的值，但肯定不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小。

只有到等高线与目标函数的曲线相切的时候，可能取得最优值，如上图中的情况，即等高线和目标函数的曲线在该点的法向量必须有相同方向，所以最优值必须满足：f(x)的梯度 =  * h(x)的梯度，  是常数，表示左右两边同向。这个等式就是拉格朗日函数  对参数x求导后，令其等于0的结果，即，最后求得最优解是  。

 

以上的约束条件只是 ，这时约束条件是一个等式。

<3>那么当约束条件是多个等式的时候，拉格朗日函数应该改写成

 ，是需要求其最小值的目标函数，是拉格朗日乘子，是约束条件

 

<4>如果约束条件是等式和不等式，且有多个的时候，就需要若干个KKT(Karush-Kuhn-Tucker)条件，即对于

　　

　　约束条件  

　　　　　　　　　

想取得最优解，要满足以下条件（KKT条件）：

　　1. L(x, a, b)对x求导为零；

　　2. h(x) =0;

　　3. a*g(x) = 0;

 

一步步来说明，此时我们要求f(x)的最小值，可以构建拉格朗日函数

　　

为什么这么构建呢？因为当 g(x)<=0，h(x)=0，a>=0 的时候，（注意此处的h(x)=0是KKT条件的第2个）

a*g(x)<=0，所以  在取得最大值的时候，即a*g(x)=0的时候，就等于f(x)，（注意此处的a*g(x)=0是KKT条件的第3个）

所以需要求解的目标函数的最小值写成表达式是

　　

上式的对偶表达式是

　　

由于我们要求的最优化是满足强对偶的，即对偶式子的最优值等于原式子的最优解

设当  的时候有最优解，此时

　　

　　　　　

　　　　　

即函数  在  处取得最小值

用fermat定理，对于函数  求取导数后令其等于0后的结果，（注意此处的导数=0是KKT条件的第1个）

即f(x)的梯度 + a*g(x)的梯度 + b*h(x)的梯度 = 0

 

所以对于多个不等式和等式混合的约束条件的时候，拉格朗日函数可以写成

　　

　　约束条件