数据结构基础21：堆

前言：堆是实现优先级队列效率很高的数据结构，堆其实是一颗特殊的完全二叉树，用下标从1开始的数组表示最有效率。在JVM中，堆是用来存储对象实例以及数组值的区域，可以认为Java中所有通过new创建的对象的内存都在此分配。堆是所有线程共享的，因此在其上进行对象内存的分配均需要进行加锁，这也导致new对象的开销比较大。

栈：内存空间小一些，栈的内存要远远小于堆内存，如果你使用递归的话，那么你的栈很快就会充满。如果递归没有及时跳出，很可能发生StackOverFlowError问题。主要存放函数体的地址、函数的参数、局部变量临时变量等。

堆：内存空间大一些，主要存放一些通过new出来的对象或者malloc申请的内存空间。

一.优先级队列

1、优先级队列(priority queue)是0个或多个元素的集合，每个元素都有一个优先级或权。与FIFO结构的队列不同，在优先级队列中，元素出队列的顺序是由元素的优先级决定的。可以按优先级的递增顺序，也可以按优先级的递减顺序，但不是队列进入队列的顺序。

优先级队列允许的三种操作：

1）Insert

2）findMax或findMin，查找到优先级最大或最小的元素后返回

3)DeleteMax或DeleteMin，删除一个优先级最大或最小元素

在最小优先级队列中，查找和删除的都是优先级最小的元素；在最大优先级队列中，查找和删除的都是优先级最大的元素。优先级队列的元素可以有相同的优先级，对这样的元素，查找和删除可以按任意顺序处理。

2、几种实现

1）使用链表
可以使用一个简单链表，在表头以O(1)执行插入操作，并遍历该链表以删除最大/小元素，需要O(N)。
始终让表保持有序状态，这使得插入代价O(N)，而DeleteMin为O(1)

2）使用二叉查找树
三种操作的平均时间都是O(lgN)
但是二叉查找树支持许多并不需要的操作。而且较二叉堆的数组表示，每个节点会多出两个额外的指针域内存空间用来指向孩子节点，所以空间复杂度略大。还有在最坏情况下的操作时间复杂度可能在O(n)。

3）使用二叉堆
不需要使用指针，以最坏情形O(lgN)支持上述三种操作。

总结：较之于队列，优先级队列的不同在于它每一次取值取的是队列中的最大（小）值，可以用链表和二叉树来实现，然而用链表会使他的时间复杂度变大，所以优先用二叉树来表示优先队列，这种优先级队列就叫“堆”。

二、堆的定义和存储

1、堆的定义

堆是一种特殊的树，一个堆需要满足如下两个条件：

• 一个堆是一个完全二叉树；

• 堆中每个节点的值都必须大于等于或者小于等于其子树中的每个节点。

第一条，完全二叉树要求，除了最后一层，其它层的节点个数都是满的，并且最后一层的节点都靠左排列。

第二条，也等价于，每个节点的值大于等于或者小于等于其左右子节点的值。

按照数据的排列方式可以分为两种：最大堆（大根堆）和最小堆（小根堆）。节点值大于等于其子树中每个节点值的堆称为 “大根堆”，节点值小于等于其子树中每个节点值的堆称为 “小根堆”。

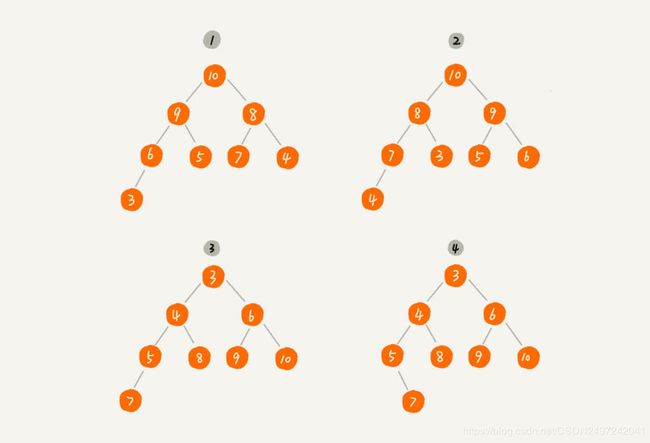图片转自前辈博客

 

上图中，第 1 个和第 2 个是大顶堆，第 3 个是小顶堆，第 4 个不是堆。而且，可以看到，对于同一组数据，我们可以构建多种不同形态的堆。

2、堆的存储

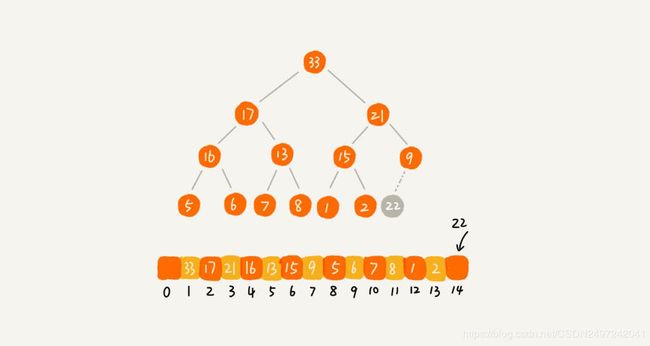
之前我们知道，完全二叉树比较适合用数组来存储，这样非常节省空间，因为不需要额外的空间来存储左右子节点的指针，单纯通过下标我们就可以找到一个节点的左右子节点。故二叉堆一般用数组来表示，这种基于1的数组存储方式便于寻找父节点和子节点。

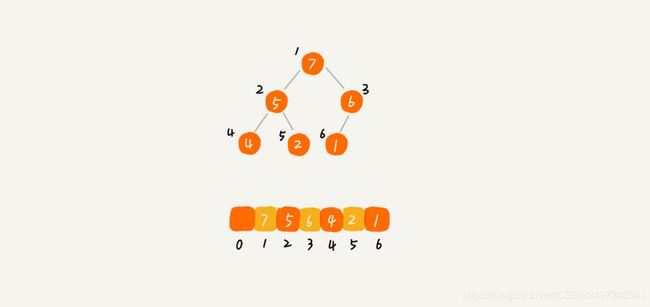图片转自前辈博客

 

可以看到，下标为 的节点的左子节点下标为 ，右子节点下标为 ，而父节点下标就为 取下整。

 

三、堆的插入、查找和删除操作

这里以最大堆的Java实现作为例子。

1、往堆中插入一个元素

往堆中插入一个元素后，我们需要继续保持堆满足它的两个特性。

如果我们将新插入的元素放到堆的最后，此时，这依旧还是一棵完全二叉树，但就是节点的大小关系不满足堆的要求。因此，我们需要对节点进行调整，使之满足堆的第二个特性，这个过程称为堆化（heapify）。

堆化非常简单，就是顺着节点所在的路径，向上或者向下，对比然后交换。

我们从新插入的节点开始，依次与其父结点进行比较，如果不满足子节点值小于等于父节点值，我们就互换两个节点，直到满足条件为止。这个过程是自下向上的，称为从下往上的堆化方法。

Java代码：

/*
 * 最大堆
 */

public class maxHeap19 
{
  private int[] heap; // 数组，从下标 1开始存储数据
  private int n;  // 数组heap的容量
  private int heapSize; //堆的元素个数

  public void maxHeap19(int capicity)
 {
    heap = new int[capicity + 1];
    n = capicity;
    heapSize = 0;
  }
  
  private void swap(int[] nums,int i,int j)
  {
	  int temp = nums[i];
	  nums[i] = nums[j];
	  nums[j] = temp;
  }

  /*
   * 1、大根堆的插入
   */
  public void insert(int data) 
  {
	//堆满了，这里其实可以增加数组长度
    if(heapSize>= n) 
    	return; 
    
    //为元素data寻找插入位置
    int i = ++heapSize;
    heap[i] = data;
    while (i!=1 && heap[i] > heap[i/2]) 
    { // 自下往上堆化
      swap(heap, i, i/2); // swap()函数作用：交换数组中下标为 i和 i/2 的两个元素
      i = i/2;
    }
  }
  
}

2、在堆中查找一个最大/最小元素

  /*
   * 2、查找最大元素
   */
  public int getMax()
  {
     return heap[1];
  }

3、删除堆中最大/最小元素

假设我们构建的是大根堆，那么堆顶元素就是最大值。当我们删除堆顶元素后，就需要把第二大元素放到堆顶，而第二大元素肯定是其左右子节点中的一个。然后，我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。

但是，这个方法有点问题，删除堆顶元素后堆就不满足完全二叉树的条件了。

实际上，我们稍微改变一下思路，就可以解决这个问题。删除堆顶元素后，我们将最后一个结点放到堆顶，然后再依次进行对比，将这个结点交换到正确的位置即可。这个过程是自上而下的，称为从上往下的堆化方法。

Java代码：

/*
   * 3、大根堆的删除
   */
  public int removeMax() 
  {
	  if(heapSize == 0) 
		  return -1; //堆中没有元素
	  
	  heap[1] = heap[++heapSize];//删除堆顶元素后，我们将最后一个元素放到堆顶
	  heapSize--;
	  //重新建堆
	  heapify(heap,heapSize,1);
          return 1;
  }

  private void heapify(int[] a, int n, int i) 
  { // 自上往下堆化
	  while(true) 
	  {
	    int maxPos = i;
	    if (i*2 <= n && a[i] < a[i*2]) 
	    	maxPos = i*2;

	    //如果右孩子比左孩子大
	    if (i*2+1 <= n && a[maxPos] < a[i*2+1])
	    	maxPos = i*2+1;
	    
	    //根节点比左右孩子节点都大
	    if (maxPos == i) 
	    	break;

	    swap(a, i, maxPos);
	    i = maxPos;
	  }
   }

总结：一棵包含 个节点的完全二叉树，树的高度不会超过 。而堆化的过程是顺着结点所在的路径进行比较交换的，所以堆化的时间复杂度和树的高度成正比，也就是 ，也即往堆中插入和删除元素的时间复杂度都为 。

四、左高树

1、出现原因

堆结构是一种隐式数据结构（implicit data structure），用完全二叉树表示的堆在数组中是隐式存贮的（即没有明确的指针或其他数据能够重构这种结构）。由于没有存贮结构信息，这种描述方法空间利用率很高，事实上没有空间浪费。尽管堆结构的时间和空间效率都很高，但它不适合于所有优先队列的应用，尤其是当需要合并两个优先队列或多个长度不同的队列时。因此需要借助于其他数据结构来实现这类应用，左高树（leftist tree）就能满足这种要求。

2、扩充二叉树

扩充二叉树是二叉树中的一种，是指在二叉树中出现空子树的位置增加空树叶，所形成的二叉树。它有一类特殊的节点叫外部节点，用来代替树中的空子树，其余节点叫做内部节点。

增加外部节点的二叉树被称为扩充二叉树。

3、左高树定义和应用

①定义

左高树是一棵扩充二叉树，且如果该二叉树不空，则对其中的每个内部结点x，都有左儿子到一个外部结点的最短路程长度大于或等于右儿子到一个外部结点的最短路程长度。

令s(x)是从节点x到其子树的外部节点的所有路径中最短的一条。根据s(x)的定义，若s(x)是外部节点，则s的值为0；若x为内部节点，则s的值为：min｛s(L),s(R)｝+1,其中L和R分别为x的左右孩子。

②应用

左高树的一个应用是合并操作，应用场景是:当某个优先队列的服务器关闭时,就需要将其与另一个正在运行服务器的优先队列合并。如果两个队列的元素总数为n，则一般的堆结构的复杂度为O(n),但是左高树可以达到O(logn)。插入和删除操作都可以通过合并操作来完成。

4、左高树的种类

1）高度优先左高树

当且仅当一棵二叉树的任何一个内部节点，其左孩子的s值大于等于右孩子的s值时，该二叉树为高度优先左高树（height-biased leftist tree, HBLT）。

2）重量优先左高树

当且仅当一棵二叉树的任何一个内部节点，其左孩子的w值大于等于右孩子的w值时，该二叉树为重量优先左高树（weight-biased leftist tree, WBLT）；最大（小）WBLT 即同时又是最大（小）树的WBLT。

3）最小左高树

最小（最大）左高树是一棵左高树，其中的每个内部结点的关键字值不大于（不小于）该结点的儿子结点的关键字值。

对于最小左高树的操作，插入和删除最小元素操作都可以通过合并操作来完成。要把元素x插入到左高树A中，先建立一棵只有一个元素x的最小左高树B，再合并最小左高树A和B。要从一棵非空最小左高树A删除最小元素，则只需合并最小左高树A的左子树和右子树，再把最小左高树的根结点删除。

以下重点介绍最小左高树的合并操作。

假设要合并最小左高树A和B，首先，沿着A和B的最右路径，得到一棵包含A和B所有元素的二叉树（注意：这里只是得到二叉树，而不是最小左高树）。使得该二叉树具有以下性质：所有结点的关键字都不大于其儿子结点关键字。必要时交换结点的左、右子树，将其转化为最小左高树。

合并操作

1、假设合并最小左高树A和B，首先比较两棵树根结点的关键字值，以最小的关键字作为新二叉树的根结点。

2、保留A的左子树不变，将其右子树与最小左高树B合并，合并后的二叉树成为新的A的右子树。

3、把二叉树转换为最小左高树从最后一个修改结点（注意：这里不是最后结点）开始，回溯到最终的树根结点，使得路径上的所有结点满足不等式：shortest（left_child()）>= shortest（right_child()

五、堆的应用

常见应用场景有堆排序、TopN问题和霍夫曼编码。

Java实现哈夫曼编码算法