剑指offer66道练习题汇总——python版(持续更新)
目录
1.二维数组的查找(数组)
2.替换空格(字符串)
3.从尾到头打印链表(链表)
4.重建二叉树(树)
5.二叉树镜像(树)
6.用两个栈实现队列(栈和队列)
7.斐波那契数列(递归和循环)
8.旋转数组的最小数字(查找和排序)
9.跳台阶(递归与循环)
10.变态跳台阶(递归和循环)
11.单、双链表反转
12.矩形覆盖(递归和循环)
13.链表中倒数第k个节点
14.链表中环的入口结点
15.合并两个排序列表
16.顺时针打印数组
17.输入两个链表,找出它们的第一个公共结点。
18.删除排序链表中重复的结点
19.复杂链表的复制。
20.二叉搜索树第k小的结点。
21.二叉搜索树转为排序后的双向链表。
22.按字典序打印出符串中字符的所有排列。
23.找出数组中出现次数超过一半的数字。
24.之字形打印二叉树
25.从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
26.打印和为S的连续正数序列
27.求无序数组最小的k个数
28.二叉树中和为某一个值的路径
29.连续子数组最大和
30.整数中1出现的次数
1.二维数组的查找(数组)
# -*- coding:utf-8 -*-
class Solution:
# array 二维列表
'''
由于二维列表存在规律:每一行从左到右数值增加,每一列从上到下数值增加。
将target与列表左下角元素比较,若target大于该元素,用于比较的元素的右移;若target小于该元素的话,用于比较的元素上移。
也可以从右上角元素开始比较,道理相似。
'''
def Find(self, target, array):
if len(array)==0:
return False
col=len(array[0])
row=len(array)
j=0
i=row-1
while j<=col-1 and i>=0:
if(target==array[i][j]):
return True
break #如果找到target,就应跳出循环
elif(target2.替换空格(字符串)
# -*- coding:utf-8 -*-
class Solution:
'''
1.从前到后扫描s,用space_num记录空格的个数
2.计算新的列表长度并创建新列表(即new_s)
3.从后到前扫描原字符串s,进行替换,并将结果保存在new_s中
'''
def replaceSpace(self, s):
# write code here
s_len=len(s)
space_num=0
for i in range(s_len):
if s[i]==" ":
space_num+=1
new_len=s_len+space_num*2
new_s=[None for i in range(new_len)]
for i in range(s_len-1,-1,-1):
if (s[i]!=" "):
new_s[i+space_num*2]=s[i]
else:
new_s[i+space_num*2]='0'
new_s[i+space_num*2-1]='2'
new_s[i+space_num*2-2]='%'
space_num-=1
return "".join(new_s)3.从尾到头打印链表(链表)
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
'''数组翻转'''
class Solution:
# 返回从尾部到头部的列表值序列,例如[1,2,3]
def printListFromTailToHead(self, listNode):
list=[]
if listNode==None:
return list
while listNode:
list.append(listNode.val)
listNode=listNode.next
return list[::-1]
'''递归实现'''
class Solution1:
# 返回从尾部到头部的列表值序列,例如[1,2,3]
def printListFromTailToHead(self, listNode):
if listNode == None:
return []
return self.printListFromTailToHead(listNode.next) + [listNode.val]
4.重建二叉树(树)
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回构造的TreeNode根节点
'''
1.创建根节点
2.根据前序遍历中第一个值(即为根节点的值)找到根节点在中序遍历中的位置pos
3.根据规律找到左子树和右子树所对应的前序遍历与中序遍历的列表范围,递归建树。
'''
def reConstructBinaryTree(self, pre, tin):
# write code here
if(len(pre)==0):
return None
if(len(pre)==1):
return TreeNode(pre[0])
else:
root=TreeNode(pre[0])
pos=tin.index(root.val)
root.left=self.reConstructBinaryTree(pre[1:pos+1],tin[0:pos])#数组上界不包括该值
root.right=self.reConstructBinaryTree(pre[pos+1:],tin[pos+1:])
return root5.二叉树镜像(树)
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回镜像树的根节点
'''
根节点左右节点翻转,左右节点所对应的子树也需要翻转,递归实现
'''
def Mirror(self, root):
if root !=None:
root.left,root.right = root.right,root.left
self.Mirror(root.left)
self.Mirror(root.right)
6.用两个栈实现队列(栈和队列)
# -*- coding:utf-8 -*-
'''
A是入栈的,B是出栈的,入栈时,直接进入A即可,出栈时,先判断是否有元素,
如果B没有元素,pop肯定报错,应该先将A中所有的元素压倒B里面,再pop最上面一个元素,如果B中有就直接pop出,就可以,
这是最优的思路,两个栈实现了先进后出,在一起又实现了队列的先进先出。
'''
class Solution:
# 初始化两个栈
def __init__(self):
self.stackA = []
self.stackB = []
# 这里只要求实现队列的push和pop操作,分别使用两个栈表示弹出和压入
def push(self, node):
# write code here
self.stackA.append(node)
def pop(self):
if not self.stackB:
while self.stackA:
self.stackB.append(self.stackA.pop())
return self.stackB.pop()7.斐波那契数列(递归和循环)
# -*- coding:utf-8 -*-
class Solution:
def Fibonacci(self, n):
# write code here
x, y = 0, 1
if n==0:
return 0
if n==1:
return 1
while(n>1):
x,y,n = y, x+y, n - 1
return y8.旋转数组的最小数字(查找和排序)
class Solution:
'''
比较方法:当出现前一个元素的值大于后一个元素的值时,找到分界点,旋转数组最小值为后一个元素的值。
如果是完全旋转(12345旋转后还是12345),数组的第一个值即为旋转数组后的最小值。
'''
def minNumberInRotateArray(self, rotateArray):
r_len=len(rotateArray)
if (r_len)==0:
return 0
else:
for i in range(r_len-1):
if rotateArray[i]>rotateArray[i+1]:
return rotateArray[i+1]
return rotateArray[0]
class Solution:
'''
二分查找:left,right为两个指针,初始时left指向0,right指向len-1;
如果中间元素大于left指针所指向的值,则旋转数组的最小值在中间元素的右边,使left指向中间元素;
如果中间元素小于left指针所指向的值,则旋转数组的最小值在中间元素的左边,使right指向中间元素。
这样,left指针始终指向前一个递增序列,right指针始终指向后一个递增序列。
当right-left=1时,找到最小值,即为right所对应的元素。
'''
def minNumberInRotateArray(self, rotateArray):
left=0
right=len(rotateArray)-1
mid=0
if len(rotateArray)==0:
return 0
else:
while(rotateArray[left]>=rotateArray[right]):
if right-left==1:
mid=right
break
mid=left+(right-left)//2
if (rotateArray[mid]>=rotateArray[left]):
left=mid
elif(rotateArray[mid]<=rotateArray[left]):
right=mid
return rotateArray[mid] 9.跳台阶(递归与循环)
# -*- coding:utf-8 -*-
class Solution:
'''
此问题转化为斐波那契数列
对于第n个台阶来说,只能从n-1或者n-2的台阶跳上来,所以F(n) = F(n-1) + F(n-2)
初始条件 n=1:只能一种方法 n=2:两种
'''
def jumpFloor(self, number):
x,y=1,2
if number==1:
return 1
if number==2:
return 2
while (number>2):
x,y,number=y,x+y,number-1
return y
10.变态跳台阶(递归和循环)
# -*- coding:utf-8 -*-
class Solution:
'''
思路1:可以按照跳台阶问题的思路去思考:
f(n)=f(n-1)+f(n-2)+...+f(n-(n-1))+f(n-n)
f(n-1)=f(n-2)+f(n-3)+...+f(n-1-(n-2))+f(n-1-(n-1))
f(0)=1,表示一次跳n阶,只有一种跳法。
两式相减,可得f(n)=2*f(n-1),最后可得规律f(n)=2^(n-1)
思路2:青蛙从0要到达第n个台阶,最后一个台阶青蛙必定要踩,而中间的1到n-1个台阶,每个台阶青蛙都有踩和不踩两种选择,那么就会有2^(n-1)种可能,即2^(n-1)种跳法。
'''
def jumpFloorII(self, number):
if(number>0):
return 2**(number-1)11.单、双链表反转
双链表的非递归反转与单链表类似,多了一步,将节点的prev指针指向next
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
'''
递归实现
'''
# 返回ListNode
def ReverseList(self, pHead):
if pHead==None or pHead.next==None:
return pHead
reversenode=self.ReverseList(pHead.next)#始终指向要反转的节点,pHead指向反转前一节点
pHead.next.next=pHead
pHead.next=None
return reversenode
class Solution1:
# 返回ListNode
'''
循环实现
'''
def ReverseList(self, pHead):
if pHead==None:
return pHead
cur=pHead
pre=None
pnext=None
while(cur!=None):
pnext=cur.next
cur.next=pre
pre=cur
cur=pnext
return pre12.矩形覆盖(递归和循环)
# -*- coding:utf-8 -*-
class Solution:
def rectCover(self, number):
if number<=0:
return 0
if number==1:
return 1
if number==2:
return 2
x,y=1,2
while(number>2):
x,y,number=y,x+y,number-1
return y13.链表中倒数第k个节点
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
'''
设置两个指针:快指针(fast)、慢指针(low),让快指针先走k-1步,而后两指针一起移动,当快指针到链表末尾时,慢指针指向倒数第k个节点。
注意:链表为空或k=0会返回None;还需要考虑k超过链表长度的情况
'''
def FindKthToTail(self, head, k):
# write code here
if head==None or k<=0:
return None
fast=head
low=head
i=1
while i14.链表中环的入口结点
一个链表中包含环,请找出该链表的环的入口结点。
此问题包含两个步骤:
(1)判断链表中是否有环
选择快慢指针,让快指针每次走两步,慢指针每次走一步,若是单链表中有环的话,那么两个指针会相遇,即指向的节点相同来判断。
当相遇的时候,慢指针在环中走了k步,设环之外的部分长为x,环的长度为n,则快指针一共走了 x+m*n步,(m为快指针在环中走的圈数),慢指针一共走了x+k步,因为快指针的速度是慢指针的两倍。那么可以得到2(x+k)=x+m*n+k;得到x为m*n-k ,慢指针在圈中还剩下的步数n-k;
(2)找到环的入口结点
让快指针从头开始,两个指针每次都走一步,当快指针走了想x(m*n-k)步的时候,到达环的入口,慢指针在圈中走m-1圈加n-k步的时候,也到达环入口那个节点,两个指针再次相遇,此刻的节点就是环的入口的节点。
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
if pHead==None or pHead.next==None:
return None
pFast=pHead
pLow=pHead
while pFast!=None and pFast.next!=None:
pFast=pFast.next.next
pLow=pLow.next
if pLow==pFast:
pFast=pHead
while pFast!=pLow:
pLow=pLow.next
pFast=pFast.next
return pFast
return None15.合并两个排序列表
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
'''
非递归实现
'''
# 返回合并后列表
def Merge(self, pHead1, pHead2):
# write code here
Head=ListNode(0)
tmp=Head
while pHead1!=None and pHead2!=None:
if pHead1.val<=pHead2.val:
tmp.next=pHead1
pHead1=pHead1.next
else:
tmp.next=pHead2
pHead2=pHead2.next
tmp=tmp.next
if pHead1!=None:
tmp.next=pHead1
elif pHead2!=None:
tmp.next=pHead2
return Head.next
class Solution1:
'''
递归实现
'''
# 返回合并后列表
def Merge(self, pHead1, pHead2):
# write code here
if pHead1==None:
return pHead2
if pHead2==None:
return pHead1
tmp=ListNode(0)
if pHead1.val<=pHead2.val:
tmp=pHead1
tmp.next=self.Merge(pHead1.next,pHead2)
else:
tmp=pHead2
tmp.next=self.Merge(pHead1,pHead2.next)
return tmp
16.顺时针打印数组
# -*- coding:utf-8 -*-
class Solution:
'''
可以模拟魔方逆时针旋转的方法,一直做取出第一行的操作
例如
1 2 3
4 5 6
7 8 9
输出并删除第一行后,再进行一次逆时针旋转,就变成:
6 9
5 8
4 7
继续重复上述操作即可。
'''
# matrix类型为二维列表,需要返回列表
def printMatrix(self, matrix):
# write code here
result = []
while matrix:
result += matrix.pop(0)
if not matrix:
break
matrix = self.turn(matrix)
return result
def turn(self, matrix):
# 逆时针旋转函数
col = len(matrix[0])
newmat = []
for i in range(col, 0, -1):
newmat.append([x[i-1] for x in matrix]) #列表推导式
return newmat17.输入两个链表,找出它们的第一个公共结点。
class Solution:
def FindFirstCommonNode(self, pHead1, pHead2):
'''
公共结点后的值,next都相同
假定 List1长度: a+n List2 长度:b+n, 且 a=b.
'''
# write code here
p1=pHead1
p2=pHead2
while(p1!=p2):
p1=p1.next if p1!=None else pHead2
p2=p2.next if p2!=None else pHead1
return p118.删除排序链表中重复的结点
class Solution:
def deleteDuplication(self, pHead):
# write code here
'''
构造一个头结点,使其next指向头结点。
pre指向当前非重复节点
last向后移动搜索
当有重复节点时:节点重复,last一直后移;当遇到非重复节点时,last后移,pre.next=last,指向当前非重复节点
当无重复节点时:pre指向last,last后移。
'''
if pHead==None or pHead.next==None :
return pHead
Head=ListNode(0)
Head.next=pHead
last=pHead
pre=Head
while (last!=None):
if (last.next!=None and last.val==last.next.val):
while (last.next!=None and last.val==last.next.val):
last=last.next
last=last.next
pre.next=last
else:
pre=pre.next
last=last.next
return Head.next19.复杂链表的复制。
class Solution:
# 返回 RandomListNode
'''
1.复制每个节点,将新节点插入到原节点后面
2.将新节点的random指向旧节点的random.next
3.拆分
'''
def Clone(self, pHead):
# write code here
if pHead==None:
return None
tmpHead=pHead
#添节点
while (tmpHead!=None):
cNode=RandomListNode(tmpHead.label)
cNode.next=tmpHead.next
tmpHead.next=cNode
tmpHead=cNode.next
#新节点random赋值,
#注意1:这一步next值不能改变,链表会被破坏!!!
tranHead=pHead
while (tranHead!=None):#注意2:这里的循环条件!!!
tranHeadNext=tranHead.next
if tranHead.random!=None:#注意3:这里的if条件!!!
tranHeadNext.random=tranHead.random.next
tranHead=tranHeadNext.next
#拆分
pNode=pHead
nHead=pHead.next
while (pNode!=None):#注意4:这里的循环条件!!!
cnNode=pNode.next
pNode.next=cnNode.next
cnNode.next=None if cnNode.next==None else cnNode.next.next
pNode=pNode.next
return nHead20.二叉搜索树第k小的结点。
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
方法一:(这种思路比较常规)
class Solution:
'''
主要思路:1.递归中序遍历。
2.取第k个节点。注意k为0和得到的数组长度小于k的情况。
'''
# 返回对应节点TreeNode
def KthNode(self, pRoot, k):
# write code here
sortArray=self.MiddleArray(pRoot)
if len(sortArray)len(hq)的情况
class Solution(object):
def KthNode(self, root, k):
if k==0 :
return None
self.hq=[]
def visit(root):
if root is None:
return None
visit(root.left)
if len(self.hq) < k: #hq 没装到k个
self.hq.append(root)
visit(root.right)
else:
return None
visit(root)
if len(self.hq) 21.二叉搜索树转为排序后的双向链表。
class Solution:
'''
1.先中序遍历二叉搜索树,加入到列表中。
2.修改链表中节点的指向。
'''
def Convert(self, pRootOfTree):
treeList=self.Traversal(pRootOfTree)
if len(treeList)==0:
return None
for i in range(0,len(treeList)):
if i-1>=0:
treeList[i].left=treeList[i-1]
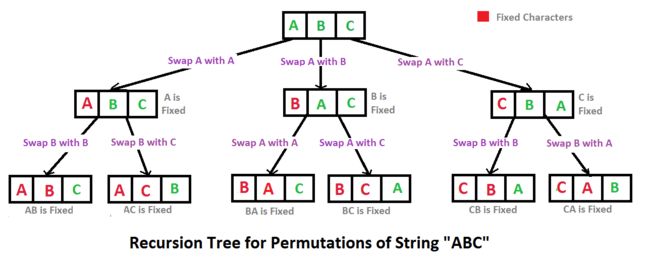
if i+122.按字典序打印出符串中字符的所有排列。
例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
# -*- coding:utf-8 -*-
class Solution:
def __init__(self):
self.AllLists=[]
def Permutation(self, ss):
# write code here
strList=list(ss)
self.SubPermutation(0,len(strList),strList)
return list(sorted(set(self.AllLists)))
def SubPermutation(self,k,n,strList):
if k==n-1:
self.AllLists.append(''.join(strList))
for i in range(k,n):
strList[i],strList[k]=strList[k],strList[i]
self.SubPermutation(k+1,n,strList)
strList[i],strList[k]=strList[k],strList[i]#注意恢复原顺序,以便下次交换23.找出数组中出现次数超过一半的数字。
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
方法一:用了python的内置函数,应该不是面试官想要的。
# -*- coding:utf-8 -*-
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
result=[]
uniqNumber=list(set(numbers))
for i in uniqNumber:
count=numbers.count(i)
if count>len(numbers)/2.0:
return i
break
return 0
方法二:假设有这个数字,那么它的数量一定比其它所有数字之和还要多,按照这个思路得出num,然后验证
原理就是如果确实存在出现次数超过一半的数字,那么他出现的次数一定可以抵消掉没有其他数字出现的次数。当然如果输入的例子不对也可能通过,所以最后需要检查
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
if not numbers:
return 0
num = numbers[0]
count = 1
for i in range(1, len(numbers)):
if numbers[i] == num:
count += 1
else:
count -= 1
if count == 0:
num = numbers[i]
count = 1
count = 0
for i in numbers:
if i == num:
count += 1
return num if count > len(numbers) / 2.0 else 0
方法三:用快排先排序,找到n/2位置的数。24.之字形打印二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def Print(self, pRoot):
# write code here
if not pRoot:
return []
nodeStack=[pRoot]
result=[]
layer=1
while nodeStack:
res = []
nextStack=[]
for i in nodeStack:
res.append(i.val)
if i.left:
nextStack.append(i.left)
if i.right:
nextStack.append(i.right)
nodeStack=nextStack
if layer % 2!=0:
result.append(res)
else:
result.append(res[::-1])
layer+=1
return result25.从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回二维列表[[1,2],[4,5]]
def Print(self, pRoot):
# write code here
if not pRoot:
return []
nodeStack=[pRoot]
result=[]
while nodeStack:
nextStack=[]
res=[]
for node in nodeStack:
res.append(node.val)
if node.left:
nextStack.append(node.left)
if node.right:
nextStack.append(node.right)
nodeStack=nextStack
result.append(res)
return result26.打印和为S的连续正数序列
链接:https://www.nowcoder.com/questionTerminal/c451a3fd84b64cb19485dad758a55ebe
来源:牛客网
1)由于我们要找的是和为S的连续正数序列,因此这个序列是个公差为1的等差数列,而这个序列的中间值代表了平均值的大小。假设序列长度为n,那么这个序列的中间值可以通过(S / n)得到,知道序列的中间值和长度,也就不难求出这段序列了。
2)满足条件的n分两种情况:
n为奇数时,序列中间的数正好是序列的平均值,所以条件为:(n & 1) == 1 && sum % n == 0;
n为偶数时,序列中间两个数的平均值是序列的平均值,而这个平均值(sum/n)的小数部分为0.5,所以条件为:(sum % n) * 2 == n.(被除数是余数的2倍)
3)由题可知n >= 2,那么n的最大值是多少呢?我们完全可以将n从2到S全部遍历一次,但是大部分遍历是不必要的。为了让n尽可能大,我们让序列从1开始,
根据等差数列的求和公式:S = (1 + n) * n / 2,得到.
最后举一个例子,假设输入sum = 100,我们只需遍历n = 13~2的情况(按题意应从大到小遍历),n = 8时,得到序列[9, 10, 11, 12, 13, 14, 15, 16];n = 5时,得到序列[18, 19, 20, 21, 22]。
完整代码:时间复杂度为27
# -*- coding:utf-8 -*-
class Solution:
def FindContinuousSequence(self, tsum):
# write code here
result=[]
maxN=int((2*tsum)**0.5)
for n in range(maxN,1,-1):
if (n&1==1 and tsum % n==0) or (n&1==0 and ((tsum%n)*2==n)):
subResult=[]
for j in range(0,n):
k=(tsum/n)-(n-1)/2+j
subResult.append(k)
result.append(subResult)
return result27.求无序数组最小的k个数
建k个数的最大堆,每次都跟堆顶元素比较
# -*- coding:utf-8 -*-
class Solution:
def swap(self,arr,i,j):
arr[i],arr[j]=arr[j],arr[i]
def build_k_heap(self,arr,k):
for i in range(int(k/2),-1,-1):
self.heapify(arr,i,k)
for i in range(k,len(arr)):
if arr[i]arr[max]:
max=c1
if c2arr[max]:
max=c2
if max!=i:
self.swap(arr,max,i)
self.heapify(arr,max,k)
def GetLeastNumbers_Solution(self, tinput, k):
# write code here
if k>len(tinput) or k<0:
return []
result=self.build_k_heap(tinput,k)
return result 28.二叉树中和为某一个值的路径
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回二维列表,内部每个列表表示找到的路径
def __init__(self):
self.listAll=[]
self.listOne=[]
def FindPath(self, root, expectNumber):
self.FindSubPath(root,expectNumber)
result=sorted(self.listAll,key=len,reverse=True)
return result
def FindSubPath(self,root,expectNumber):
if root==None:
return
self.listOne.append(root.val)
expectNumber-=root.val
if expectNumber==0 and root.left==None and root.right==None:
self.listAll.append(self.listOne[:])
self.FindSubPath(root.left,expectNumber)
self.FindSubPath(root.right,expectNumber)
self.listOne.pop() 29.连续子数组最大和
# -*- coding:utf-8 -*-
class Solution:
'''
maxsum:记录到array[i]的子数组最大和
res:记录所有子数组和的最大值
'''
def FindGreatestSumOfSubArray(self, array):
# write code here
res=array[0]
maxsum=array[0]
for i in range(1,len(array)):
maxsum=max(maxsum+array[i],array[i])
res=max(res,maxsum)
return res30.整数中1出现的次数
# -*- coding:utf-8 -*-
class Solution:
def NumberOf1Between1AndN_Solution(self, n):
# write code here
ones = 0
m=1
while m<=n:
ones += (n / m + 8) / 10 * m + ((n % m + 1) if n / m % 10 == 1 else 0)
m*=10
return ones
31.把数组拍成最小的数
# -*- coding:utf-8 -*-
class Solution:
def PrintMinNumber(self, numbers):
# write code here
if not numbers:
return ""
numbers=list(map(str,numbers))
numbers.sort(cmp=lambda x,y:cmp(x+y,y+x))
return ''.join(numbers)32.第一次只出现一次的字符
# -*- coding:utf-8 -*-
class Solution:
def FirstNotRepeatingChar(self, s):
# write code here
num_dict = {}
for i in range(len(s)):
if s[i] not in num_dict:
num_dict[s[i]] = 1
else:
num_dict[s[i]] += 1
for i in range(len(s)):
if num_dict[s[i]] == 1:
return i
return -133.数字在排序数组中出现的次数
# -*- coding:utf-8 -*-
class Solution:
def GetNumberOfK(self, data, k):
ind = self.midSearch(data, k)
count = 0
if ind != -1:
count = 1
for i in range(ind + 1, len(data)):
if data[i] == k:
count += 1
else:
break
for j in range(ind - 1, -1, -1):
if data[j] == k:
count += 1
else:
break
return count
# write code here
def midSearch(self, data, k):
start = 0
end = len(data) - 1
while start <= end:
mid = (start + end) / 2
if k< data[mid] :
end = mid - 1
elif data[mid] < k:
start = mid + 1
else:
return mid
return -134.二叉树的深度
class Solution:
def TreeDepth(self, pRoot):
# write code here
if pRoot==None:
return 0
count=0
stack=[pRoot]
while stack:
nextStack=[]
for node in stack:
if node.left:
nextStack.append(node.left)
if node.right:
nextStack.append(node.right)
stack=nextStack
count+=1
return count35.判断是否为平衡二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def IsBalanced_Solution(self, pRoot):
# write code here
if not pRoot:
return True
rHeight=self.getDepth(pRoot.right)
lHeight=self.getDepth(pRoot.left)
diff=rHeight - lHeight
if (diff <=1 and diff >=-1):
return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
else:
return False
def getDepth(self,pRoot):
if not pRoot:
return 0
left = self.getDepth(pRoot.left)
right = self.getDepth(pRoot.right)
return max(left,right)+136.和为S的两个数,输出乘积最小的一组
# -*- coding:utf-8 -*-
class Solution:
def FindNumbersWithSum(self, array, tsum):
# write code here
if array==[] :
return []
start=0
end=len(array)-1
while (starttsum:
end-=1
if s 37.扑克牌顺子
# -*- coding:utf-8 -*-
class Solution:
def IsContinuous(self, numbers):
# write code here
if len(numbers)<5:
return False
minnum=14
maxnum=-1
num_dict={}
for i in numbers:
if i==0:
continue
if i not in num_dict:
num_dict[i]=0
num_dict[i]+=1
if num_dict[i]==2:
return False
if i > maxnum:
maxnum=i
if i < minnum:
minnum=i
if maxnum-minnum>=5:
return False
return True38.约瑟夫环
思路1:队列模拟
# -*- coding:utf-8 -*-
class Solution:
def LastRemaining_Solution(self, n, m):
# write code here
if m==0 and n==0:
return -1
q=[]
for i in range(n):
q.append(i)
while (len(q)>1):
for j in range(m-1):
q.append(q.pop(0))
q.pop(0)
left=q.pop()
return left
思路2:找规律
class Solution:
def LastRemaining_Solution(self, n, m):
if n < 1:
return -1
con = range(n)
final = -1
start = 0
while con:
k = (start + m - 1) % n
final = con.pop(k)
n -= 1
start = k
return final