【数据结构】关键路径

在有向图中，如果用顶点表示事件，弧表示活动，弧上的权值表示活动持续的时间，这样的活动称为边表示活动的网，简称AOE网（Activity On Edge）。通常可以用AOE网来估算工程的完成时间，他不仅表达了工程中各事件的先后关系，更可说明整个工程至少需要多少时间完成以及哪些活动是影响工程进度的关键活动。

在AOE网中：

源点：一个入度为零的事件

汇点：一个出度为零的事件

由于一个AOE网中某些活动可以并行地进行，所以完成的工程的最短时间是从源点到汇点最长路径的长度。相应地，从源点到汇点的最长路径称为AOE网的关键路径。

AOE网的创建以及求出各事件的最早发生时间和各事件的最晚允许开始时间

：活动  的最早开始时间

：活动最迟开始时间，这是在不推迟整个工程完成的前提下，活动  最迟必须开始的时间。

若某一活动  最早开始时间  等于这个活动的最迟开始时间 ，则说明  是一个关键活动。

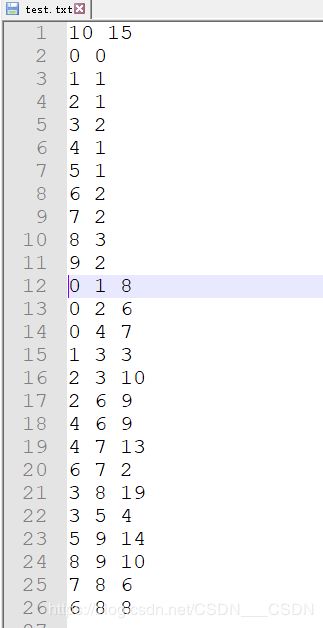
文件直接读取数据！！！！

#include 
#include 
#include 

const int M = 20;
int ve[M];//事件最早发生时间向量
int seq[M];//拓扑排序列向量
int vl[M];//事件最晚允许发生时间向量
int e[M];//活动的最早开始时间
int l[M];//活动最迟开始时间

typedef struct node//边结点类型定义
{
	int adjvex;
	int len;
	struct node *next;
}EdgeNode;

typedef struct de //带顶点入度的头节点定义
{
	EdgeNode *FirstEdge;
	char vertex;
	int id;
}vertexnode;

typedef struct 
{
	vertexnode adjlist[M];
	int n,e;
}AoeGraph;

void creat (AoeGraph *g)
{
	int i,j,k,len;
	EdgeNode *s;
	FILE *f;
	f=fopen("test.txt","r");
	fscanf(f,"%d%d",&g->n,&g->e);
	for(i=0;in;i++)
	{
		fscanf(f,"%1s %d",&g->adjlist[i].vertex,&g->adjlist[i].id);
		g->adjlist[i].FirstEdge=NULL;
	}
	for(k=0;ke;k++)
	{
		fscanf(f,"%d%d%d",&i,&j,&len);
		s=(EdgeNode*)malloc(sizeof(EdgeNode));
		s->len=len;
		s->adjvex=j;
		s->next=g->adjlist[i].FirstEdge;
		g->adjlist[i].FirstEdge=s;
	}
	return ;
}

void print(AoeGraph g)
{
	EdgeNode *p;
	int i;
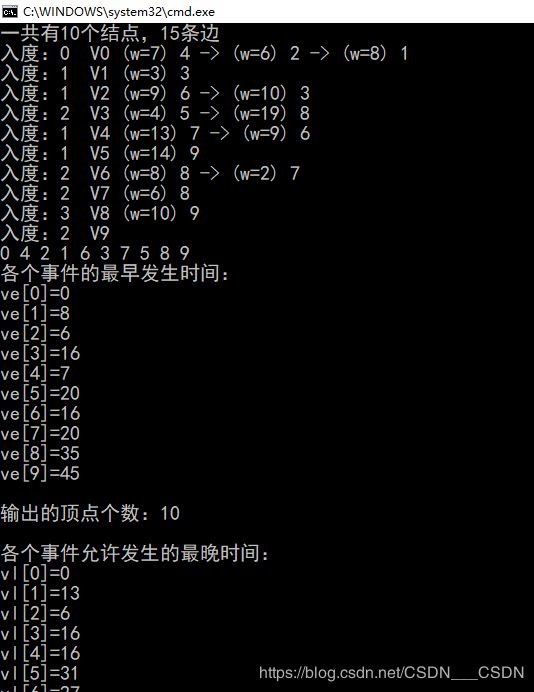
	printf("一共有%d个结点，%d条边\n",g.n,g.e);
	for(i=0;ilen,p->adjvex);
			if(p->next)
				printf(" -> ");
			p=p->next;
		}
		printf("\n");
	}
	return ;
}

//求每个事件最早发生的时间
int EarlistTime(AoeGraph gout)//返回输出的顶点个数
{
	int count=0,i,j,v,flag[M];
	int queue[M];
	int front = 0,rear = 0;
	EdgeNode *p;
	memset(ve,0,sizeof(ve));//初始化每个顶点最早开始时间是ve[i]=0;
	memset(flag,0,sizeof(flag));//访问标记初始化
	for(i=0;i< gout.n;i++)
	{
		if(gout.adjlist[i].id==0 && flag[i]==0)
		{
			queue[rear++]=i;
			flag[i]=1;
		}
	}
	while(front < rear)//队列不为空
	{
		v=queue[front++];//队首元出队
		printf("%c ",gout.adjlist[v].vertex);
		seq[count++]=v;//记录拓扑排序当前元素，计数器加一
		p=gout.adjlist[v].FirstEdge;
		while(p)
		{
			j=p->adjvex;
			if(--gout.adjlist[j].id==0 && flag[j]==0)//入度为0则将进队
			{
				queue[rear++]=j;
				flag[j]=1;
			}
			if(p->len+ve[v]>ve[j])
				ve[j]=ve[v]+p->len;
			p=p->next;
		}
	}
	printf("\n各个事件的最早发生时间：\n");
	for(i=0;i-1)//按照拓扑排序求各事件最晚时间
	{
		v=seq[k];
		p=gin.adjlist[v].FirstEdge;
		while(p)
		{
			j=p->adjvex;
			if(vl[j]-p->len < vl[v])
				vl[v]=vl[j]-p->len;
			p=p->next;
		}
		k--;
	}
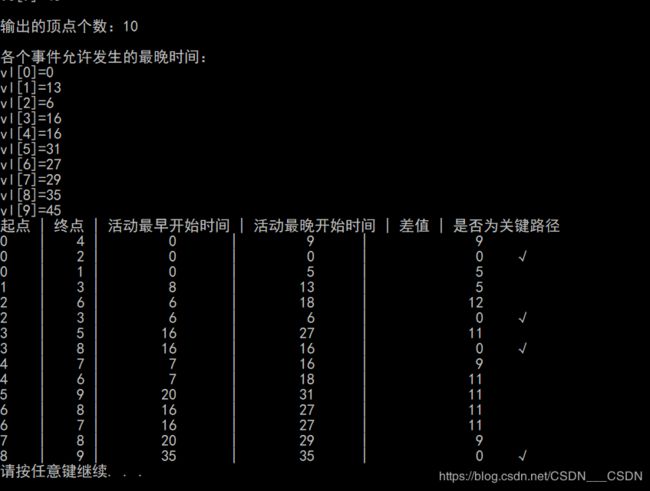
	printf("各个事件允许发生的最晚时间：\n");
	for(i=0;iadjvex;
			e[i]=ve[j];
			l[i]=vl[k]-p->len;
			printf("%c    |%5d |%10d        |%10d        |%5d |",g.adjlist[j].vertex,k,e[i],l[i],l[i]-e[i]);
			if(e[i]==l[i])
			{
				printf("    √\n");
			}
			else
			{
				printf("    \n");
			}
			printf("--------------------------------------------------------------------------\n");
			p=p->next;
		}
	}
}


int main ()
{
	AoeGraph g;
	creat(&g);
	print(g);
	printf("\n输出的顶点个数：%d\n\n",EarlistTime(g));
	LateTime(g);
	activity(g);
	return 0;
}