简版Word2vec的理解

一. 预备知识

1.1 哈夫曼树 （最优二叉树）

哈夫曼树 ：带权路径长度之和（WPL）最小的二叉树 。
WPL唯一，但哈夫曼树不唯一，左右子树可以交换。

权值越大的节点离根节点越近。
词频越大的词离根节点越近。
构造过程中，每两个节点都要进行一次合并。
因此，若叶子节点的个数为n,则构造的哈夫曼树中新增节点的个数为n-1。

哈夫曼编码：即满足前缀编码的条件，又能保证报文编码总长最短。
前缀编码：要求一个字符的编码不能是另一个字符编码的前缀。
约定：权值大的节点作为左孩子编码为1，权值小的节点作为右孩子编码为0。

1.2 词向量

两种表示方式
One hot representation：词向量维度大小为整个词汇表的大小，对于每个具体的词汇表中的词，将对应的位置置为1。
Dristributed representation：通过训练，将每个词都映射成一个固定长度的短向量。

二. 神经概率语言模型

输入层：2c个上下文词向量
投影层： 将2c个词向量拼接起来
隐藏层：有
输出层： y 维度为词汇表长度， 经过softmax 就得到每个单词的概率

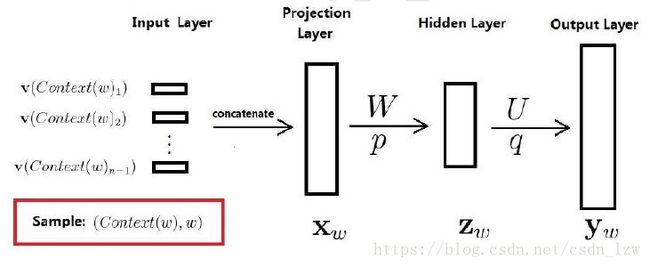
待学参数：
词向量 一般的DNN输入是已知的但是词向量作为输入也需要通过训练得到
神经网络参数：权值矩阵，阈值向量

三. 基于Hierarchical Softmax的word2vec

3.1 word2vec 模型：

word2vec 有两个模型
CBOW （Continuous Bag-of-Words）
Skip-gram
模型包括三层：输入，投影，输出
前者：已知当前词 wt w t 的上下文 wt−2,wt−1,wt+1,wt+2 w t − 2 , w t − 1 , w t + 1 , w t + 2 的前提下预测当前词 wt w t 。
后者：相反

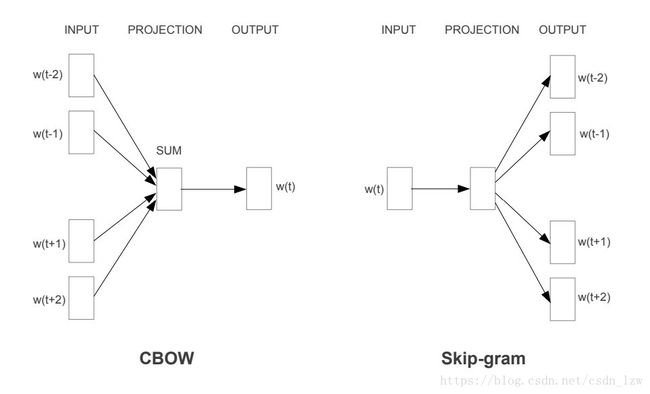
CBOW 目标函数 对数似然函数最大化

L=∑w∈Clogp(w|Context(w)) L = ∑ w ∈ C l o g p ( w | C o n t e x t ( w ) )

Skip-gram 目标函数

L=∑w∈Clogp(Context(w)|w) L = ∑ w ∈ C l o g p ( C o n t e x t ( w ) | w )

C C 表示语料库

3.2 基于Hierarchical Softmax的CBOW模型

输入层： 2c个词向量
投影层： 将2c个向量求和累加
隐藏层：无
输出层：一棵哈夫曼树，以语料库中出现的词当叶子节点，以个词频当权值构造出来的哈夫曼树。

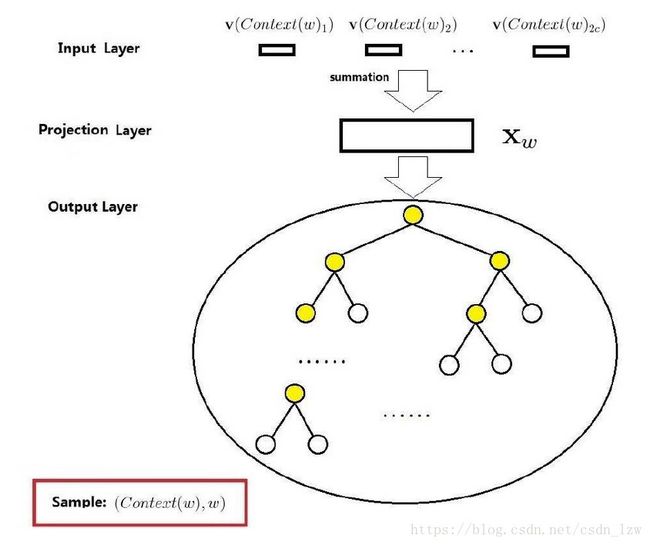
条件概率就可以通过路径累乘得到
从根到叶子节点对应着一条路径这个路径是唯一的，路径上的分支（每一个内部节点图中的黄色节点）就看作一次二分类，每一次分类就产生一个概率（用LR模型）。将概率乘起来就是所需的条件概率。
待求参数：每一内部节点就是一个LR，LR的参数 θ θ

σ(xTwθ)=11+e−xTwθ σ ( x w T θ ) = 1 1 + e − x w T θ

词向量也是要学的 xw x w 也是参数
似然函数最大化 ，梯度上升 得到更新公式。

∂L∂θ ∂ L ∂ θ

∂L∂xw ∂ L ∂ x w

最终的目标是要求词典中每个词的词向量。 xw x w 表示： context(w) c o n t e x t ( w ) 中各词词向量的累加，
利用 ∂L∂xw ∂ L ∂ x w 来对上下文词向量更新
CBOW 每次更新2c个词向量

四. 基于Negative Sampling（负采样）的word2vec

4.1 CBOW

CBOW中，已知词 w w 的上下文 context(w) c o n t e x t ( w ) ,需要预测 w w 。
因此，对于给定的 context(w) c o n t e x t ( w ) ，词 w w 就是一个正样本，其他词就是负样本。
w w 的负样本子集 NEG(w) N E G ( w )
目标函数：

g(w)=σ(xTwθw)∏u∈NEG(w)[1−σ(xTwθu)] g ( w ) = σ ( x w T θ w ) ∏ u ∈ N E G ( w ) [ 1 − σ ( x w T θ u ) ]

其中 σ(xTwθw) σ ( x w T θ w ) 表示当上下文为 context(w) c o n t e x t ( w ) 时，预测中心词为 w w 的概率。
σ(xTwθu)，u∈NEG(w) σ ( x w T θ u ) ， u ∈ N E G ( w ) 表示上下文为 context(w) c o n t e x t ( w ) 时，预测中心词为 u u 的概率。
希望最大化 σ(xTwθw) σ ( x w T θ w ) ，同时最小化所有的 σ(xTwθu) σ ( x w T θ u ) 。
对于语料库，目标函数

G=∏w∈Cg(w) G = ∏ w ∈ C g ( w )

同样，对 θ θ ， 对 xw x w 求导。

负采样算法

如果词汇表的大小为N,那么我们就将一段长度为1的线段分成N份，每份对应词汇表中的一个词。
当然每个词对应的线段长度是不一样的（非等距剖分），高频词对应的线段长，低频词对应的线段短。
高频词被选为负样本的概率大。

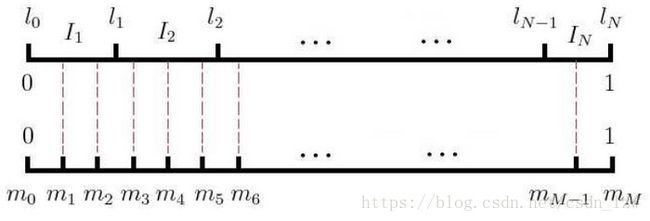
在采样前，我们将这段长度为1的线段划分成M等份（等距剖分），这里M>>N，这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。
如图m和I就建立了映射关系。
每次随机生成 [1,M-1] 间的随机整数，根据这个映射就得到样本。
如果碰巧选到自己就跳过。

参考文献：https://blog.csdn.net/itplus/article/details/37969519