POJ 1182 食物链(并查集） 详解

POJ 1182 食物链(并查集） 详解

分析

各元素之间是有关系的，所以我们要用一个数组val[]记录他们的类型。
然而他们具体是A/B/C中的谁是无法确定的，当然这些东西是无关紧要的，只要知道它们分为3类，就记为0，1，2。关系为0吃1,1吃2,2吃0。
为什么这么取？方便啊啊！比如判断 x 是否吃 y 等价判断 (val[x]+1)%3==val[y]

把所有能确定关系的元素放到一个集合，每个集合内的元素分3类（val[]=0，1，2 咯）。
为了方便，我们让根始终为第0类，即val[根]=0

如果我们要合并集合怎么办？比如我知道 x y是同一类，怎么合并呢？
为方便叙述，记G(x) 为x实在集合，G(x).i 为x实在集合的第i类别
首先我们要肯定一点G(x).i和G(y).i不是一个类别，所以合并时要更新一个集合的类别与另一个对应。
所以我们更新让val[G(y).i]=val[G(x).((i+1)%3)],即让G(y).i的每个元素的val=(i+1).
想法是美好的，然而我们不可能每次操作都由集合的一个元素推出所有元素然后修改他们的值，复杂度太大了，所以我们想办法优化。

我们还是从并查集压缩路径的过程入手吧
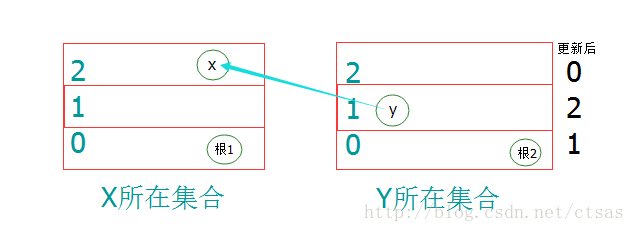
假设G(y)的每个元素都是指向根的，然后如再上图合并G(x)与G(y)：
par[find(y)]=find(x);//跟2指向了根1

之后我们如果查找G(y)的每个元素，比如find(y)，过程如下：
y -> 跟2 -> 根1
每个元素都是如此，都会经过跟2。那么我们能否利用这个特性来完成优化呢？答案是肯定的。直接看做法吧：

我们在合并G(x)与G(y)的同时更新val[根2]=val[x];然后查找G(y)的每个元素，比如find(y)。我们是可以通过更新后的val[跟2]推出val[y]应该是多少。
val[y]=(3+val[y]-val[跟2])%3;
做法的高明之处在于在你要查询的时候我再更新值，这也导致了后期调用val值的时候得先查询一次(笑)。

注意以上的结论多是在假设G(y)的每个元素都是指向根的下成立的，那么如果集合的高度大于1，怎么办？其实我们不难知道这个压缩路径的并查集如果查询了之后都直接指向根的，然而他没有，说明它还没更新，所以只要我们在find函数里面注意这个顺序问题就ok了。

如果是捕食关系，跟以上的合并是一样的，差别在于y的类型与x的下一个类型一致。

具体解法

• 如果输入1 x y
  
  • 如果x所在集合和y所在集合没有交集 那么合并集合
  • 如果x所在集合和y所在集合有交集 那么判断是否与已知矛盾 ans++
• 如果输入2 x y
  
  • 如果x所在集合和y所在集合没有交集 那么合并集合
  • 如果x所在集合和y所在集合有交集 那么判断是否与已知矛盾 ans++

代码

我把两种情况合并起来写了

#include
#define MAX_N 50010
int par[MAX_N],val[MAX_N];

void init(int n){
    for(int i=0;i<=n;i++) par[i]=i;
}
int find(int x){
    if(par[x]==x) return x;

    //注意递归顺序  理由和下面的详细注释同理 
    int t=find(par[x]);
    val[x]=(val[par[x]]+val[x])%3;
    return par[x]=t;
}

void unite(int op,int x,int y){
    int t=find(y);/*find(y) 的功能不止找 y 所在集合的根 还有更新 y -> 根 的所有关系 保证val[y] 是最新状态  
                    所以不能省略这句直接写 val[find(y)]=(2+op+val[x]-val[y])%3;*/ 
    val[t]=(2+op+val[x]-val[y])%3;
    par[t]=find(x);
}

int main()
{
    int n,m,x,y,op,ans=0;
    scanf("%d%d",&n,&m);
    init(n);
    while(m--){
        scanf("%d%d%d",&op,&x,&y);
        if(x>n||y>n){
            ans++;
            continue;
        }
        if(find(x)!=find(y)) unite(op,x,y);
        else if((val[x]+op-1)%3!=val[y]) ans++;
    }
    printf("%d\n",ans);
    return 0;
}

题目

食物链
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 66851 Accepted: 19727
Description

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是”1 X Y”，表示X和Y是同类。
第二种说法是”2 X Y”，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。
Input

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。
Output

只有一个整数，表示假话的数目。
Sample Input

100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
Sample Output

3

参考做法

http://www.cnblogs.com/kuangbin/archive/2013/04/02/2996358.html