SVM支持向量机原理及python实现

基本概念

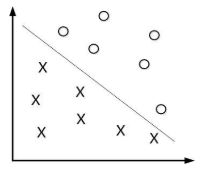
最简单的支持向量机是一个二分类的分类器。分类思想是给定一组包含正负样本的集合，然后找到一个超平面（可以是一维或者多维），来对正负样本进行分割。

该方法对于解决小样本，非线性，及高维模式识别中表现出许多的优势。

以下图的直线就是概念中的超平面，将样本划分为两个类别。在解决实际的多分类问题中可以转化为多个二分类问题。

其中的超平面方程由以下线性方程来描述。

​ $$g(x)=w^{T}x+b=0$$

其中$x$为样本的特征向量，$w^T$ 代表平面的法向量，而 $b$ 代表超平面的偏移量。

假设输入样本为 $x_0$，使得 $g(x_0)>0$ 的样本为正样本，反之为负样本，正负标签记为 ${+1, -1} $。

---

函数间隔

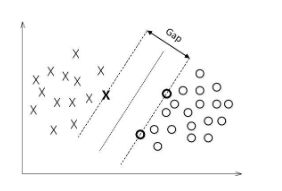
函数的间隔指的是正负样本点中到超平面的最近距离。对数据点进行分类，当超平面离数据点的间隔越大，分类的确信度越高。故当多个超平面的分类准确率一致时，我们要着重考虑最大间隔的分类器。

所以支持向量机的最终目标就是找到一个最大间隔的分类器。可以理解为一个约束优化问题，用以下式子来表示。

$$\begin{gathered} max\frac{r^{\ast }}{||w||} \\ subjectto{y}_i(w^T{x}_i+b)\ge r^{\ast } \end{gathered}$$

其中 $r^{\ast }$为函数间隔。

① 该方程并非凸函数求解，所以将方程转化为凸函数。转化为以下约束优化问题。

$$\begin{gathered} min\frac{1}{||w||} \\ subjectto{y}_i(w^T{x}_i+b)\ge r\ast \end{gathered}$$

转为凸函数以后，使用拉格朗日乘子法和KTT条件求解对偶问题。

②用拉格朗日乘子法和KKT条件求解最优值：

$$\min \frac{1}{2}||w|{|}^2$$

$$s.t.-y_i(w^T{x}_i+b)+1\le 0,i=1,2,..,m$$

整合成：

$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(-y_i(w^T{x}_i+b)+1)$$

推导：$\min f(x)=\min \max L(w,b,\alpha )\ge \max \min L(w,b,\alpha )$

根据KKT条件：

$$\frac{\partial }{\partial w}L(w,b,\alpha )=w-\sum {\alpha }_i{y}_i{x}_i=0,w=\sum {\alpha }_i{y}_i{x}_i$$

$$\frac{\partial }{\partial b}L(w,b,\alpha )=\sum {\alpha }_i{y}_i=0$$

带入$L(w,b,\alpha )$

$\min L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+{\sum }_{i=1}^m{\alpha }_i(-y_i(w^T{x}_i+b)+1)$

$=\frac{1}{2}{w}^{T}w-{\sum }_{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-b{\sum }_{i=1}^m{\alpha }_i{y}_i+{\sum }_{i=1}^m{\alpha }_i$

$=\frac{1}{2}{w}^T\sum {\alpha }_i{y}_i{x}_i-{\sum }_{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i+{\sum }_{i=1}^m{\alpha }_i$

$={\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i$

$={\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)$

再把max问题转成min问题：

$\max {\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)=\min \frac{1}{2}{\sum }_{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)-{\sum }_{i=1}^m{\alpha }_i$

$s.t.{\sum }_{i=1}^m{\alpha }_i{y}_i=0,$

${\alpha }_i\ge 0,i=1,2,...,m$

以上为SVM对偶问题的对偶形式

---

kernel

在低维空间计算获得高维空间的计算结果，也就是说计算结果满足高维（满足高维，才能说明高维下线性可分）。

soft margin & slack variable

引入松弛变量$\xi \ge 0$，对应数据点允许偏离的functional margin 的量。

目标函数：$\min \frac{1}{2}||w|{|}^2+C\sum {\xi }_{i}s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i$

对偶问题：

$$\max \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)=\min \frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)-\sum _{i=1}^m{\alpha }_i$$

$$s.t.C\ge {\alpha }_i\ge 0,i=1,2,...,m\sum _{i=1}^m{\alpha }_i{y}_i=0,$$

---

Sequential Minimal Optimization

首先定义特征到结果的输出函数：$u=w^{T}x+b$.

因为$w=\sum {\alpha }_i{y}_i{x}_i$

有$u=\sum y_i{\alpha }_{i}K(x_i,x)-b$

---

$\max {\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j<\varphi (x_i{)}^T,\varphi (x_j)>$

$s.t.{\sum }_{i=1}^m{\alpha }_i{y}_i=0,$

${\alpha }_i\ge 0,i=1,2,...,m$

---

参考资料：

[1] :Lagrange Multiplier and KKT

[2] :推导SVM

[3] :机器学习算法实践-支持向量机(SVM)算法原理

[4] :Python实现SVM

---

python 实现

以下是利用sklearn的一个简单实现。

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import  train_test_split
import matplotlib.pyplot as plt
%matplotlib inline

# data
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]

## 生成数据集并显示 
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()

数据集如上。

SVM实现如下：

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel
    
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0
        
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r
    
    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
    
        return 0
    
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
    
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        
        for i in index_list:
            if self._KKT(i):
                continue
            
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
        
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha      
    
    def fit(self, features, labels):
        self.init_args(features, labels)
        
        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()
            
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
                
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue
                
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b 
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b 
            
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
                
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'
            
    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
            
        return 1 if r > 0 else -1
    
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)
    
    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1)*self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w