瓦片地图(Tiled Map)系列文章:
斜45度瓦片地图(Staggered Tiled Map)里的简单数学
瓦片地图注意事项
前段时间在做游戏的地图编辑功能,我们是在一个斜45度视角的场景上,对地图上的建筑或装饰物进行添加、移动、移除等基本操作,而且位置的改变是以网格作为最小操作单位的。本渣是用Staggered Tiled Map实现的,与垂直视角的Tiled Map不同,斜45度视角处理起来相对麻烦些,这次就聊聊其中一些跟数学相关的有趣问题。
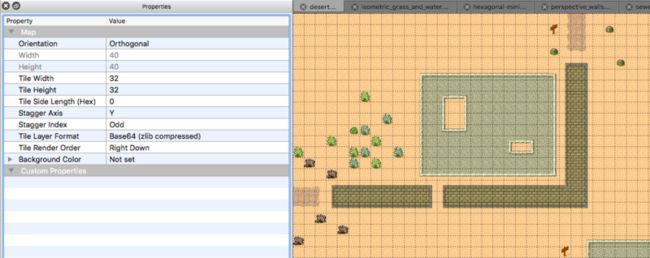
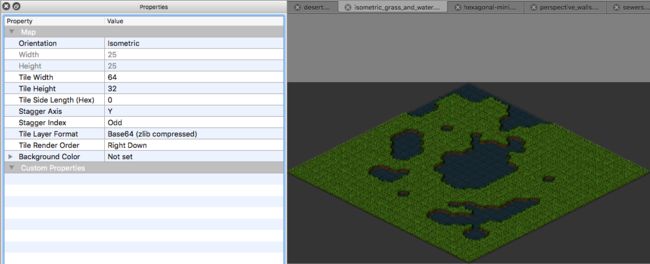
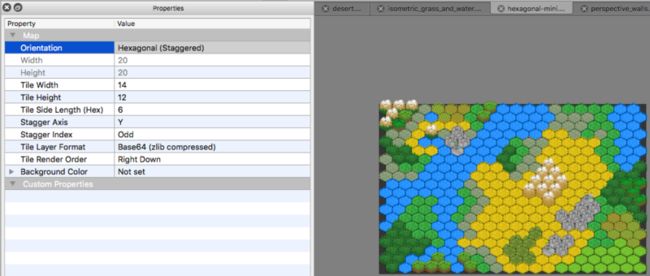
何为Staggered Tiled Map?
不解释,有图有真相XD
判断区域相交
地图编辑的一个基础功能便是判断当前被编辑的建筑或装饰物的位置的合法性。这种合法性检查主要有两方面:一是不能放置在地图上被禁止编辑的区域(例如地图上的河流、山坡),这可以通过在Tiled Map上在相应区域做上标记,判断建筑所在的区域是否有该标记就可以了;二是不能与其他建筑或装饰物重叠,这便是这里主要要讨论的问题了。
在实际做位置判断时,我们并非按照每个建筑或装饰物的图片实际轮廓,而是把它们都对应到Tiled Map上一块以网格线为边的区域上——在斜45度视角下,这样的区域就是一个平行四边形。因此,建筑或装饰物是否重叠的问题便转化为在Tiled Map上的两个平行四边形是否相交的问题。再做进一步简化,我们发现这其实只需要判断任一平行四边形的四个顶点的瓦片(tile)是否落在另一个平行四边形内部就可以了。
看到这里,你也许已经发现:这不就是中学里简单的代数问题吗?判断点是否在平行四边形内,只需要知道平行四边形四条边所在直线的方程和点的坐标,便迎刃而解。没错,Tiled Map里每一块瓦片区域有自己的坐标,我们只需要把一块瓦片的坐标当做点的坐标,直线方程和点的坐标就有了。但斜45度角Staggered Tiled Map的有趣之处在于,即便把瓦片当做点,得到的并不是一个常见的平面直角坐标系。
下面我们还是通过图片来看看Staggered Tiled Map的坐标:
为了方便起见,我们把向下作为y轴正方向,我们可以发现上面的坐标(x, y)有着如下规律:
-- columnNum表示列数
-- columnNum = 1, 2, 3, ...
x = (columnNum - 1) % 2
-- rowNum表示行数
-- rowNum = 1, 2, 3, ...
y = rowNum - 1看上去好像不复杂,但要列出直线方程呢?比如以下两种可作为平行四边形瓦片区域的边的直线:
一时半会懵逼了吧?使问题复杂的正是这些公式需要判断奇偶性,能不能把奇偶性判断拿掉呢?当然可以,做坐标转换就可以了,让我们先看一张直观的坐标转换结果图:
这相当于做了如下的坐标转换:
f[(x, y)] = (x * 2, y) if y mod 2 = 0
f[(x, y)] = (x * 2 + 1, y) if y mod 2 = 1合并成一条公式也就是:
f[(x, y)] = (x * 2 + y mod 2, y)现在是不是简单得多了?上面两条直线方程(因为这样的直线斜率是确定的,只需要知道直线上一点的坐标就可以确定直线方程)分别是:
-- linear equation of the row line containing the point of tileCoord
local function rowEquation(tileCoord)
return tileCoord.x * 2 + tileCoord.y % 2 + tileCoord.y
end-- linear equation of the column line containing the point of tileCoord
local function columnEquation(tileCoord)
return tileCoord.x * 2 + tileCoord.y % 2 - tileCoord.y
end这个时候你应该已经发现,我们可以用之前简单的代数问题解法来解决这一问题了:已知点的坐标tileCoord和一个区域region四个顶点的坐标(分别为region.top、region.bottom、region.left、region.right,事实上只需要知道其中两个点就可以了),判断点是否在区域内,只需要做不等式判断即可:
local function containsTile(region, tileCoord)
return (rowEquation(tileCoord) >= rowEquation(region.top))
and (rowEquation(tileCoord) <= rowEquation(region.bottom))
and (columnEquation(tileCoord) <= columnEquation(region.top))
and (columnEquation(tileCoord) >= columnEquation(region.bottom))你也许会问,为什么不直接定义一套方便计算的坐标系统?为何要用Staggered Tiled Map原有的坐标系统去做变换呢?这是因为前面所提到的做标记的非法编辑区域是采用原有的坐标系统的,采用同一套坐标系统加简单的坐标转换处理比起采用两套坐标系统,在实现上和维护上的成本更低。
遮挡关系
地图编辑的另一个基础需求是要处理好建筑及装饰物之间的遮挡关系。这个问题可以转化为建筑或装饰物的显示层级的排序。但是问题又来了,如何比较任意两个建筑或装饰物的显示先后顺序呢?特别是它们还有可能隔得很远,并没有显示上的重叠区域?
这个问题其实没有固定答案,本渣也只是根据我们系统的实际情况定了一套排序规则。在本渣的规则中,建筑或装饰物的显示层级只与它们对应的平行四边形区域有关。本渣用每一个的平行四边形左侧和右侧瓦片的坐标点得到一条直线,并把平行四边形对角线交点作为基准点。当比较两个建筑或装饰物的显示先后时,先判断二者平行四边形的宽度(两条相邻边的tile数量),短的求基准点,长的求直线。如果点在直线下方,则点所对应的建筑或装饰物在前方;反之则在后方。
当然,本渣这套规则实际能显示正确还有赖于美术大大们提供的建筑或装饰物图片资源的情况哈,如果建筑或装饰物的轮廓宽度超过它们的平行四边形区域,还是可能会出现显示奇怪的地方的。