机器学习之层次聚类及代码示例
一、层次聚类
层次聚类是无监督学习方法,可对给定的N个待聚类的样本进行层次的分类,直到某种条件(类的个数、类间的距离超过某个阈值)满足为止。
1、层次聚类的划分
对于层次聚类,可具体分为:
a. 凝聚的(agglomerative)层次聚类:
采用自底向上的策略:先将每个样本作为一个簇(类),然后不断地计算各个类之间的相似度/距离、并合并最相近的两个类成一个大类,直到某个终止条件满足为止。(可与哈夫曼编码算法作类比)
b. 分裂的(divisive)层次聚类:
采用自顶向下的策略,先将所有样本置于一个簇(类)中,然后根据一些原则逐渐细分为越来越小的类,直到某个终止条件满足为止。(可与决策树算法作类比)
2、类间的距离
在整个聚类的过程中,往往需要计算两个类的距离来进行凝聚/分隔的操作或者停止迭代的操作。判断两个类之间的距离/相似度可有以下三种方法:
a. SingleLinkage/Nearest-Neighbor:
取两个类中距离最近的两个样本的距离作为这两个类的距离。即最近两个样本之间的距离越小,这两个类的距离就越小。这种计算方法可能导致聚类的结果比较松散,且这种松散的效应会越来越大。比如当两个类总体上离得比较远,但却有对个别的点比较接近的情况。
b. CompleteLinkage:
取两个集合中距离最远的两个点的距离作为这两个类的距离,是SingleLinkage的反面极端情况。这种计算方法可能导致两个类因为个别的点而无法合并成一个类。
c. Average-linkage:
取两个类中的点两两的距离全部加在一起求平均值。这种方法得到的结果可能会受到个别点两两的距离的影响(偏大/偏小)。
d. Median-linkage / UCLUS:
median-linkage是average-linkage的一个变种,取两个类中的点两两的距离全部加在一起取中值作为两个类的距离。取中值与取均值相比,更加能够减少个人偏移样本对结果的干扰。
e. Centroids:
先分别计算出两个类的聚类中心,再取两个聚类中心的距离作为两个类的距离。
f. Ward’s method
假设先将两个类进行合并,得到合并后那个新cluster的均值点;再计算两个类中的每个点x到均值点的距离,再平方后加起来的结果即两个类的距离。
公式表示为 ![]() ,其中
,其中 ![]() 为合并后那个新cluster的中心点(均值点)
为合并后那个新cluster的中心点(均值点)
二、代码示例:
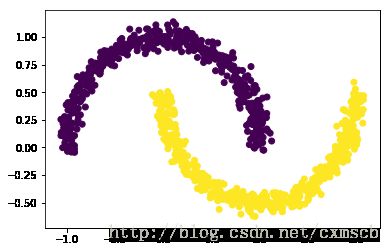
from sklearn.datasets.samples_generator import make_moonsX,y_true = make_moons(n_samples=1000,noise=0.05)import matplotlib.pyplot as pltplt.scatter(X[:,0],X[:,1],c=y_true)
plt.show()from sklearn.cluster import AgglomerativeClustering
import timet0 = time.time()
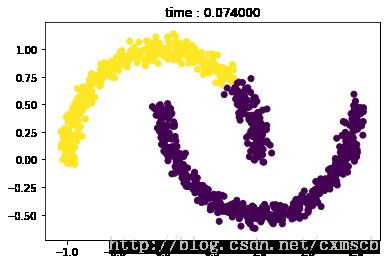
ward = AgglomerativeClustering(n_clusters=2,affinity='euclidean',linkage='ward',compute_full_tree='false').fit(X)
t = time.time() - t0plt.scatter(X[:, 0], X[:, 1], c=ward.labels_)
plt.title('time : %f'%t)
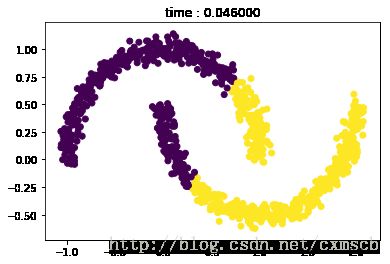
plt.show()from sklearn.cluster import KMeanst0 = time.time()
kmeans = KMeans(init = 'k-means++',n_clusters=2, random_state=8).fit(X)
t = time.time() - t0plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title('time : %f'%t)
plt.show()不难看出:基于距离的聚类算法(划分聚类、层次聚类),一般很难发现非凸形状的集合或者大小差别很大的集合。