iForest（Isolation Forest）孤立森林 异常检测

异常检测 (anomaly detection)

或者又被称为“离群点检测” (outlier detection)，是机器学习研究领域中跟现实紧密联系、有广泛应用需求的一类问题。但是，什么是异常，并没有标准答案，通常因具体应用场景而异。如果要给一个比较通用的定义，很多文献通常会引用 Hawkins 在文章开头那段话。很多后来者的说法，跟这个定义大同小异。这些定义虽然笼统，但其实暗含了认定“异常”的两个标准或者说假设：

1. 异常数据跟样本中大多数数据不太一样。

2. 异常数据在整体数据样本中占比比较小。

简介

Forest （Isolation Forest）孤立森林 是一个基于Ensemble的快速异常检测方法，具有线性时间复杂度和高精准度。其可以用于网络安全中的攻击检测，金融交易欺诈检测，疾病侦测，和噪声数据过滤等。

动机

目前学术界对异常的定义有很多种，iForest 适用与连续数据的异常检测，将异常定义为“容易被孤立的离群点——可以理解为分布稀疏且离密度高的群体较远的点。用统计学来解释，在数据空间里面，分布稀疏的区域表示数据发生在此区域的概率很低，因而可以认为落在这些区域里的数据是异常的。

iForest属于Non-parametric和unsupervised的方法，即不用定义数学模型也不需要有标记的训练。对于如何查找哪些点是否容易被孤立（isolated），

 

 

算法介绍

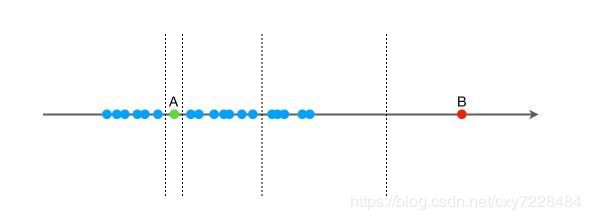
我们先用一个简单的例子来说明 Isolation Forest 的基本想法。假设现在有一组一维数据（如下图所示），我们要对这组数据进行随机切分，希望可以把点 A 和点 B 单独切分出来。具体的，我们先在最大值和最小值之间随机选择一个值 x，然后按照 =x 可以把数据分成左右两组。然后，在这两组数据中分别重复这个步骤，直到数据不可再分。显然，点 B 跟其他数据比较疏离，可能用很少的次数就可以把它切分出来；点 A 跟其他数据点聚在一起，可能需要更多的次数才能把它切分出来。

 

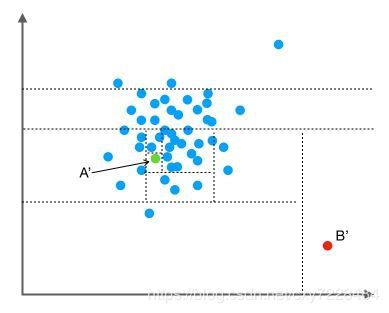
我们把数据从一维扩展到两维。同样的，我们沿着两个坐标轴进行随机切分，尝试把下图中的点A'和点B'分别切分出来。我们先随机选择一个特征维度，在这个特征的最大值和最小值之间随机选择一个值，按照跟特征值的大小关系将数据进行左右切分。然后，在左右两组数据中，我们重复上述步骤，再随机的按某个特征维度的取值把数据进行细分，直到无法细分，即：只剩下一个数据点，或者剩下的数据全部相同。跟先前的例子类似，直观上，点B'跟其他数据点比较疏离，可能只需要很少的几次操作就可以将它细分出来；点A'需要的切分次数可能会更多一些。

按照先前提到的关于“异常”的两个假设，一般情况下，在上面的例子中，点B和点B' 由于跟其他数据隔的比较远，会被认为是异常数据，而点A和点A' 会被认为是正常数据。直观上，异常数据由于跟其他数据点较为疏离，可能需要较少几次切分就可以将它们单独划分出来，而正常数据恰恰相反。这其实正是 Isolation Forest（IF）的核心概念。IF采用二叉树去对数据进行切分，数据点在二叉树中所处的深度反应了该条数据的“疏离”程度。整个算法大致可以分为两步：

1. 训练：抽取多个样本，构建多棵二叉树（Isolation Tree，即 iTree）；

2. 预测：综合多棵二叉树的结果，计算每个数据点的异常分值。

*训练*：构建一棵 iTree 时，先从全量数据中抽取一批样本，然后随机选择一个特征作为起始节点，并在该特征的最大值和最小值之间随机选择一个值，将样本中小于该取值的数据划到左分支，大于等于该取值的划到右分支。然后，在左右两个分支数据中，重复上述步骤，直到满足如下条件：

1. 数据不可再分，即：只包含一条数据，或者全部数据相同。

2. 二叉树达到限定的最大深度。

*预测：*计算数据 x 的异常分值时，先要估算它在每棵 iTree 中的路径长度（也可以叫深度）。具体的，先沿着一棵 iTree，从根节点开始按不同特征的取值从上往下，直到到达某叶子节点。假设 iTree 的训练样本中同样落在 x 所在叶子节点的样本数为 T.size，则数据 x 在这棵 iTree 上的路径长度 h(x)，可以用下面这个公式计算：

 

公式中，e 表示数据 x 从 iTree 的根节点到叶节点过程中经过的边的数目，C(T.size) 可以认为是一个修正值，它表示在一棵用 T.size 条样本数据构建的二叉树的平均路径长度。一般的，C(n) 的计算公式如下：

其中，H(n-1) 可用 ln(n-1)+0.5772156649 估算，这里的常数是欧拉常数。数据 x 最终的异常分值 Score(x) 综合了多棵 iTree 的结果：

公式中，E(h(x)) 表示数据 x 在多棵 iTree 的路径长度的均值， 表示单棵 iTree 的训练样本的样本数， 表示用条数据构建的二叉树的平均路径长度，它在这里主要用来做归一化。

从异常分值的公式看，如果数据 x 在多棵 iTree 中的平均路径长度越短，得分越接近 1，表明数据 x 越异常；如果数据 x 在多棵 iTree 中的平均路径长度越长，得分越接近 0，表示数据 x 越正常；如果数据 x 在多棵 iTree 中的平均路径长度接近整体均值，则打分会在 0.5 附近。

算法注意点

Isolation Forest 算法主要有两个参数：一个是二叉树的个数；另一个是训练单棵 iTree 时候抽取样本的数目。实验表明，当设定为 100 棵树，抽样样本数为 256 条时候，IF 在大多数情况下就已经可以取得不错的效果。这也体现了算法的简单、高效。

Isolation Forest 是无监督的异常检测算法，在实际应用时，并不需要黑白标签。需要注意的是：（1）如果训练样本中异常样本的比例比较高，违背了先前提到的异常检测的基本假设，可能最终的效果会受影响；（2）异常检测跟具体的应用场景紧密相关，算法检测出的“异常”不一定是我们实际想要的。比如，在识别虚假交易时，异常的交易未必就是虚假的交易。所以，在特征选择时，可能需要过滤不太相关的特征，以免识别出一些不太相关的“异常”。

 

 

代码块

# 调用模块
class sklearn.ensemble.IsolationForest（n_estimators = 100，max_samples ='auto'，contamination ='legacy'，max_features = 1.0，bootstrap = False，n_jobs = None，behavior ='old'，random_state = None，verbose = 0 ）

参数详情

n_estimators ： int，optional（默认值= 100）
整体中基本估算器的数量。

max_samples ： int或float，optional（default =“auto”）
从X中抽取的样本数量，用于训练每个基本估算器。
如果是int，则绘制max_samples样本。
如果是float，则绘制max_samples * X.shape [0]样本。
如果是“auto”，则max_samples = min（256，n_samples）。
如果max_samples大于提供的样本数，则所有样本将用于所有树（无采样）。

contamination ： float（0.，0.5），可选（默认值= 0.1）
数据集的污染量，即数据集中异常值的比例。在拟合时用于定义决策函数的阈值。如果是“自动”，则确定决策函数阈值，如原始论文中所示。

在版本0.20中更改：默认值contamination将从0.20更改为'auto'0.22。

max_features ： int或float，可选（默认值= 1.0）
从X绘制以训练每个基本估计器的特征数。

如果是int，则绘制max_features特征。
如果是float，则绘制max_features * X.shape [1]特征。
bootstrap ： boolean，optional（default = False）
如果为True，则单个树适合于通过替换采样的训练数据的随机子集。如果为假，则执行未更换的采样。

n_jobs ： int或None，可选（默认=无）
适合和预测并行运行的作业数。 None除非在joblib.parallel_backend上下文中，否则表示1 。 -1表示使用所有处理器。

random_state ： int，RandomState实例或None，可选（默认=无）
如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果没有，随机数生成器所使用的RandomState实例np.random。

verbose ： int，optional（默认值= 0）
控制树构建过程的详细程度。

实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest

# 获得一组有规律的数据

# 获得随机数生成器
rng = np.random.RandomState(42)

# 以给定的形状创建一个数组，数组元素来符合标准正态分布N(0,1)
X = 0.3 * rng.randn(100, 2)
# np.r是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等
X_train = np.r_[X + 1, X - 3, X - 5, X + 6]

# 再生成一组有规律的数据

# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 1, X - 3, X - 5, X + 6]

# 生成一组异常数据

# 随机生成-8-8之间(20,2)的出界数组
X_outliers = rng.uniform(low=-8, high=8, size=(20, 2))

# 导入模型

# 生成模型
clf = IsolationForest(max_samples=100*2)
clf.fit(X_train)
# 生成训练数据预测值
y_pred_train = clf.predict(X_train)
print('y_pred_train',y_pred_train)
# 生成测试数据预测值
y_pred_test = clf.predict(X_test)
print('y_pred_test',y_pred_test)
# 生成出界数据预测值
y_pred_outliers = clf.predict(X_outliers)

print('y_pred_outliers',y_pred_outliers)

得到结果  1 是正常值 -1是异常值

# 训练集里面的数据预测结果
y_pred_train [ 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1 -1  1  1  1  1  1  1  1 -1 -1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1 -1  1  1  1  1  1  1  1  1
  1  1 -1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1 -1 -1  1  1  1  1 -1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1
  1 -1  1  1  1  1  1  1  1  1  1  1  1 -1  1 -1  1  1  1 -1  1  1 -1  1
  1  1  1 -1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1 -1  1 -1  1 -1  1  1  1  1  1  1  1  1  1  1  1 -1  1 -1 -1  1  1  1
  1 -1 -1  1  1  1  1 -1  1  1  1  1  1 -1  1  1  1  1 -1  1  1 -1  1 -1
  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1]

# 测试集预测结果
y_pred_test [ 1  1  1  1 -1  1  1  1  1  1 -1  1  1  1  1  1  1 -1  1  1  1  1  1  1
 -1  1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1
  1  1 -1 -1  1  1  1  1  1 -1 -1  1  1  1 -1  1 -1  1  1  1  1  1 -1 -1
  1  1  1  1  1 -1 -1  1]

# 出界数据的预测结果
y_pred_outliers [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]