这一次的模拟赛一句话就是……考的不行……
对外宣称是NOIP的模拟赛，实际上难的……（可能因为我是蒟蒻的原因吧……）
一共6道题，55分（WTF？）
以下是题解……
鸥哨
【题解】
不难发现是一个组合数，于是就开始了一条不归路路——不断求阶乘，不断取模……最后妥妥地爆零！！！
为什么呢？——罪魁祸首就是因为一系列的不断取模……于是知道了一个神奇的“防爆”方法——逆元！
然后就可以通过逆元解决组合数爆炸的问题，最后不断更新答案就可以了！！！
什么是逆元？其实我也不清楚，但是并没有关系，只需要知道几件事情：
１、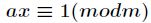
对于a、m，把同余方程中正整数x的最小值记作a模m的逆元；
２、逆元实际上就是用乘法代替除法；
３、用扩展欧几里得在算最大公约数的同时算出逆元（即：不定方程ax + my == 1的解x、y）；
嗯……大抵上就是这些了，不懂扩展欧几里得的话百度吧……不想写了
【代码】
#include
#include
#include
#include
#include
#include
#include
#include
【总结】
这道题考试的时候天真的想着简单的杨辉三角，n^2的算法，最后好像还打萎了，部分分都没有拿全
通过这道题大概了解了一些扩展欧几里得求逆元，总之调了很久，才A的
骨牌移动
【题解】
暴力枚，具体看代码
【代码】
#include
#include
#include
#include
#include
#include
#include
#include
【总结】
考试的时候写别的题去了，并没有写这道题，随便输了一个值，最后果断的爆零了
看了一眼题解后，瞬间后悔考试的时候的斜体顺序，直接用数组记录了每个骨牌的方向，直接爆搜就A了，但是需要注意边界，因为边界WA了一次
围圈
【题解】
一道贪心的题
对于圈中的每一个数i，如果他的l[i]、r[i]，满足l[i] > i且r[i] > i，那么一定是移除i，并且保留三个数中的最大数，显然是最优的，于是就会想到对于圈中每一个数进行排序，记录自己左边和右边的数，每一次把min(l[i], r[i]) - i加入ans即可
【代码】
#include
#include
#include
#include
#include
#include
#include
#include
【总结】
这道题考试的时候本来是接近正解了的，但是可能是排序的方式不对（或者打萎了吧）最后并没有得到预期分数
拿到题解后，简单的看了一下发现了排序的问题，在原代码上做了微调就A了
难解的集合
【题解】
又是一道求逆元的题，在第一中已经用过了扩展欧几里得，所以这道题用一用费马小定理
费马小定理具体的内容很混乱（反正我没怎么懂），但是核心部分很简单：假如p是质数，且gcd(a,p)=1，那么 a(p-1)≡1（mod p）
对于这道题，不难发现满足组合数，不妨假设f(x)指向p，即最终所有的元素的函数值的函数值等于p
如果已经满足l个f(x)指向了p，那么显然是求从n - 1个数中取l - 1数的组合数，因为数p以确定被取，所以n，l都要减去１，而对于剩下的n - l个数也要在l - 1个数中取，于是将两个方案数相乘加入答案即可，但注意此时的答案是针对一个数的，最后有n个数，所以不要忘记乘以n
【代码】
#include
#include
#include
#include
#include
#include
#include
#include
【总结】
对于这道题目，考试的时候并没有想到关于组合数、逆元、费马小定理之类一系列高大上的东西，于是就好不犹豫的打了一个n^n的表，最后20分
后面拿到题解后对于l分情况讨论不是很懂，于是就开始手玩（手玩是一个好东西啊），最后还是搞出来了，不过第一次用lemon测的时候ans忘记乘以n了，WA了一次，不过很快就调了出来
