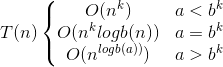Java-合并排序（归并排序）算法

基本思想：

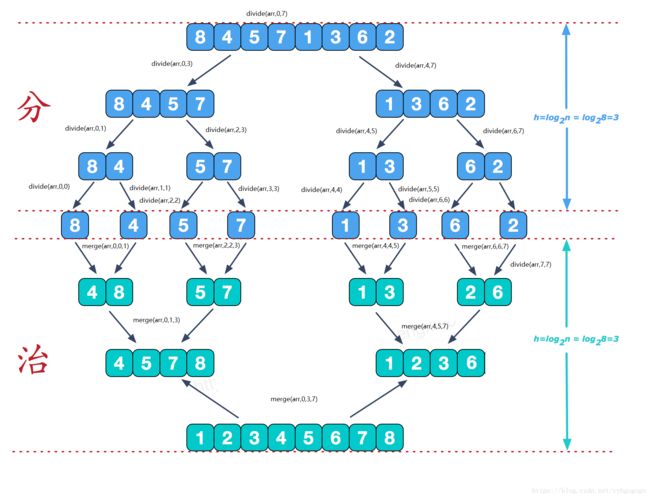
合并排序（归并排序）算法是用分治策略实现对n个元素进行排序的算法。其基本思想是：将待排序元素分成大小相同的2个集合，分别对2个集合进行排序，最终将排好序的子集合合并为所要求的排好序的集合。

分治策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)

 

 图解分析：

合并相邻有序子序列

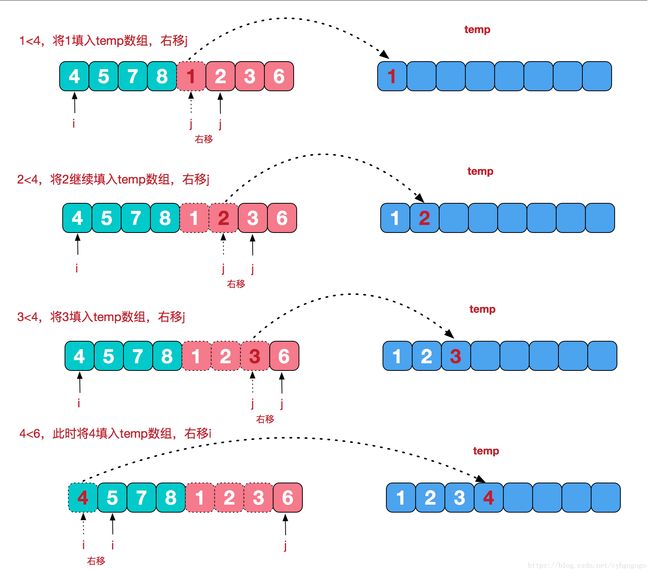
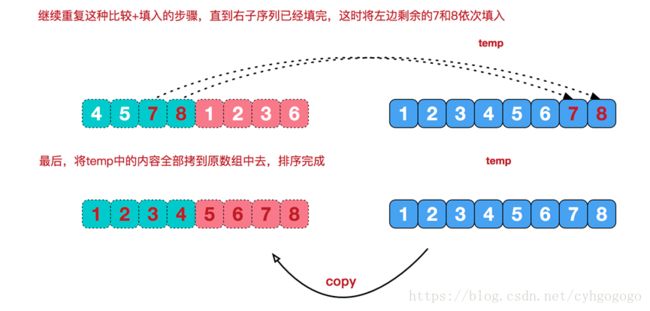
再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

递归分解步骤：

通过debug理清步骤：

divide(arr,0,7)
divide(arr,0,3)
divide(arr,0,1)
divide(arr,0,0)
divide(arr,1,1)
merge(arr,0,0,1)
divide(arr,2,3)
divide(arr,2,2)
divide(arr,3,3)
merge(arr,2,2,3)
divide(arr,4,7)
divide(arr,4,5)
divide(arr,4,4)
divide(arr,5,5)
merge(arr,4,4,5)
divide(arr,6,7)
divide(arr,6,6)
divide(arr,7,7)
merge(arr,6,6,7)
merge(arr,0,1,3)
merge(arr,4,5,7)
merge(arr,0,3,7)
 

代码实现

package SortType2;

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args)
    {
        int[] arr={8,4,5,7,1,3,6,2};
        createArray(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void createArray(int[] arr)
    //在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
    {
        int[] temp=new int[arr.length];
        divide(arr,0,arr.length-1,temp);
    }

    public static void divide(int[] arr,int left,int right,int[] temp)
    {
        if(left

 

时间复杂度

合并排序先将待排序元素分成大小一致的2个子集合，分别对2个子集合排序，最终合并2个排好序的数组段到新的数组temp中，然后copy数组回原来的数组arr中。

合并排序算法对n个元素进行排序，在最坏情况下所需的计算时间T(n)满足：

根据公式：

解次递归方程可知  a=2,b=2,k=1 即T(n)=O(nlogn)