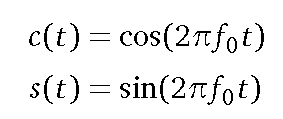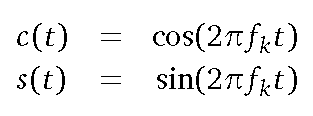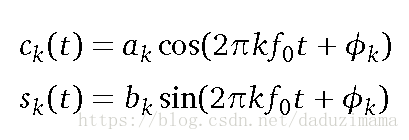周期信号的三角函数表示 (三角函数的性质和三角波的合成)
三角函数的性质
一系列三角函数谐波(harmonic sinusoids)是傅里叶分析的基石,我们可以用这些不同频率的谐波构建各种各样的信号/波形。
谐波(harmonics):
现在我们选择一个频率为f0的任意频率(arbitrary frequency)的正弦/余弦函数为基波(fundamental frequency)。则有一系列的基于该波的谐波(harmonics),这些谐波的频率都是基波的整数倍,例如,2f0, 3f0, 4f0, 5f0......kf0。
频率为任意频率f0的基波(一对正弦和余弦):
基于该基波的谐波分量fk = k*f0,k是任意整数:
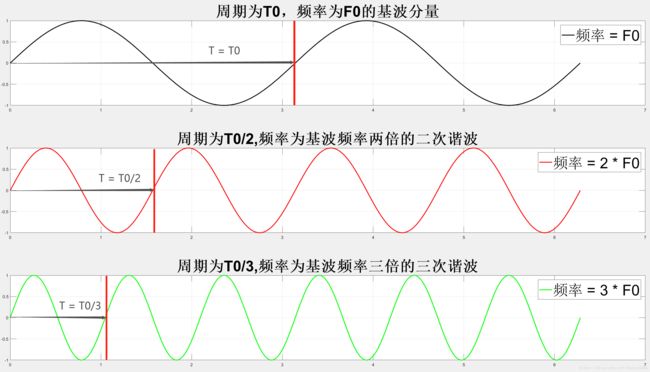
下图是频率为任意频率f0的基波及其谐波,周期逐级以整数倍递减,频率逐级以整数倍增加。
上图是频率为任意频率f0的基波及其谐波,周期逐级以整数倍递减,频率逐级以整数倍增加。
————————————————————————————————————————————————————
下面我们用另外一种方式来重新表示谐波,如下:
之前我们只是通过不同的频率或周期来表示不同的谐波,现在我们还能通过改变振幅(amplitude)和相位(phase)来定义不同的谐波。
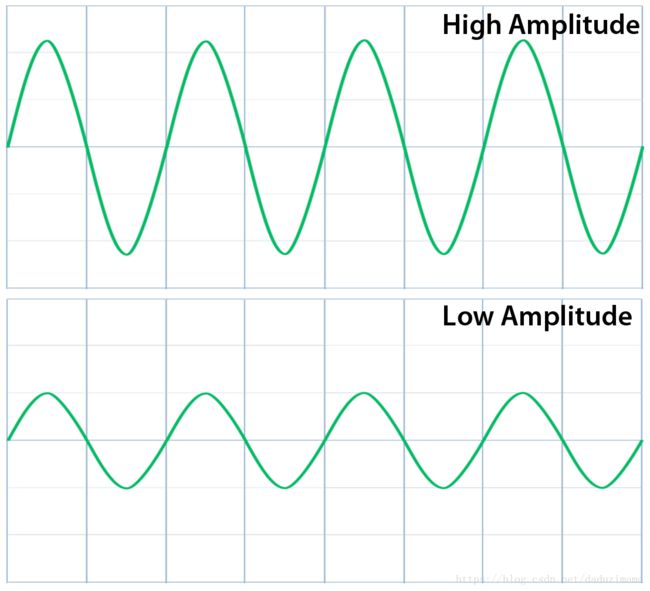
幅度(amplitude):
波的幅度就是信号中高于或低于信号均值的值,幅度可以是正值或负值。如果一个余弦函数的表达式为:a cos(wt),则该余弦曲线的最大值(+1)和最小值(-1)由系数a进行缩放。波形的最高峰值不会超过a,这个系数被称为波的幅度。在上面的两个等式中,ak和bk都是是波的幅度。
相位(phase):
相位可以理解成波形的起始位置,也可以理解成整个波形的整体移动。例如一个正弦波,当相位为0时,(即,无位移的情况下)他在0点的值是0。若发生了四分之一个周期的位移,即,90度的位移,则他在0点的值是正1。
上图中的一艘军舰遭遇了叠加着三种不同波长/不同频率海浪的拍打!当这些海浪由于相位不同,大部分能量相互抵消,所以大部分时候的海面风平浪静。当这些海浪的相位达到一种相互增强的情况下时,则最终会叠加成一个巨大的海浪(如上图中虚线)。是否会形成这种巨浪取决于这些分量的相对相位!
正交(orthogonality):
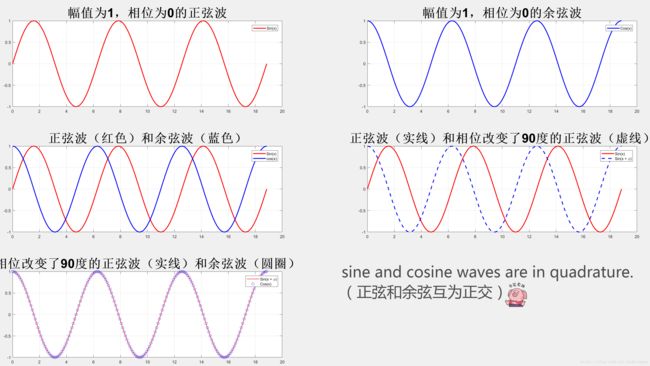
正弦波和余弦波正好差了π/2个相位,即90度。若有两个信号的相位相差-90度或+90度时,则这两个信号被视为是正交的,因此,正弦波和余弦波是相互正交的。
例如,下图中最后一图发生了90度移位的正弦波和余弦波正好重合。
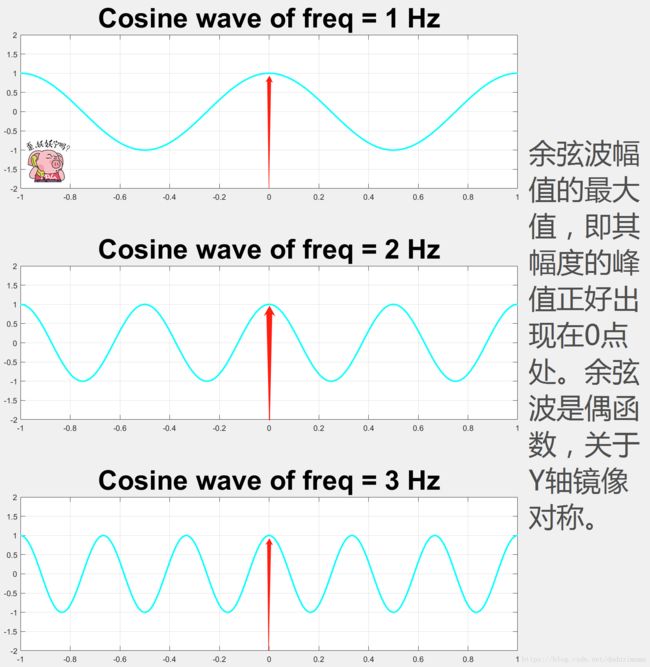
余弦波总是在0点(t = 0)处达到其峰值/最大值,且在此处的相位为π/2。正弦波,不论其频率为多少,在0点(t = 0)处总是为0,且此处的相位为0。因此,不管把多少任意频率,任意幅度的正弦波加在一起,最终的波形在0点处一定还是0。同理,不论把多少各种各样的余弦波加在一起,最终在0点的幅度总不是0。
用不同频率的三角波合成信号
谐波信号的叠加(只改变频率):
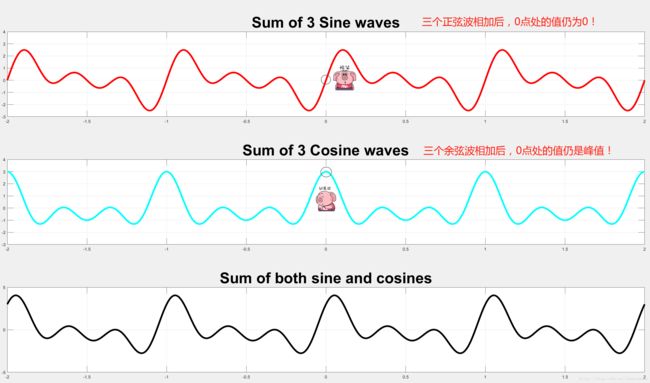
下面我们把上图中,幅度相同,0相位,不同频率的三个正弦波和三个余弦波加在一起。由下图中的实验结果知,三个正弦波/奇函数相加还是奇函数,并且在0点处的值还是0,关于原点中心对称。三个余弦波/偶函数相加的结果还是偶函数,并且在0点处的值还是峰值,关于Y轴镜像对称。最后一幅图是把正弦函数和余弦函数的和相加后的结果,这是信号合成的基础。
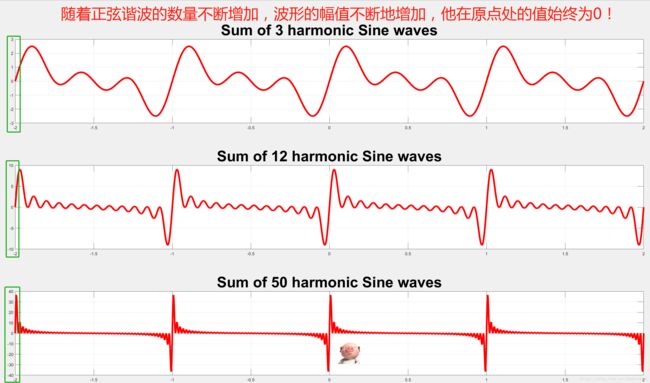
上图中的信号合成是用三个整数倍于基波频率f0的正弦谐波和余弦谐波的叠加而成的,请大家回忆一下,本文中一开始讲的基波频率整数倍的谐波,f0, 2f0, 3f0, 4f0.......kf0。上面只是用了3-6个谐波来合成新波形,并且不改变幅度和相位。接下来我们仍旧不改变谐波的幅度和相位,而是增加谐波的数量(增加到12,50个,乃至更多)来合成新的信号。
正弦谐波的叠加(只改变频率):
余弦谐波的叠加(只改变频率):
注意:我专门用黑框标注的幅度的变换。
正弦+余弦谐波的叠加,并取绝对值(只改变频率):
用无穷多个相同幅度,0相位的,不同频率的正弦和余弦的谐波叠加并取绝对值,最终会合成一个冲击串信号!
就目前来看,如果只是改变三角函数的频率能够合成的波形似乎非常有限。目前我们只是合成信号处理中最常见的冲击串和Sinc函数。那么其他的常见信号又是怎么用三角函数合成的呢?例如,方波,锯齿波,随机信号,等等。
预知后事如何,请见下回分解。
《圣经》约翰福音 12章:25 ------ 爱惜自己生命的,就失丧生命;在这世上恨恶自己生命的,就要保守生命到永生。
*配图与本文无关*