算法-分治法非常典型的应用之归并排序模拟与分析

归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列。

排序过程

归并排序的算法我们通常用递归实现，先把待排序区间[start,end]以中点二分，接着把左边子区间排序，再把右边子区间排序，这是分解的过程。最后把左区间和右区间用一次归并操作合并成有序的区间[start,end]，这是治理的过程。如何归并呢？ 简单来说两个指针分别指向待归并的数组，选出较小的，放到第三个指针控制的临时数组中。

实现代码

主题框架代码如下，见代码注释。

         /// 

        /// 主题框架
        /// 
        private void divideMerge(int[] unsort, int start, int end, int[] sort)
        {
            if (start < end)
            {
                int middle = (start + end) >> 1;
                //对前半部分归并排序
                divideMerge(unsort, start, middle, sort); 
                //对后半部分归并排序
                divideMerge(unsort, middle + 1, end, sort); 
                //此时，前、后半部分已经是有序序列，对它们实行二路归并
                merge(unsort, start, middle, end, sort);
            }

        }

调用的二路归并方法merge的实现代码如下，要特别注意临界值，此处pe为最大索引值，而不是元素个数，注意此处。

        /// 

        /// 合并算法
        /// 
        /// 无序数组
        /// 第1部分的起始位置
        /// 第1部分的结束位置
        /// 第2部分的结束位置
        /// 
        private void merge(int[] unsort, int ps, int pm, int pe, int[] sort)
        {
            int i = ps; //第一部分的取值范围为[ps,pm]
            int j = pm+1; //第二部分的取值范围为[pm+1,pe]

            int sortCount = 0;

            while (i <= pm && j <= pe)
            {
                if (unsort[i] < unsort[j])
                    sort[sortCount++] = unsort[i++];
                else
                    sort[sortCount++] = unsort[j++];
            }

            while (i <= pm)
                sort[sortCount++] = unsort[i++];

            while (j <= pe)
                sort[sortCount++] = unsort[j++];

            for (int sortIndex = 0; sortIndex < sortCount; sortIndex++)
                unsort[ps + sortIndex] = sort[sortIndex];

        }

封装了一个排序类，见下，提供的API有2个，

1. 归并排序接口MergeSort()
2. 构造函数，构造无序数组

    public class CMergeSort
    {
        private int[] _unsortArray;

        /// 

        /// 构造函数
        /// 
        /// 
        public CMergeSort(int[] unsortArray)
        {
            _unsortArray = unsortArray;
        }

        /// 

        /// 归并排序接口
        /// 
        /// 
        public int[] MergeSort()
        {
            int maxIndex = _unsortArray.GetUpperBound(0);
            int[] sort = new int[maxIndex + 1];
            divideMerge(_unsortArray, 0, maxIndex, sort);
            return sort;
        }
  }

客户端调用

客户端调用刚才写好的对象，对无序数组a实行归并排序。

        static void Main(string[] args)
        {
            int[] a = new int[] { 9,7,10,6,3,5,2,7,9};
            var merge = new CMergeSort(a);
            int[] sortArray = merge.MergeSort();

            Console.Read();
        }

记录了归并排序的过程，对此进行了结果分析。

结果分析

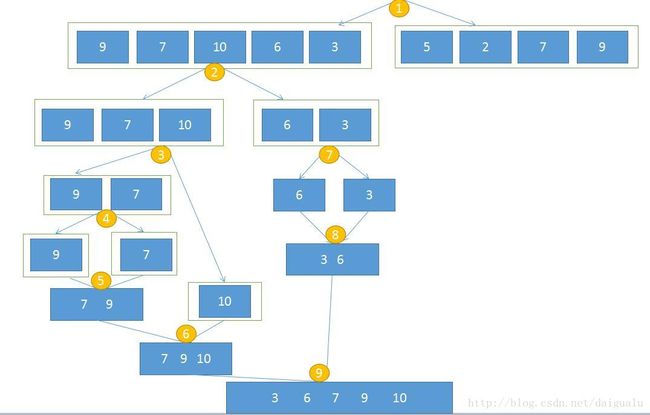
对数组的{ 9,7,10,6,3,5,2,7,9}的归并排序过程如下，

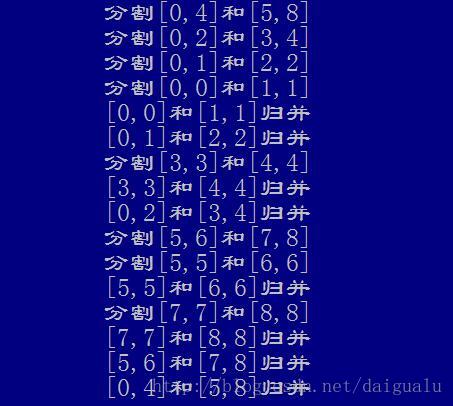
归并排序过程的前半部分，过程示意图见下，从图中可见，步骤1，2，3，4一直分割区间，等到步骤5时，左右区间长度都为1，此时发生一次归并，结果再与另一个区间长度为1的归并，即步骤6；步骤7分割，步骤8归并，步骤9归并后前半部分合并结束；
后半部分过程与前半部分归并一致，不再详述。

源码下载

http://download.csdn.net/detail/daigualu/9799598